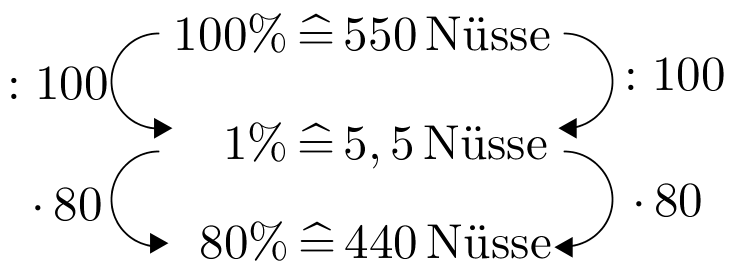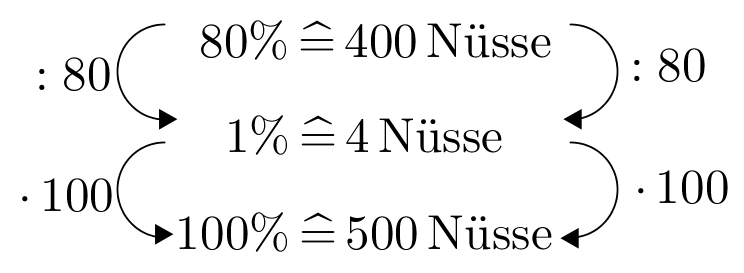Ein Eichhörnchen braucht im Winter 400 Nüsse. Es hat im Herbst 550 Nüsse vergraben. Im Winter findet es von den im Herbst vergrabenen Nüssen wieder.
Kommt es über den Winter?
Wie viele Nüsse muss das Eichhörnchen dafür mindestens vergraben?
Nüsse
WICHTIG: Damit alle Bilder und Formeln gedruckt werden, scrolle bitte einmal bis zum Ende der Seite BEVOR du diesen Dialog öffnest. Vielen Dank!
🎓 Ui, fast schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.
