Der Marketingchef einer Handelskette plant eine Werbeaktion, bei der ein Kunde die Höhe des Rabatts bei seinem Einkauf durch zweimaliges Drehen an einem Glücksrad selbst bestimmen kann. Das Glücksrad hat zwei Sektoren, die mit den Zahlen 5 bzw. 2 beschriftet sind (vgl. Abbildung). Der Rabatt in Prozent errechnet sich als Produkt der beiden Zahlen, die der Kunde bei zweimaligem Drehen am Glücksrad erzielt.
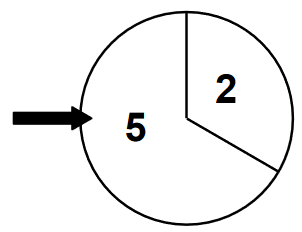
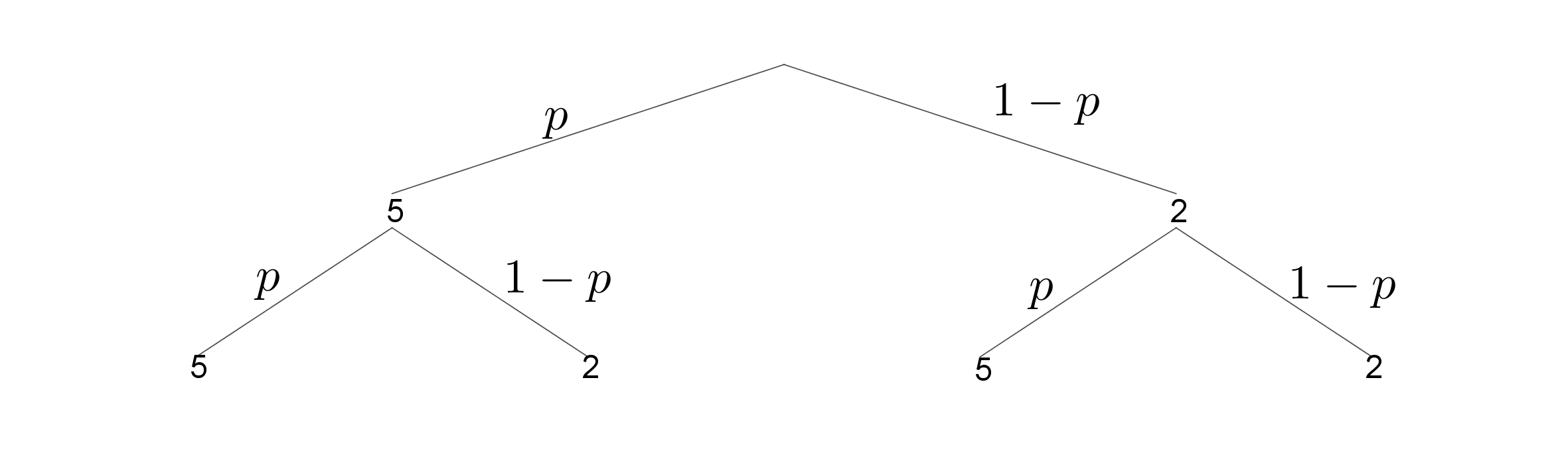
Die Zufallsgröße beschreibt die Höhe dieses Rabatts in Prozent, kann also die Werte 4, 10 oder 25 annehmen. Die Zahl 5 wird beim Drehen des Glücksrads mit der Wahrscheinlichkeit p erzielt. Vereinfachend soll davon ausgegangen werden, dass jeder Kunde genau einen Einkauf tätigt und auch tatsächlich am Glücksrad dreht.
Ermitteln Sie mithilfe eines Baumdiagramms die Wahrscheinlichkeit dafür, dass ein Kunde bei seinem Einkauf einen Rabatt von erhält. (3 BE)
Zeigen Sie, dass für den Erwartungswert der Zufallsgröße gilt: (3 BE).
Die Geschäftsführung will im Mittel für einen Einkauf einen Rabatt von gewähren. Berechnen Sie für diese Vorgabe den Wert der Wahrscheinlichkeit . (3 BE)
Die Wahrscheinlichkeit, dass ein Kunde bei seinem Einkauf den niedrigsten Rabatt erhält, beträgt . Bestimmen Sie, wie viele Kunden mindestens an dem Glücksrad drehen müssen, damit mit einer Wahrscheinlichkeit von mehr als mindestens einer der Kunden den niedrigsten Rabatt erhält. (4 BE)