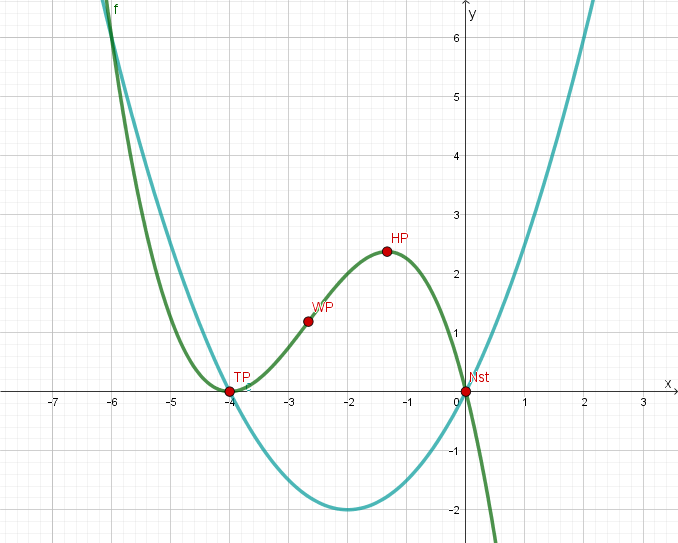🎓 Ui, fast schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.
Springe zum Inhalt oder Footer
SerloDie freie Lernplattform
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.

Der Graph GpG_p der quadratischen Funktion pp enthält die Punkte A(−6∣6)A(-6|6), B(−2∣−2)B(-2|-2) und C(1∣2,5)C(1| 2{,}5).

  1. Bestimmen Sie den Funktionsterm p(x)p(x). (7 BE)

    [Mögliches Ergebnis: p(x)=12(x2+4x)p(x)=\frac12(x^2+4x)]

  2. Zeichnen Sie den Graphen GpG_p im Bereich −6≤x≤1-6\le x\le 1 in das vorhandene Koordinatensystem ein. (2 BE)

  3. Die Graphen GfG_f und GpG_p schließen insgesamt zwei endliche Flächenstücke ein. Markieren Sie im vorhandenen Koordinatensystem das weiter links gelegene und berechnen Sie die Maßzahl seines Flächeninhalts. Die ganzzahligen Integrationsgrenzen können der Zeichnung entnommen werden. (6 BE)