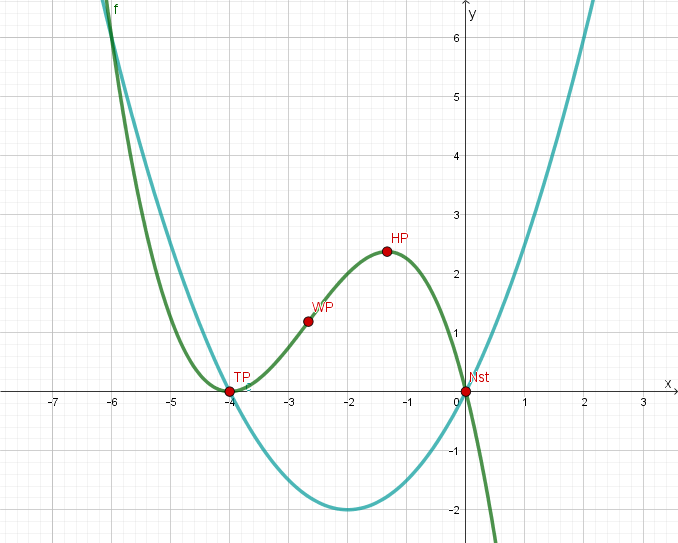A I
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
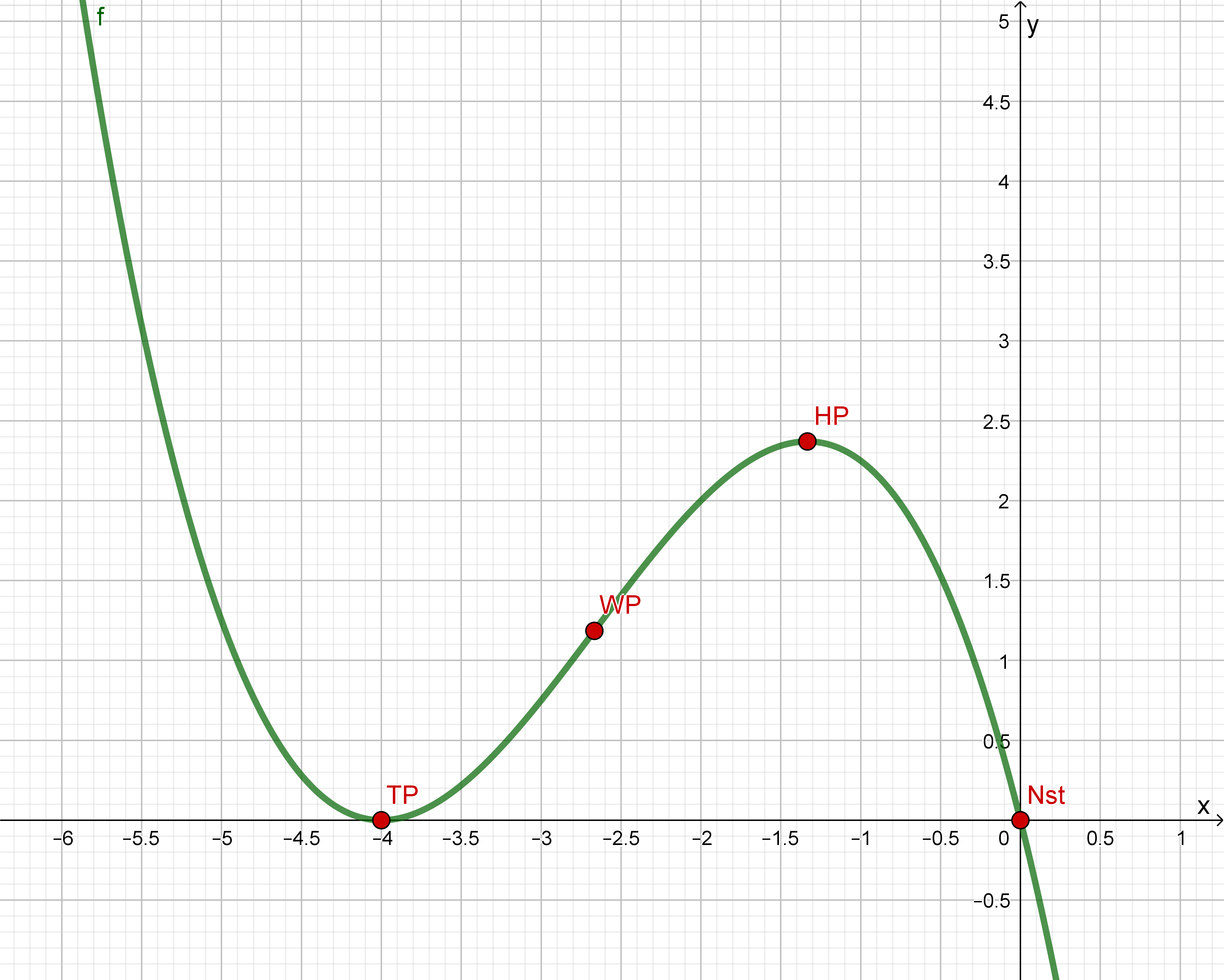
Gegeben ist die Funktion mit . Der Graph wird mit bezeichnet.
Ermitteln Sie sämtliche Nullstellen der Funktion mit jeweiliger Vielfachheit. (4 BE)
Bestimmen Sie die maximalen Monotonieintervalle sowie Art und Koordinaten der relativen Extrempunkte des Graphen . (8 BE)
Berechnen Sie die maximale positive Steigung des Graphen . (5 BE)
Zeichnen Sie den Graphen im Bereich unter Kennzeichnung bisheriger Ergebnisse in ein kartesisches Koordinatensystem. Maßstab: . (4 BE)
- 2
Der Graph der quadratischen Funktion enthält die Punkte , und .
Bestimmen Sie den Funktionsterm . (7 BE)
[Mögliches Ergebnis: ]
Zeichnen Sie den Graphen im Bereich in das vorhandene Koordinatensystem ein. (2 BE)
Die Graphen und schließen insgesamt zwei endliche Flächenstücke ein. Markieren Sie im vorhandenen Koordinatensystem das weiter links gelegene und berechnen Sie die Maßzahl seines Flächeninhalts. Die ganzzahligen Integrationsgrenzen können der Zeichnung entnommen werden. (6 BE)
- 3
Gegeben sind die reellen Funktionen mit und .
Bestimmen Sie Anzahl und Lage der Nullstellen der Funktion in Abhängigkeit von t. (7 BE)
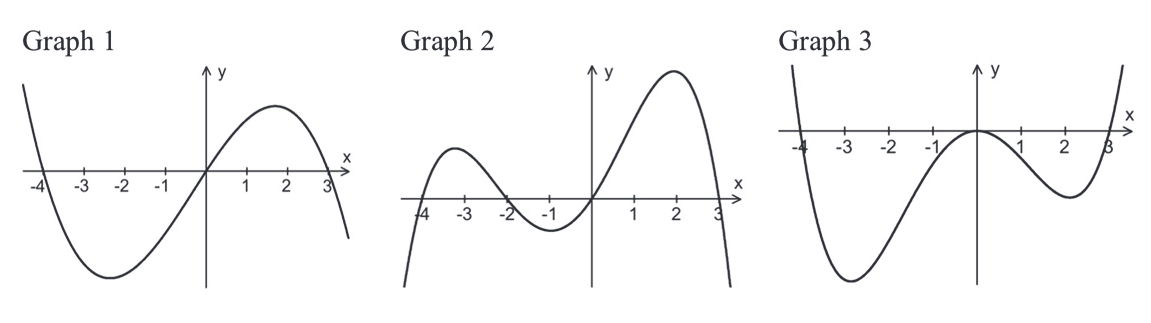
Begründen Sie, welche der im Folgenden dargestellten Graphen zur Funktionenschar gehören können und welche nicht. Begründen Sie jeweils Ihre Entscheidung mithilfe der ganzzahligen Nullstellen und ggf. des Grenzverhaltens bzw. des Leitkoeffizienten.
Geben Sie für den Fall, dass der Graph zur Funktionenschar gehört, den zutreffenden Wert von t an. (6 BE)
- 4
4.0 Ein Planschbecken soll entsprechend folgender Skizze hergestellt werden, wobei der Boden und die Wand luftgefüllte Hohlkammern mit einer Dicke von 10 cm sind. Die Summe aus Radius R und Höhe h soll konstant 90 cm betragen.
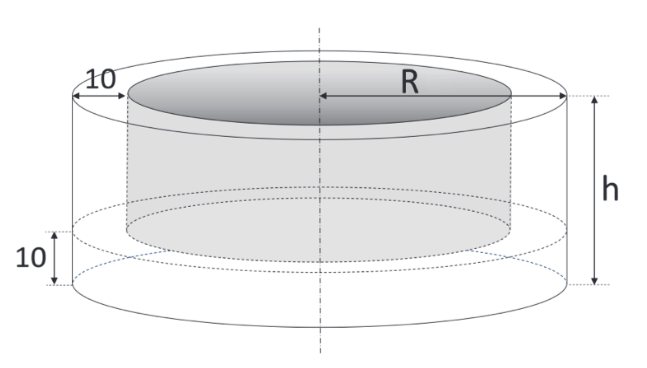
4.1 Stellen Sie eine Gleichung der Funktion V auf, welche die Maßzahl des Volumens des mit Luft gefüllten Teils des Planschbeckens in Abhängigkeit von R beschreibt. (6 BE)
[Mögliches Ergebnis: ]
4.2 Mit der Vorgabe soll die Funktion den absolut größten Wert annehmen. Berechnen Sie für diesen Fall die maximale Füllhöhe des Planschbeckens. (5 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?