Aufgabe B2
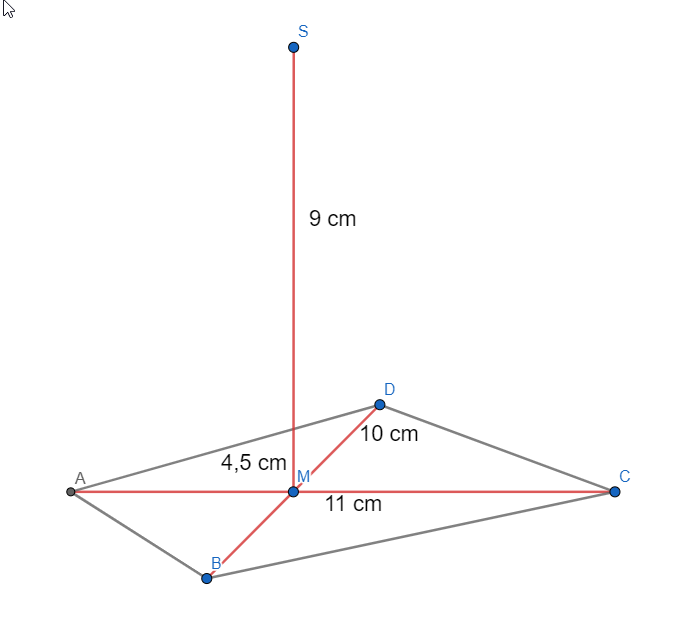
Die Diagonalen und des Drachenvierecks schneiden sich im Punkt . Das Drachenviereck ist die Grundfläche der Pyramide mit der Spitze und der Höhe .
Es gilt: cm; cm; cm; cm.
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Zeichnen Sie das Schrägbild der Pyramide , wobei auf der Schrägbildachse und der Punkt links vom Punkt liegen soll.
Für die Zeichnung gilt: und .
Berechnen Sie sodann das Maß des Winkels . [Ergebnis: ] (3 P)
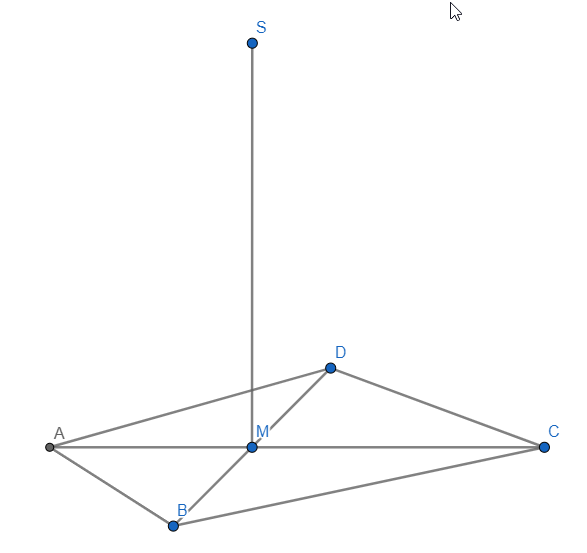
Punkte liegen auf der Strecke Die Winkel haben das Maß mit . Die Punkte sind zusammen mit den Punkten und die Eckpunkte von Dreiecken .
Zeichnen Sie die Strecke sowie das Dreieck für in das Schrägbild zu 2a) ein.
Zeigen Sie sodann, dass für die Länge der Strecken in Abhängigkeit von gilt: cm. (3 P)
Das Dreieck ist gleichseitig.
Berechnen Sie den zugehörigen Wert für . (3 P)
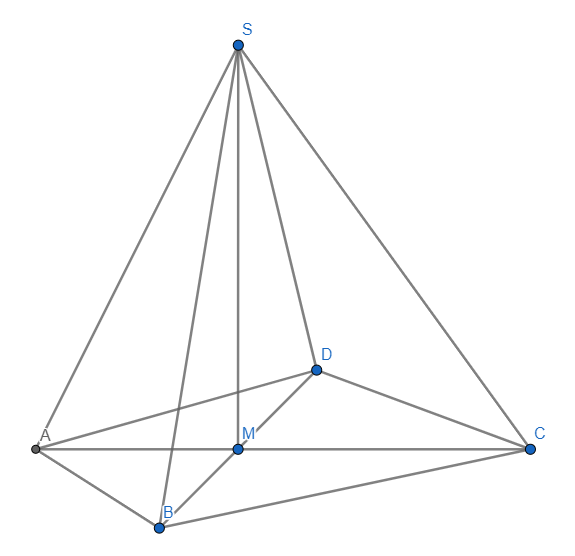
°Die Pyramiden haben die Grundfläche und die Spitzen . Die Höhenfußpunkte der Pyramiden liegen auf der Strecke .
Zeichnen Sie die Höhe in das Schrägbild zu ein.
Berechnen Sie sodann das Volumen der Pyramiden in Abhängigkeit von .
[Zwischenergebnis: ] cm (3 P)
Die Pyramiden und haben das gleiche Volumen.
Berechnen Sie den zugehörigen Wert für . (3 P)


![Höhe [F1P1] im Schrägbild](https://assets.serlo.org/acb149e0-40f1-11ee-b109-a3f2e53ad6dd/HheF1P1imSchrgbild.svg)
