Spiegelung eines Punktes an einer Geraden

Berechnung des Spiegelpunktes $P'$ mit einer Hilfsebene $H$

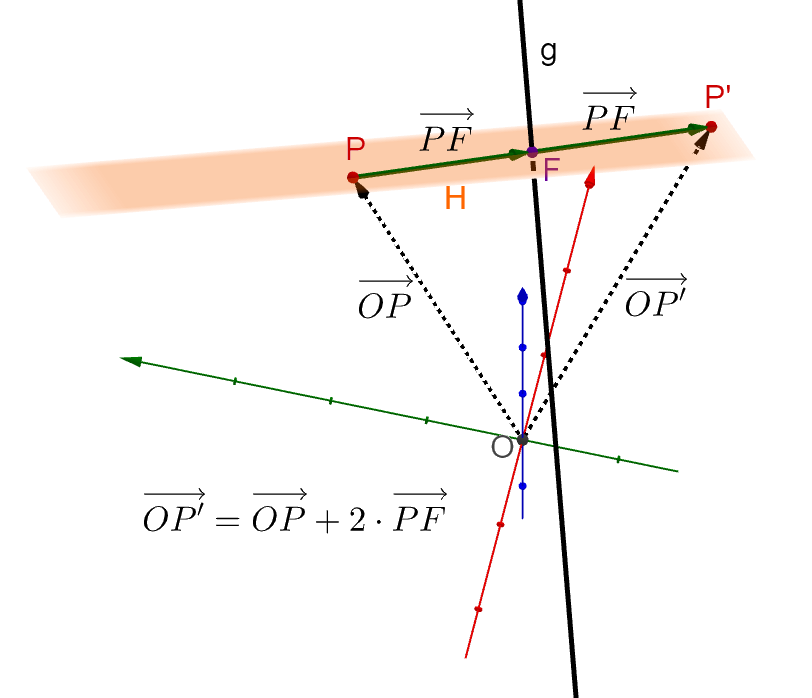
Gegeben sind ein Punkt $P$ und eine Gerade $g:\vec{x}=\overrightarrow{OA}+r\cdot\vec{u}$

Vorgehensweise

Beispiel

Gegeben sind ein Punkt $P(1|1|2)$ und eine Gerade $g: \vec x= \begin{pmatrix}3\\2\\1\end{pmatrix}+r\cdot \begin{pmatrix}2\\2\\2\end{pmatrix}$

1. Erstelle die Gleichung einer Hilfsebene $H$ mit dem gegebenen Punkt $P$ und dem Richtungsvektor der Geraden $g$ als Normalenvektor:

$H: \;\left(\vec x- \begin{pmatrix}1\\1\\2\end{pmatrix}\right)\circ \begin{pmatrix}2\\2\\2\end{pmatrix}=0$

2. Schneide $g$ mit $H$:

Setze $r=-\dfrac{1}{3}$ in die Geradengleichung ein, um den Punkt $F$ zu berechnen.

$\vec x_F= \begin{pmatrix}3\\2\\1\end{pmatrix}+(-\frac{1}{3})\cdot \begin{pmatrix}2\\2\\2\end{pmatrix}=\begin{pmatrix}3-\frac{2}{3}\\[1ex] 2-\frac{2}{3}\\[1ex]1-\frac{2}{3}\end{pmatrix}=\begin{pmatrix}\frac{7}{3}\\[1ex] \frac{4}{3}\\[1ex]\frac{1}{3}\end{pmatrix}\;\Rightarrow\;$$F(\frac{7}{3}|\frac{4}{3}|\frac{1}{3})$

3. Berechne den Vektor $\overrightarrow{PF}$

$\overrightarrow{PF}=\overrightarrow{OF}-\overrightarrow{OP}=\begin{pmatrix}\frac{7}{3}\\[1ex] \frac{4}{3}\\[1ex]\frac{1}{3}\end{pmatrix}-\begin{pmatrix}1\\1\\2\end{pmatrix}=\begin{pmatrix}\frac{4}{3}\\[1ex] \frac{1}{3}\\[1ex]-\frac{5}{3}\end{pmatrix}$

4. Setze $\overrightarrow{OP}$ und $\overrightarrow{PF}$ in die Vektorgleichung $\overrightarrow{OP'}=\overrightarrow{OP}+2\cdot\overrightarrow{PF}$ ein:

$\overrightarrow{OP'}=\begin{pmatrix}1\\1\\2\end{pmatrix}+2\cdot \begin{pmatrix}\frac{4}{3}\\[1ex] \frac{1}{3}\\[1ex]-\frac{5}{3}\end{pmatrix}=\begin{pmatrix}1+\frac{8}{3}\\[1ex]1+\frac{2}{3}\\[1ex]2-\frac{10}{3}\end{pmatrix}=\begin{pmatrix}\frac{11}{3}\\[1ex] \frac{5}{3}\\[1ex]-\frac{4}{3}\end{pmatrix}$

Antwort: Der Spiegelpunkt hat die Koordinaten $P'(\frac{11}{3}|\frac{5}{3}|-\frac{4}{3})$.

Anmerkung: Die obigen Berechnungen gelten auch im Zweidimensionalen. Die Vektoren haben dann eine Komponente weniger.