Um Geld für die beiden Aktionen einzunehmen, bietet die SMV auf dem Schulfest das Spiel "" an. Bei dem Spiel werden zwei Glücksräder mit drei bzw. vier gleich großen Sektoren verwendet, die wie in Abbildung beschriftet sind. Für einen Einsatz von darf man jedes der beiden Glücksräder einmal drehen. Für jede Ziffer , die auf den erzielten Sektoren steht, werden ausbezahlt. Die Zufallsgröße beschreibt, wie oft die Ziffer auf den erzielten Sektoren insgesamt vorkommt.
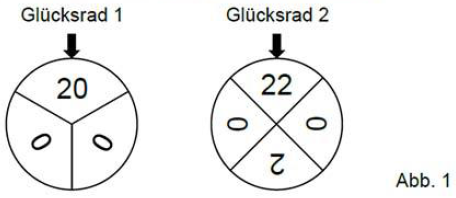
Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von . Bestimmen Sie die Wahrscheinlichkeiten und . (3 P)
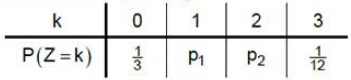
(zur Kontrolle: )
Ermitteln Sie, wie viele Spiele durchgeführt werden müssen, damit der Erwartungswert der Einnahme für die beiden Aktionen beträgt. (4 P)
Acht Personen spielen nacheinander jeweils einmal das Spiel "".
Berechnen Sie die Wahrscheinlichkeit dafür, dass die SMV mehr als zweimal mindestens ausbezahlen muss. (4 P)
%Acht Personen spielen nacheinander jeweils einmal das Spiel "".
Ermitteln Sie die Wahrscheinlichkeit dafür, dass an die ersten drei Personen drei unterschiedliche Beträge ausbezahlt werden, die in der Summe ergeben. (3 P)

