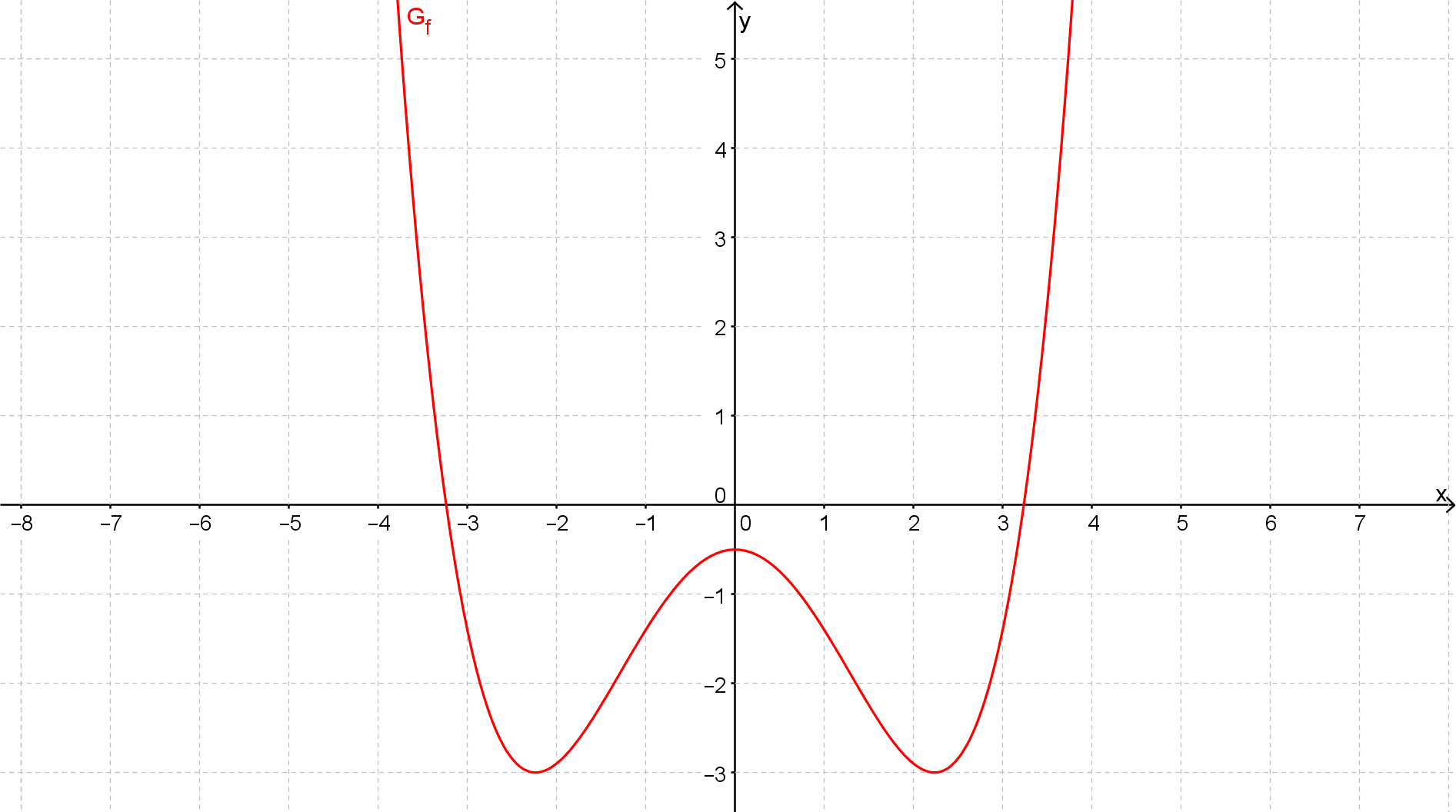
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwerte bestimmen
Gegenargument gegen Funktion
kann nicht der richtige Funktionsterm sein, da aufgrund des negativen Leitkoeffizienten -0,1 und des geraden Grades 4 für den Globalverlauf gilt:
Doch im Graph ist .
Gegenargument gegen Funktion
Der Graph von ist aufgrund der ungeraden Potenz nicht achsensymmetrisch.
Der Graph ist aber achsensymmetrisch.
Gegenargument gegen Funktion
Hier stimmt weder die Symmetrie noch der Globalverlauf!
Da einen ungeraden Grad und einen positiven Leitkoeffizienten hat, gilt für den Grenzwert bei :
Außerdem ist die Funktion aufgrund der ungeraden Exponenten nicht achsensymmetrisch.
(Sie ist auch nicht punktsymmetrisch, da sie nicht durch den Ursprung verläuft)
Begründung für Funktion
Da ausschließlich gerade Exponenten hat, ist der zugehörige Graph achsensymmetrisch.
Da der Leitkoeffizient positiv ist und der Grad gerade, hat die Funktion auch den gesuchten Globalverlauf.