Aufgaben zu absoluten und relativen Extremstellen
- 1
Wähle die richtigen Antworten aus.
Für diese Aufgabe benötigst Du folgendes Grundwissen: absolute und relative Extrema
Hier ist die Definitionsmenge nicht eingeschränkt, deshalb geht der Graph noch weiter (Ganzrationale Funktion).
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Absolute und relative Extremstellen
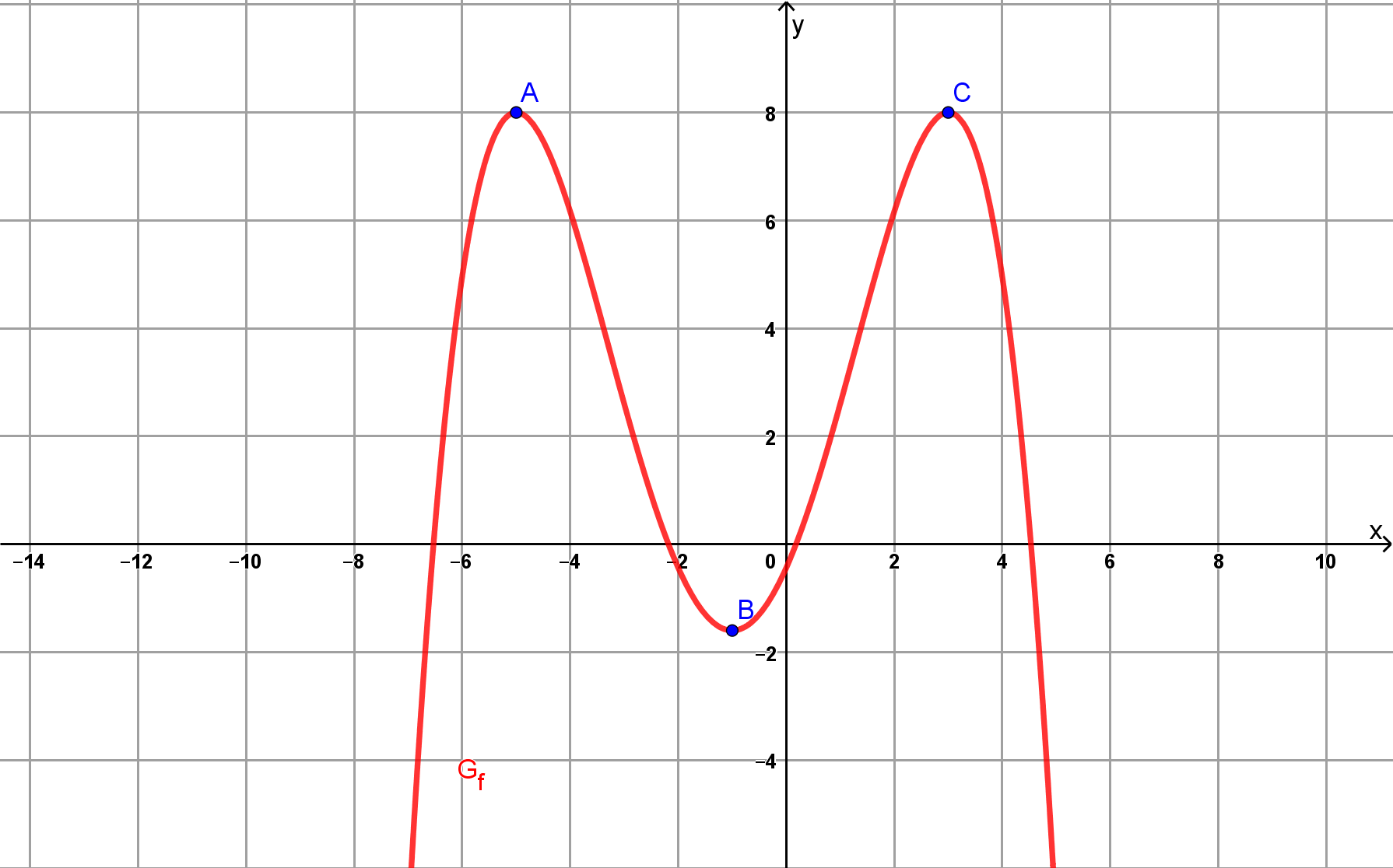
Warum sind A und C beide absolute Extrempunkte?
A und C liegen auf der exakt gleichen Höhe und haben deshalb den gleichen Funktionswert. Du siehst also, dass kein höherer Punkt mehr vorliegt und es demnach absolute Hochpunkte sind.
Warum ist B kein absoluter Extrempunkt?
B ist ein Tiefpunkt, aber man sieht, dass es noch tiefere Punkte gibt. Es kann deshalb nicht ein absoluter Extrempunkt sein. B ist darum ein relativer Extrempunkt.
Hast du eine Frage oder Feedback?
Definitionsmenge eingeschränkt oder uneingeschränkt?
- 2
Bestimme Art und Lage aller Extrempunkte. Gib die relativen und absoluten Extrempunkte an.
mit
Für diese Aufgabe benötigst Du folgendes Grundwissen: Absolute und relative Extrempunkte
1.Ableiten und Nullsetzen
Bilde die erste Ableitung der Funktion und berechne die Nullstellen.
2.Polynomdivision
Finde, zum Beispiel mithilfe einer Wertetabelle oder durch Probieren, eine Nullstelle für die Polynomdivision:
3.Mitternachtsformel
Ermittle die übrigen Nullstellen, indem du das Ergebnis der Polynomdivision nullsetzt.
Löse mit der Mitternachtsformel:
einfache Nullstelle
einfache Nullstelle
4.Vorzeichentabelle
Betrachte die Bereiche zwischen den Nullstellen der ersten Ableitung.
Der Leitkoeffizient der Funktion ist positiv und der Grad ist zusätzlich gerade.
Der Graph kommt somit von oben und geht nach oben.
Da nur einfache Nullstellen vorliegen, kommt es nach jeder Nullstelle zu einem Vorzeichenwechsel.
x
x<
-5
<x<
-1
<x<
2
<x
VZ
-
0
+
0
-
0
+
5.Berechnen der y-Werte
Setze die gefundenen x-Werte in die Funktion ein.
6.Begründung
Da der Grad der Funktion gerade ist und der Definitionsbereich nicht eingeschränkt ist, gibt es mindestens eine absolute Extremstelle. Aufgrund des positiven Leitkoeffizienten kommt der Graph von oben und geht nach oben, weshalb es sich nur um einen absoluten Tiefpunkt handeln kann.
Wenn du die y-Koordinaten der Extrempunkte miteinbeziehst, ist diese der Tiefpunkt . Die übrigen beiden Extrempunkte sind relative Extrempunkte.
Hast du eine Frage oder Feedback?
erste Ableitung bilden und Nullsetzen
Vorzeichentabelle
Berechnen der y-Werte
Begründung
1.Bilden der 1. Ableitung
Leite ab.
3x² + 3x - 6
2.Nullstellen von berechnen
und
3.Vorzeichentabelle erstellen
X
X<
-2
<X<
1
<x
VZ von f'
+
0
-
0
+
HOP
TIP
4.Berechnen der y-Werte der Extremstellen
Setze die x-Werte in die Ausgangsfunktion ein.
HOP (-2/10)
TIP (1/-3,5)
5.Betrachten des Definitonsbereichs
Aus der Angabe weißt du, dass der Definitionsbereich auf eingeschränkt ist.
6.Berechen der y-Werte der Randextremstellen
Setze die Randextrema in die Ausgangsfunktion ein.
7.Bestimmen der absoluten Extrema
Bei (-2/10) hat der Graph seinen absoluten Hochpunkt.
Bei (1/-3,5) hat der Graph seinen absoluten Tiefpunkt.
Zusatz: Angeben des Wertebereichs
]
Zur Veranschaulichung:
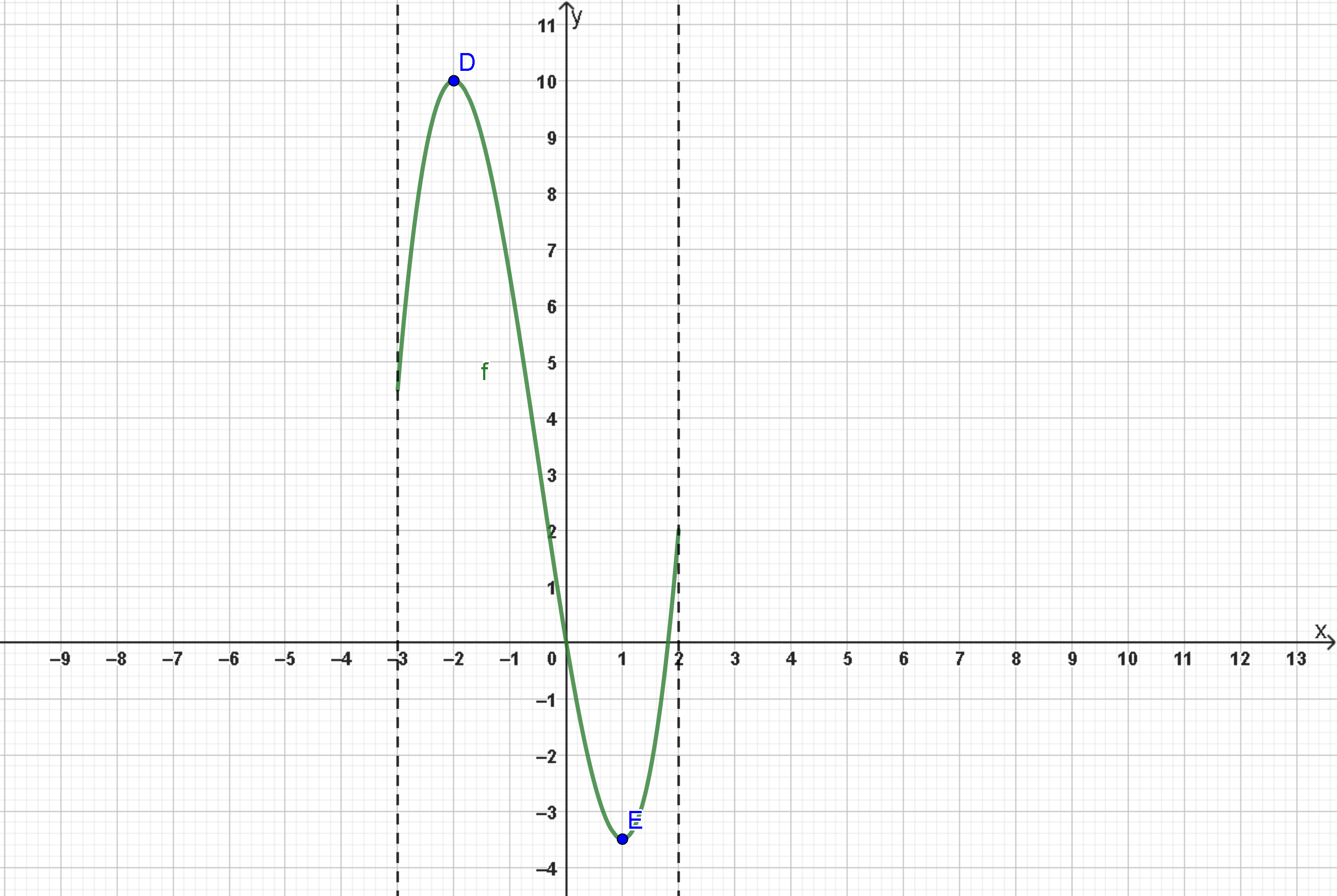
Hast du eine Frage oder Feedback?
Nullstellen von berechnen
Vorzeichentabelle erstellen
Berechnen der y-Werte der Extremstellen
Betrachten des Definitionsbereichs
Berechnen der y-Werte der Randextremstellen
Bestimmen der globalen Extrema
- 3
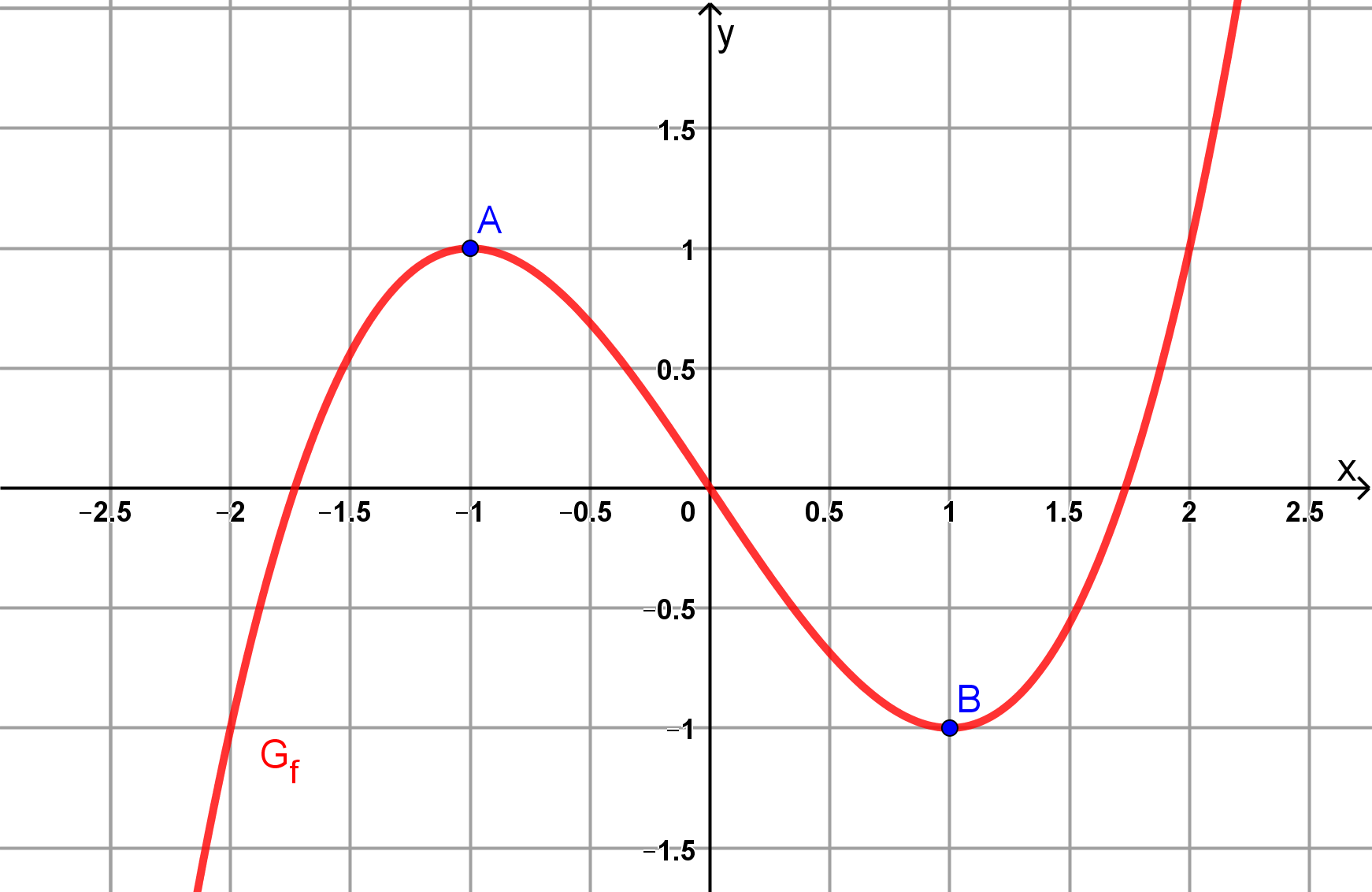
Entscheidet, ob A bzw, B ein relativer oder absoluter Extrempunkt ist.

Hier ist die Definitionsmenge nicht eingeschränkt, deshalb geht der Graph ja noch weiter.
Wäre es eine Parabel wüsste man sicher, dass kein höherer bzw, tieferer Punkt mehr folgt, sodass ein absoluter Extrempunkt garantiert wäre.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
