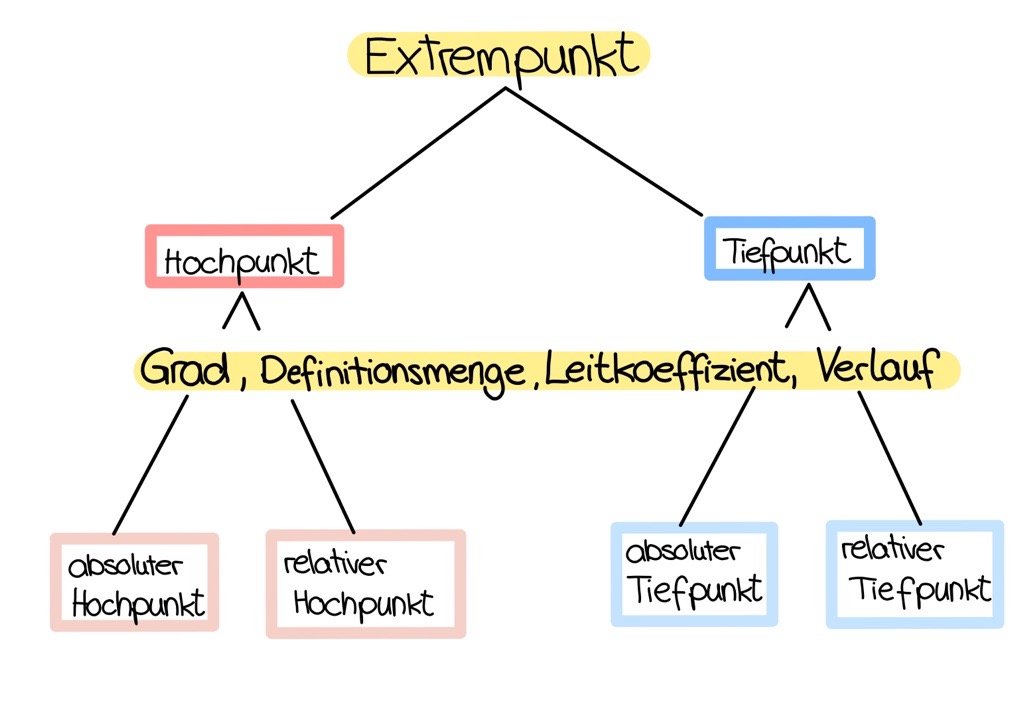
Bei Extremstellen gibt es neben der Unterscheidung zwischen Hoch- und Tiefpunkten auch die Unterscheidung von absoluten (globalen) und relativen (lokalen) Extrempunkten.
Zu beachten dabei ist die Definitionsmenge (eingeschränkt oder uneingeschränkt), der Grad, der Leitkoeffizienten und der Verlauf der Funktion.
Bilden der Ableitung
Berechnung von Art- und Lage der Extrempunkte
Definitionsmenge (eingeschränkt und uneingeschränkt)
Verhalten im Unendlichen (Verlauf des Graphen)
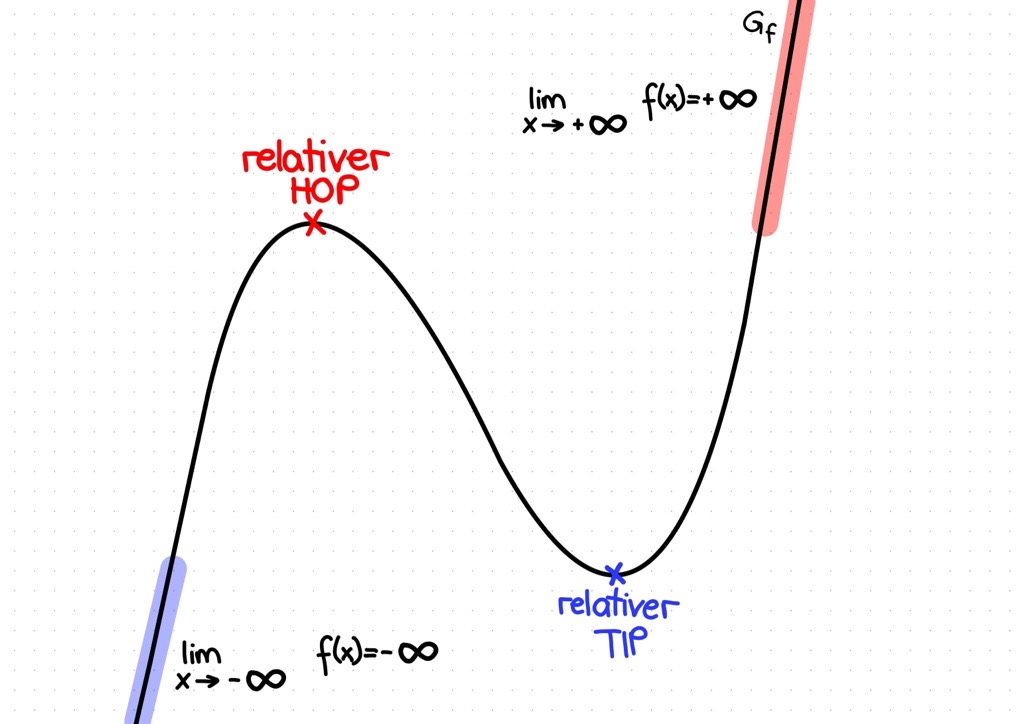
Relative Extrempunkte
Grundsätzlich sind alle Extrempunkte erstmal relativ, bevor diese genauer definiert werden.
Relative Extrempunkte sind Hochpunkte, die nicht die Höchsten und Tiefpunkte, die nicht die Tiefsten sind. Das erkennt man daran, dass die Funktion noch höhere bzw. tiefere y-Werte (Funktionswerte) hat.
Absolute Extrempunkte
Ein absoluter Extrempunkt der Funktion ist ein Punkt mit der höchsten bzw. tiefsten y-Koordinate.
Für die genauere Bestimmung der absoluten Extrempunkte muss man zusätzliches das Randextremum beachten, falls vorhanden.
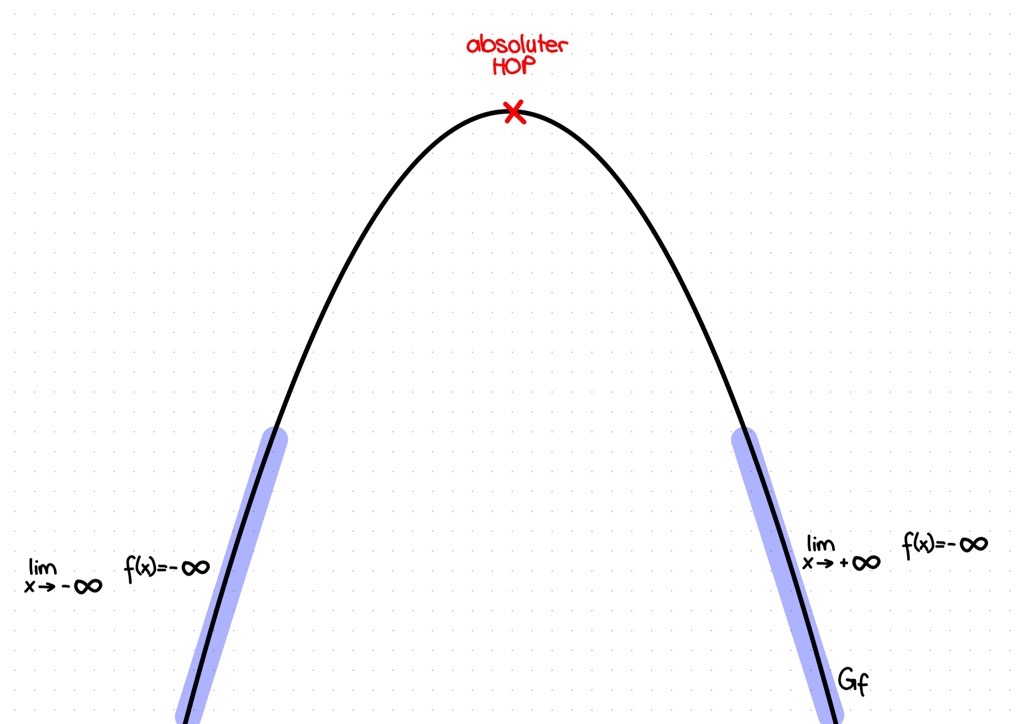
Bei Funktionen mit geradem Grad gibt es immer absolute Extrempunkte (bei eingeschränkter und uneingeschränkter Definitionsmenge).
Bei Funktionen mit ungeradem Grad und uneingeschränkter Definitionsmenge gibt es keine absoluten Extrempunkte.
Bei Funktionen mit ungeradem Grad und eingeschränkter Definitionsmenge müssen zusätzlich die Ränder der Definitionsmenge beachtet werden.
Übungsaufgaben: Absolute und relative Extremstellen
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu absoluten und relativen Extremstellen
