Eine Funktion : , deren Funktionsterm ein Polynom ist, bezeichnet man als ganzrationale Funktion oder Polynomfunktion.
Eine ganzrationale Funktion n-ten Grades ist somit eine Funktion der Form
Dabei soll nicht Null sein - sonst könnte man den Summanden ja weglassen.
Die Zahlen nennt man .
Die Zahlen bezeichnet man als .
Der größte vorkommende Exponent (hier: ) bestimmt den Grad der Polynomfunktion.
Den Koeffizienten vor dem größten vorkommenden Exponenten nennt man den Leitkoeffizienten (hier: ).
Beispiel
Die Koeffizienten sind ; und .
Die vorkommenden Exponenten sind und
hat den Grad und den Leitkoeffizienten .
Nullstellen
Eine ganzrationale Funkion -ten Grades hat höchstens Nullstellen.
Bei Polynomfunktionen bis zu Grad 2 existieren Lösungsformeln wie z.B. die Mitternachtsformel.
Bei höheren Graden hilft die Polynomdivision, ein Polynom zu vereinfachen, wenn man eine Nullstelle (z.B. durch Raten) schon kennt.
Für Polynomfunktionen 3. und 4. Grades existieren (in der Schule nicht gebräuchliche und komplizierte) Formeln. Für höhere Grade kann man keine allgemeine Formel für die Nullstellen bilden.
Grenzwerte
Lässt man gegen plus oder minus unendlich gehen, so ist der Grenzwert der Polynomfunktion immer plus oder minus unendlich. Bei ganzrationalen Funktionen geraden Grades ist das Vorzeichen der beiden Grenzwerte gleich, bei ungeradem Grad verschieden. Es entscheidet jeweils das Vorzeichen des Parameters mit der höchsten Potenz (in der Tabelle a genannt) über die Vorzeichen der Grenzwerte.
Beispiele
Im Folgenden werden die Grenzwerte der Funktionen
und
für jeweils und betrachtet.
Ungerader Grad
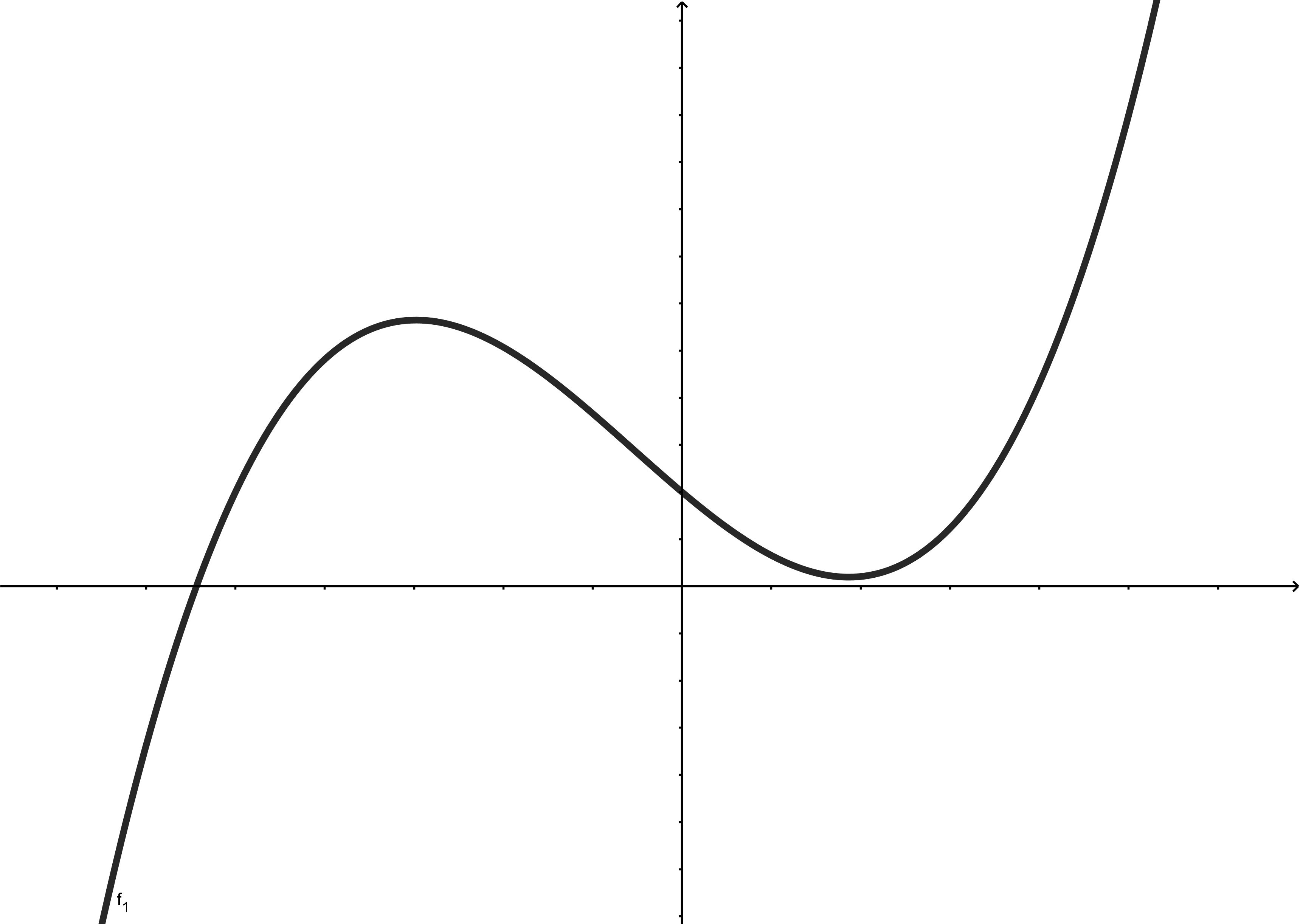 | 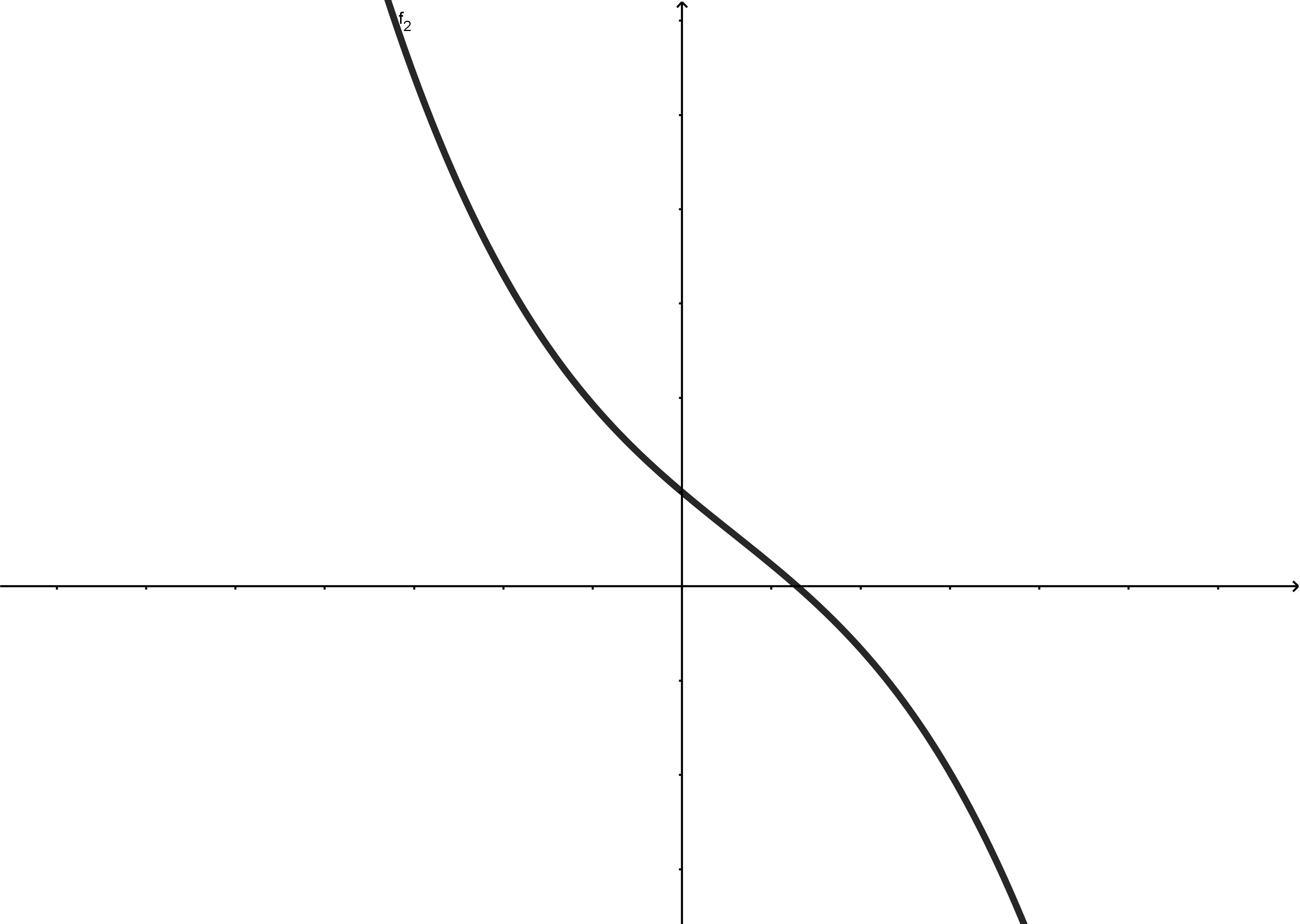 |
Gerader Grad
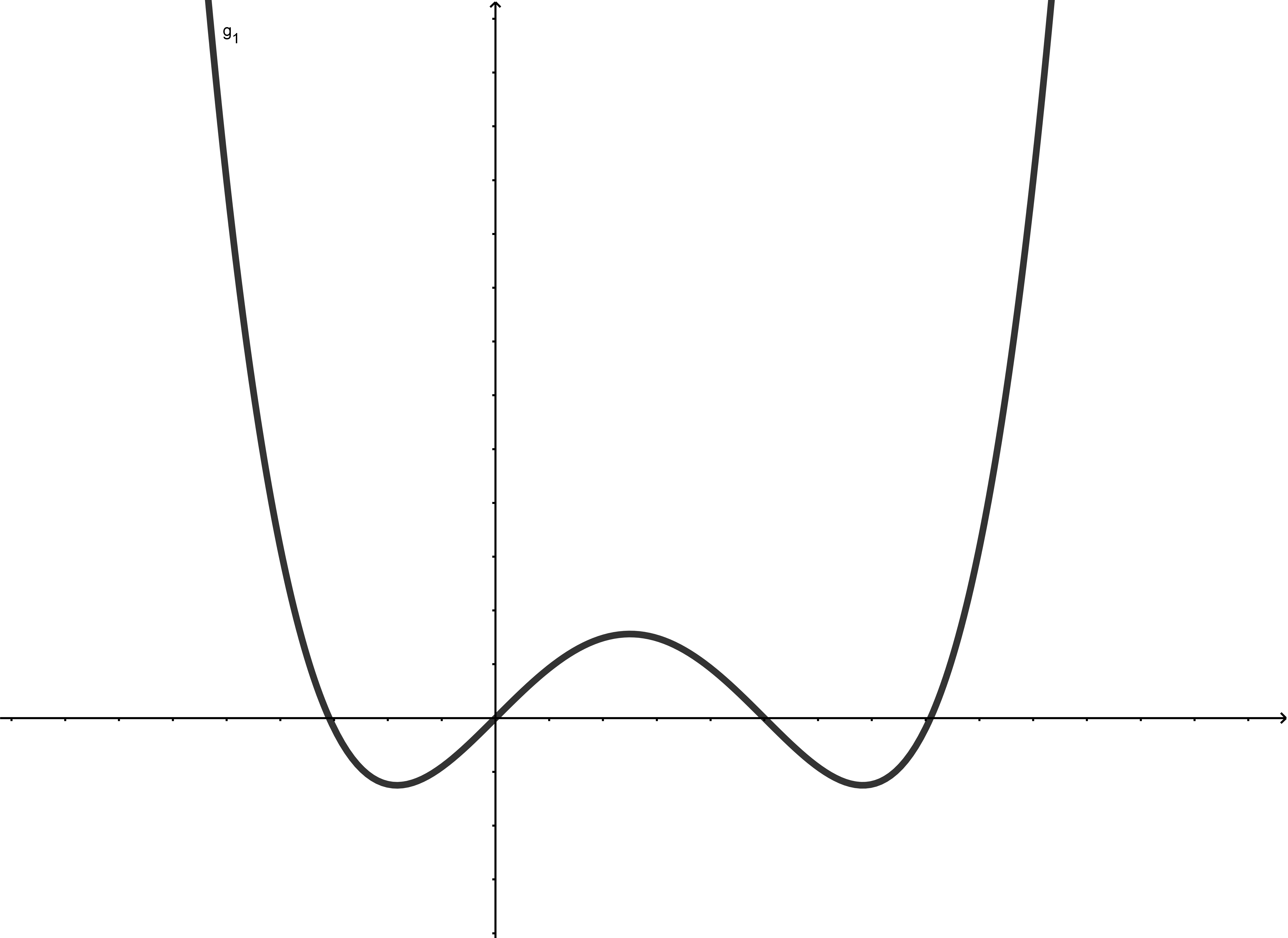 | 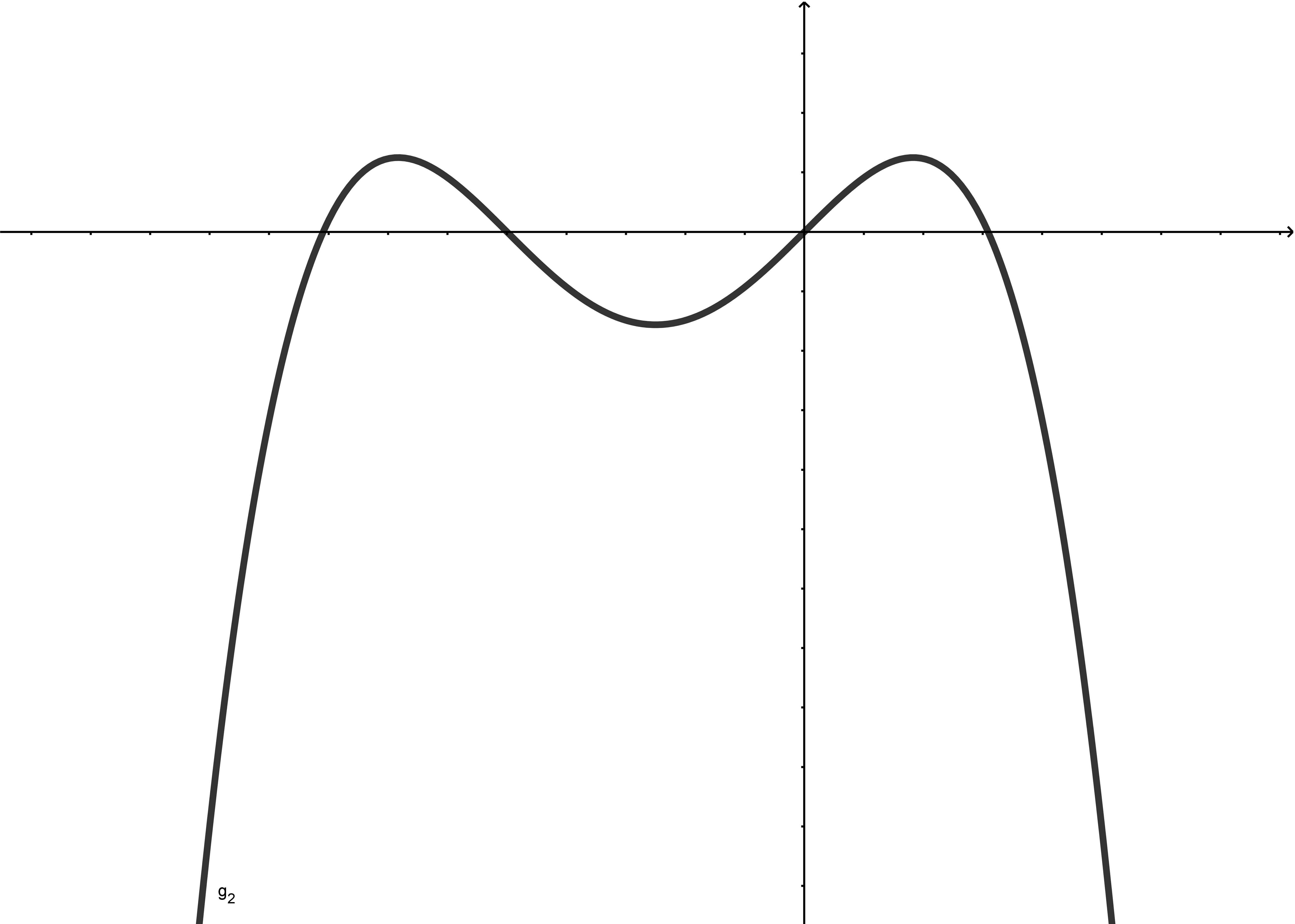 |
Spezielle Polynomfunktionen
Im Folgenden werden spezielle Polynomfunktionen vorgestellt:
Konstante Funktionen (Grad 0)
Die Konstante Funktion ordnet jedem dasselbe zu.
Der Graph der konstanten Funktion ist eine Parallele zur -Achse, die die -Achse auf der Höhe schneidet.
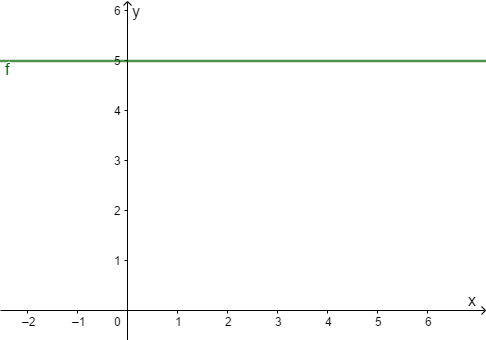
Graph der Abbildung
Lineare Funktionen (Grad 1)
Lineare Funktionen sind ganzrationale Funktionen ersten Grades. Sie haben die Form
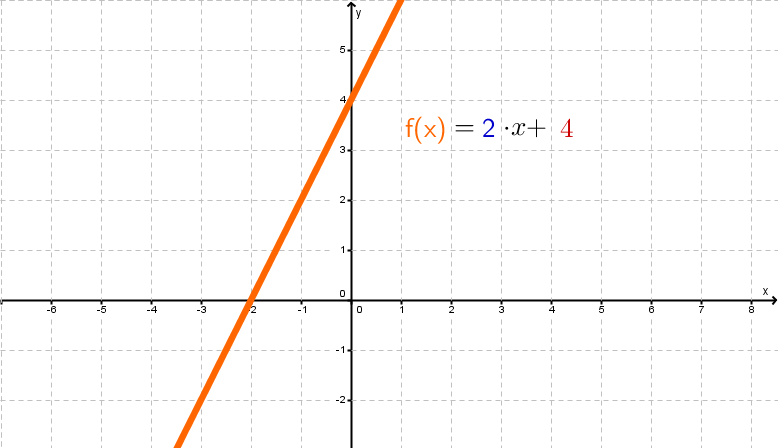
Graph der Funktion
Quadratische Funktionen (Grad 2)
Quadratische Funktionen sind Polynomfunktionen vom Grad 2. Sie haben die Form
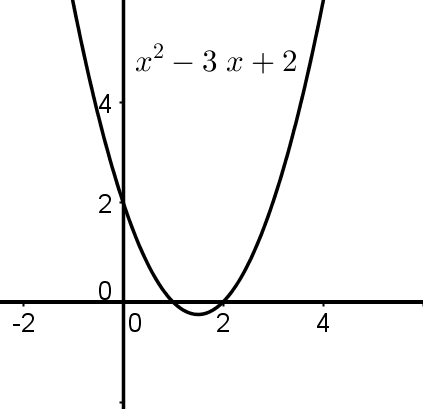
Graph der Funktion
Beispiele und Nicht-Beispiele


Extrema
Um die Extrema einer Polynomfunktion -ten Grades zu bestimmen, berechnet man zunächst die Ableitung und bestimmt davon die Nullstellen. ist eine Polynomfunktion -ten Grades. Diese hat maximal Nullstellen.
Also folgt:
Eine Polynomfunktion -ten Grades hat höchstens Extrema.
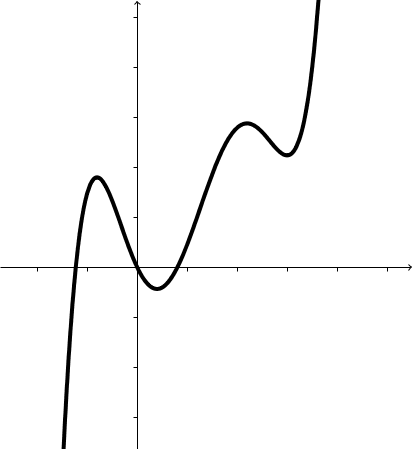
Abbildung: Graph einer Polynomfunktion 5-ten Grades
