Nachtermin Teil B - lernen mit Serlo!

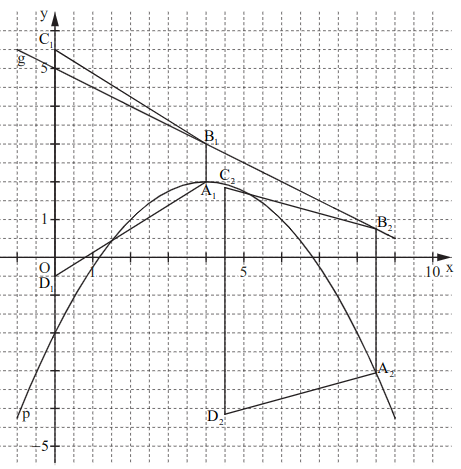
Die Parabel $p$ mit dem Scheitel $S(4\vert2)$ verläuft durch den Punkt $P(-2\vert-7)$ . Sie hat eine Gleichung der Form $y = a x^{2} + b x + c$ mit $\mathbb{G}=\mathbb{R}\times \mathbb{R}$ und $a\in\;\mathbb{R}\;\backslash\;\{0\}$ ; $b, c$ $\in\mathbb{R}$ . Die Gerade $g$ hat die Gleichung $y = - 0,5 x + 5$ mit $\mathbb{G}=\mathbb{R}\times \mathbb{R}$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Geben Sie die Gleichung der Symmetrieachse der Parabel $p$ an und zeigen Sie rechnerisch, dass die Parabel die Gleichung $y=-0{,}25x^2+2x-2$ hat.
Zeichnen Sie die Parabel $p$ und die Gerade $g$ für $x$ $\in\lbrack-1;9\rbrack$ in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit $1$ cm; $-2\leqslant x\leqslant10;\;\;-5\leqslant y\leqslant6$ .

Du weißt anschaulich, dass die Symmetrieachse einer Parabel immer durch ihren Scheitelpunkt und parallel zur $y$ -Achse verläuft. Da der Scheitelpunkt mit $S (4 ∣ 2)$ in der Aufgabenstellung angegeben ist, lautet die Gleichung der Symmetrieachse $x = 4$ .
Um zu zeigen, dass die Parabel der Gleichung $y = -0{,}25x^2+2x-2$ genügt, kannst du ausnutzen, dass die Punkte $S (4 ∣ 2)$ und $P (- 2 ∣ - 7)$ auf der Parabel $p$ liegen. Da der Scheitelpunkt bereits gegeben ist, kannst du gleich die Scheitelpunktform verwenden. Für unsere Parabel $p$ lautet sie:
$y = a \cdot (x - 4)^2 + 2.$
Um den Parameter $a$ zu bestimmen, setzt du den Punkt $P$ in die Scheitelpunktform ein und löst nach $a$ auf:
$\def\arraystretch{1.25} \begin{array}{c} -7 &=& a \cdot (-2 - 4)^2 + 2 \\ \Leftrightarrow -7 &=& a \cdot 36 + 2 \\ \Leftrightarrow -9 &=& a \cdot 36 \\ \Leftrightarrow a &=& -0{,}25 \end{array}$
Unter Ausnutzung der zweiten binomischen Formel kannst du nun die Scheitelpunktform ausmultiplizieren und erhältst die gesuchte Gleichung für $p$ :
$\def\arraystretch{1.25} \begin{array}{c} y &=& -0{,}25 \cdot (x-4)^2 + 2 \\ &=& -0{,}25 \cdot (x^2-8x+16)+2\\ &=& -0{,}25x^2 + 2x -4+2 \\ &=& -0{,}25x^2 + 2x -2 \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Punkte $A_n(x\vert-0{,}25x^2+2x-2)$ auf $p$ und Punkte $B_n(x\vert-0{,}5x+5)$ auf $g$ haben dieselbe Abszisse $x$ . Sie sind zusammen mit Punkten $C_{n}$ und $D_{n}$ Eckpunkte von gleichschenkligen Trapezen $A_{n} B_{n} C_{n} D_{n}$ mit $A_{n} B_{n} ∣ ∣ C_{n} D_{n}$ . Die Höhen $h$ der Trapeze haben eine Länge von $4\;\text{LE}$ . Weiter gilt: $\overline{C_nD_n}=6\;\text{LE}$ .
Zeichnen Sie die Trapeze $A_{1} B_{1} C_{1} D_{1}$ für $x = 4$ und $A_{2} B_{2} C_{2} D_{2}$ für $x = 8,5$ in das Koordinatensystem zu Teilaufgabe a) ein.

Siehe Abbildung in Teilaufgabe a).
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeigen Sie rechnerisch, dass für den Flächeninhalt $A$ der Trapeze $A_{n} B_{n} C_{n} D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $A_{n}$ gilt: $A(x)=(0{,}5x^2-5x+26)\;\text{FE}$ .
$[$ Teilergebnis: $\overline{A_nB_n}(x)=(0{,}25x^2-2{,}5x+7)\;\text{LE}$ $]$

Die Formel zur Berechnung des Flächeninhalts des Trapezes lautet
$\displaystyle A(x) = \frac{1}{2} \cdot \left(\overline{A_nB_n}(x)+\overline{C_nD_n}\right)\cdot h.$
Da $\overline{C_nD_n} = 6\;\text{LE}$ und $h = 4 \;\text{LE}$ bereits gegeben sind, musst du noch die Länge der Strecke $\overline{A_nB_n}(x)$ berechnen. Da die Punkte $A_{n}$ und $B_{n}$ die gleiche Abszisse $x$ haben, berechnet sich die Länge $\overline{A_nB_n}(x)$ aus der Differenz der $y$ -Koordinaten von $A_{n}$ und $B_{n}$ :
$\def\arraystretch{1.25} \begin{array}{c} \overline{A_nB_n}(x) = y_{B_n}(x) - y_{A_n}(x) &=& -0{,}5x + 5 - (-0{,}25x^2+2x-2)\ \text{LE}\\ &=& (0{,}25x^2 - 2{,}5x +7) \ \text{LE}. \end{array}$
Der Flächeninhalt des Trapezes ist dann:
$\displaystyle \def\arraystretch{2} \begin{array}{c} A(x) &=& \dfrac{1}{2}\cdot \left(\overline{A_nB_n}(x) + \overline{C_nD_n} \right)\cdot h \\ &=& \dfrac{1}{2}\cdot \left(0{,}25x^2-2{,}5x + 7 + 6 \right)\ \text{LE}\cdot 4 \ \text{LE} \\ &=& \left(0{,}5x^2-5x+26\right) \ \text{FE}. \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Unter den Trapezen $A_{n} B_{n} C_{n} D_{n}$ hat das Trapez $A_{0} B_{0} C_{0} D_{0}$ den minimalen Flächeninhalt.
Berechnen Sie den Flächeninhalt des Trapezes $A_{0} B_{0} C_{0} D_{0}$ und den zugehörigen Wert für $x$ .

Du hast in Aufgabe c) eine allgemeine Formel $A (x)$ zur Berechnung des Flächeninhalts des Trapezes berechnet. Man erkennt, dass $A (x)$ eine nach oben offene Parabel beschreibt, denn $A (x)$ ist eine Gleichung von der Form $a x^{2} + b x + c$ mit $a > 0$ . Um nun den minimalen Flächeninhalt zu berechnen, musst du die Formel für $A (x)$ mithilfe einer quadratischen Ergänzung in die Scheitelpunktform überführen, denn daraus kannst du den Scheitelpunkt und damit den minimalen Wert des Flächeninhalts direkt ablesen:
$\def\arraystretch{1.25} \begin{array}{c} A(x) &=& 0{,}5x^2-5x+26 \\ &=& 0{,}5 \cdot \left(x^2-10x \right) + 26 \\ &=& 0{,}5 \cdot \left(x^2-2\cdot 5x + 5^2 - 5^2\right) + 26\\ &=& 0{,}5 \cdot \left[\left(x-5\right)^2 - 25\right] + 26 \\ &=& 0{,}5 \cdot \left(x-5\right)^2 - 12{,}5 + 26 \\ &=& 0{,}5 \cdot \left(x-5\right)^2 + 13{,}5. \end{array}$
An dieser Darstellung erkennen wir, dass die Koordinaten des Scheitelpunktes von $A (x)$ $x = 5$ und $y = 13,5$ lauten. Somit ist $A_{\text{min}} = 13{,}5 \ \text{FE}$ für $x = 5.$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Trapeze $A_{3} B_{3} C_{3} D_{3}$ und $A_{4} B_{4} C_{4} D_{4}$ haben einen Flächeninhalt von $25\;\text{FE}$ . Berechnen Sie die zugehörigen Werte für $x$ .
Sind diese Trapeze Rechtecke? Begründen Sie Ihre Entscheidung.
- Diese Trapeze sind Rechtecke.
- Diese Trapeze sind keine Rechtecke.
Mithilfe der Formel aus Aufgabe c) setzt man:
$\displaystyle \def\arraystretch{1.25} \begin{array}{c} 25 &=& 0{,}5x^2 - 5x + 26 \\ \Leftrightarrow 0 &=& 0{,}5x^2-5x + 1 \end{array}$
und löst mit der Mitternachtsformel:
$\displaystyle \def\arraystretch{2} \begin{array}{c} x_{1{,}2} &=& \dfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 0{,}5 \cdot 1}}{2 \cdot 0{,}5} \\ &=& 5 \pm \sqrt{23}. \end{array}$
Damit ist $x_1 = 5 + \sqrt{23} \approx 9{,}80$ und $x_2 = 5 - \sqrt{23} \approx 0{,}20$ .
In einem Rechteck sind gegenüberliegende Seiten gleich lang. Du weißt, dass in jedem Fall $\overline{C_nD_n}=6\;\text{LE}$ gelten soll. Also muss
$\overline{A_3B_3}= \overline{A_4B_4}=\overline{C_3D_3}= \overline{C_4D_4}=6 \ \text{LE}.$
Da in einem Rechteck auch alle vorkommenden Winkel rechtwinklig ( $90 °$ ) sind, muss
$\displaystyle \overline{A_3D_3}= \overline{B_3C_3}= \overline{B_4C_4}= \overline{A_4D_4}= h = 4 \ \text{LE}$
gelten. In diesem Fall würde sich aber ein Flächeninhalt von
$A = 6 \ \text{LE} \cdot 4 \ \text{LE} = 24 \ \text{FE}$
ergeben. Damit können die Trapeze keine Rechtecke sein.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechnen Sie das Maß $\varepsilon$ des Winkels $D_{1} C_{1} B_{1}$ .

Bei dieser Teilaufgabe gibt es mehrere Lösungswege. Der vermutlich einfachste verwendet den Tangens, denn es gilt (wie zum Beispiel anhand der Skizze aus Teilaufgabe b) erkannt werden kann):
$\def\arraystretch{2} \begin{array}{c} \tan \varepsilon = \dfrac{\text{Gegenkathete}}{\text{{Ankathete}}} &=& \dfrac{h}{0{,}5 \cdot \left(\overline{C_1D_1}-\overline{A_1B_1}\right)} \\ &=& \dfrac{4}{0{,}5 \cdot \left(6- (0{,}25\cdot 4^2 - 2{,}5\cdot 4 +7)\right)} \\ &=&\dfrac{4}{0{,}5 \cdot (6-1)} \\ &=& 1{,}6 \end{array}$
Wendest du nun die Umkehrfunktion des Tangens an, so erhältst du für den Winkel $\varepsilon$ :
$\varepsilon = \tan^{-1}(1{,}6) \approx 57{,}99°.$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?