Nachtermin Teil B

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Parabel $p$ mit dem Scheitel $S(4\vert2)$ verläuft durch den Punkt $P(-2\vert-7)$ . Sie hat eine Gleichung der Form $y = a x^{2} + b x + c$ mit $\mathbb{G}=\mathbb{R}\times \mathbb{R}$ und $a\in\;\mathbb{R}\;\backslash\;\{0\}$ ; $b, c$ $\in\mathbb{R}$ . Die Gerade $g$ hat die Gleichung $y = - 0,5 x + 5$ mit $\mathbb{G}=\mathbb{R}\times \mathbb{R}$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1. Geben Sie die Gleichung der Symmetrieachse der Parabel $p$ an und zeigen Sie rechnerisch, dass die Parabel die Gleichung $y=-0{,}25x^2+2x-2$ hat.
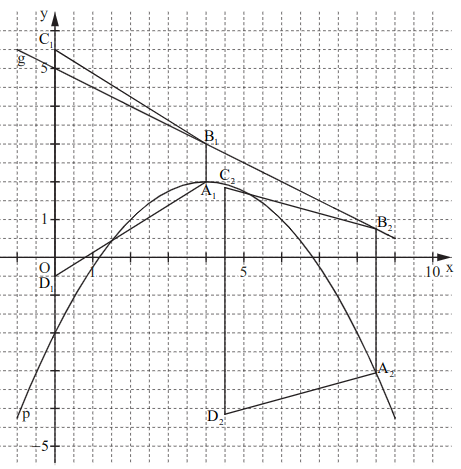
  Zeichnen Sie die Parabel $p$ und die Gerade $g$ für $x$ $\in\lbrack-1;9\rbrack$ in ein Koordinatensystem.
  Für die Zeichnung: Längeneinheit $1$ cm; $-2\leqslant x\leqslant10;\;\;-5\leqslant y\leqslant6$ .
  
  Du weißt anschaulich, dass die Symmetrieachse einer Parabel immer durch ihren Scheitelpunkt und parallel zur $y$ -Achse verläuft. Da der Scheitelpunkt mit $S (4 ∣ 2)$ in der Aufgabenstellung angegeben ist, lautet die Gleichung der Symmetrieachse $x = 4$ .
  Um zu zeigen, dass die Parabel der Gleichung $y = -0{,}25x^2+2x-2$ genügt, kannst du ausnutzen, dass die Punkte $S (4 ∣ 2)$ und $P (- 2 ∣ - 7)$ auf der Parabel $p$ liegen. Da der Scheitelpunkt bereits gegeben ist, kannst du gleich die Scheitelpunktform verwenden. Für unsere Parabel $p$ lautet sie:
  $y = a \cdot (x - 4)^2 + 2.$
  Um den Parameter $a$ zu bestimmen, setzt du den Punkt $P$ in die Scheitelpunktform ein und löst nach $a$ auf:
  $\def\arraystretch{1.25} \begin{array}{c} -7 &=& a \cdot (-2 - 4)^2 + 2 \\ \Leftrightarrow -7 &=& a \cdot 36 + 2 \\ \Leftrightarrow -9 &=& a \cdot 36 \\ \Leftrightarrow a &=& -0{,}25 \end{array}$
  Unter Ausnutzung der zweiten binomischen Formel kannst du nun die Scheitelpunktform ausmultiplizieren und erhältst die gesuchte Gleichung für $p$ :
  $\def\arraystretch{1.25} \begin{array}{c} y &=& -0{,}25 \cdot (x-4)^2 + 2 \\ &=& -0{,}25 \cdot (x^2-8x+16)+2\\ &=& -0{,}25x^2 + 2x -4+2 \\ &=& -0{,}25x^2 + 2x -2 \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Punkte $A_n(x\vert-0{,}25x^2+2x-2)$ auf $p$ und Punkte $B_n(x\vert-0{,}5x+5)$ auf $g$ haben dieselbe Abszisse $x$ . Sie sind zusammen mit Punkten $C_{n}$ und $D_{n}$ Eckpunkte von gleichschenkligen Trapezen $A_{n} B_{n} C_{n} D_{n}$ mit $A_{n} B_{n} ∣ ∣ C_{n} D_{n}$ . Die Höhen $h$ der Trapeze haben eine Länge von $4\;\text{LE}$ . Weiter gilt: $\overline{C_nD_n}=6\;\text{LE}$ .
  Zeichnen Sie die Trapeze $A_{1} B_{1} C_{1} D_{1}$ für $x = 4$ und $A_{2} B_{2} C_{2} D_{2}$ für $x = 8,5$ in das Koordinatensystem zu Teilaufgabe a) ein.
  
  Siehe Abbildung in Teilaufgabe a).
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Zeigen Sie rechnerisch, dass für den Flächeninhalt $A$ der Trapeze $A_{n} B_{n} C_{n} D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $A_{n}$ gilt: $A(x)=(0{,}5x^2-5x+26)\;\text{FE}$ .
  $[$ Teilergebnis: $\overline{A_nB_n}(x)=(0{,}25x^2-2{,}5x+7)\;\text{LE}$ $]$
  
  Die Formel zur Berechnung des Flächeninhalts des Trapezes lautet
  $\displaystyle A(x) = \frac{1}{2} \cdot \left(\overline{A_nB_n}(x)+\overline{C_nD_n}\right)\cdot h.$
  Da $\overline{C_nD_n} = 6\;\text{LE}$ und $h = 4 \;\text{LE}$ bereits gegeben sind, musst du noch die Länge der Strecke $\overline{A_nB_n}(x)$ berechnen. Da die Punkte $A_{n}$ und $B_{n}$ die gleiche Abszisse $x$ haben, berechnet sich die Länge $\overline{A_nB_n}(x)$ aus der Differenz der $y$ -Koordinaten von $A_{n}$ und $B_{n}$ :
  $\def\arraystretch{1.25} \begin{array}{c} \overline{A_nB_n}(x) = y_{B_n}(x) - y_{A_n}(x) &=& -0{,}5x + 5 - (-0{,}25x^2+2x-2)\ \text{LE}\\ &=& (0{,}25x^2 - 2{,}5x +7) \ \text{LE}. \end{array}$
  Der Flächeninhalt des Trapezes ist dann:
  $\displaystyle \def\arraystretch{2} \begin{array}{c} A(x) &=& \dfrac{1}{2}\cdot \left(\overline{A_nB_n}(x) + \overline{C_nD_n} \right)\cdot h \\ &=& \dfrac{1}{2}\cdot \left(0{,}25x^2-2{,}5x + 7 + 6 \right)\ \text{LE}\cdot 4 \ \text{LE} \\ &=& \left(0{,}5x^2-5x+26\right) \ \text{FE}. \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Unter den Trapezen $A_{n} B_{n} C_{n} D_{n}$ hat das Trapez $A_{0} B_{0} C_{0} D_{0}$ den minimalen Flächeninhalt.
  Berechnen Sie den Flächeninhalt des Trapezes $A_{0} B_{0} C_{0} D_{0}$ und den zugehörigen Wert für $x$ .
  
  Du hast in Aufgabe c) eine allgemeine Formel $A (x)$ zur Berechnung des Flächeninhalts des Trapezes berechnet. Man erkennt, dass $A (x)$ eine nach oben offene Parabel beschreibt, denn $A (x)$ ist eine Gleichung von der Form $a x^{2} + b x + c$ mit $a > 0$ . Um nun den minimalen Flächeninhalt zu berechnen, musst du die Formel für $A (x)$ mithilfe einer quadratischen Ergänzung in die Scheitelpunktform überführen, denn daraus kannst du den Scheitelpunkt und damit den minimalen Wert des Flächeninhalts direkt ablesen:
  $\def\arraystretch{1.25} \begin{array}{c} A(x) &=& 0{,}5x^2-5x+26 \\ &=& 0{,}5 \cdot \left(x^2-10x \right) + 26 \\ &=& 0{,}5 \cdot \left(x^2-2\cdot 5x + 5^2 - 5^2\right) + 26\\ &=& 0{,}5 \cdot \left[\left(x-5\right)^2 - 25\right] + 26 \\ &=& 0{,}5 \cdot \left(x-5\right)^2 - 12{,}5 + 26 \\ &=& 0{,}5 \cdot \left(x-5\right)^2 + 13{,}5. \end{array}$
  An dieser Darstellung erkennen wir, dass die Koordinaten des Scheitelpunktes von $A (x)$ $x = 5$ und $y = 13,5$ lauten. Somit ist $A_{\text{min}} = 13{,}5 \ \text{FE}$ für $x = 5.$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Die Trapeze $A_{3} B_{3} C_{3} D_{3}$ und $A_{4} B_{4} C_{4} D_{4}$ haben einen Flächeninhalt von $25\;\text{FE}$ . Berechnen Sie die zugehörigen Werte für $x$ .
  Sind diese Trapeze Rechtecke? Begründen Sie Ihre Entscheidung.
  Diese Trapeze sind Rechtecke.
  Diese Trapeze sind keine Rechtecke.
  
  Mithilfe der Formel aus Aufgabe c) setzt man:
  $\displaystyle \def\arraystretch{1.25} \begin{array}{c} 25 &=& 0{,}5x^2 - 5x + 26 \\ \Leftrightarrow 0 &=& 0{,}5x^2-5x + 1 \end{array}$
  und löst mit der Mitternachtsformel:
  $\displaystyle \def\arraystretch{2} \begin{array}{c} x_{1{,}2} &=& \dfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 0{,}5 \cdot 1}}{2 \cdot 0{,}5} \\ &=& 5 \pm \sqrt{23}. \end{array}$
  Damit ist $x_1 = 5 + \sqrt{23} \approx 9{,}80$ und $x_2 = 5 - \sqrt{23} \approx 0{,}20$ .
  In einem Rechteck sind gegenüberliegende Seiten gleich lang. Du weißt, dass in jedem Fall $\overline{C_nD_n}=6\;\text{LE}$ gelten soll. Also muss
  $\overline{A_3B_3}= \overline{A_4B_4}=\overline{C_3D_3}= \overline{C_4D_4}=6 \ \text{LE}.$
  Da in einem Rechteck auch alle vorkommenden Winkel rechtwinklig ( $90 °$ ) sind, muss
  $\displaystyle \overline{A_3D_3}= \overline{B_3C_3}= \overline{B_4C_4}= \overline{A_4D_4}= h = 4 \ \text{LE}$
  gelten. In diesem Fall würde sich aber ein Flächeninhalt von
  $A = 6 \ \text{LE} \cdot 4 \ \text{LE} = 24 \ \text{FE}$
  ergeben. Damit können die Trapeze keine Rechtecke sein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. Berechnen Sie das Maß $\varepsilon$ des Winkels $D_{1} C_{1} B_{1}$ .
  
  Bei dieser Teilaufgabe gibt es mehrere Lösungswege. Der vermutlich einfachste verwendet den Tangens, denn es gilt (wie zum Beispiel anhand der Skizze aus Teilaufgabe b) erkannt werden kann):
  $\def\arraystretch{2} \begin{array}{c} \tan \varepsilon = \dfrac{\text{Gegenkathete}}{\text{{Ankathete}}} &=& \dfrac{h}{0{,}5 \cdot \left(\overline{C_1D_1}-\overline{A_1B_1}\right)} \\ &=& \dfrac{4}{0{,}5 \cdot \left(6- (0{,}25\cdot 4^2 - 2{,}5\cdot 4 +7)\right)} \\ &=&\dfrac{4}{0{,}5 \cdot (6-1)} \\ &=& 1{,}6 \end{array}$
  Wendest du nun die Umkehrfunktion des Tangens an, so erhältst du für den Winkel $\varepsilon$ :
  $\varepsilon = \tan^{-1}(1{,}6) \approx 57{,}99°.$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
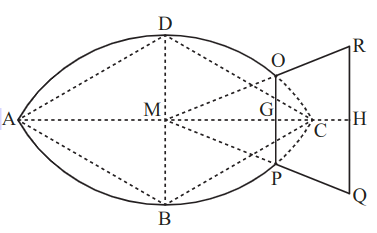
Unten ist die Vorlage für ein Firmenlogo in Form eines Fisches skizziert. Die Raute $A B C D$ mit dem Diagonalenschnittpunkt $M$ ist Grundlage für den Fischkörper, der durch den Kreisbogen $\overset\frown{OA}$ um den Mittelpunkt $B$ , den Kreisbogen $\overset\frown{AP}$ um den Mittelpunkt $D$ und die Strecke $[O P]$ begrenzt wird. Das gleichschenklige Trapez $O P Q R$ bildet die Schwanzflosse.
Es gilt: $\overline{BM}=3$ cm; $\overline{BC}=6$ cm; $\overline{MH}=6{,}5$ cm; $\overline{RQ}=5{,}2$ cm; $DB\parallel OP\parallel RQ$ . Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1. Berechnen Sie die Länge der Strecke $[C M]$ und zeigen Sie, dass für das Maß $\beta$ des Winkels $C B A$ gilt: $\beta=120^\circ$ .
  $[$ Ergebnis: $\overline{CM}=5{,}20$ cm $]$
  
  Zur Berechnung der Streckenlänge $\overline{CM}$ kannst du den Satz des Pythagoras im rechtwinkligen Dreieck $C M B$ verwenden. In diesem Dreieck ist $[B C]$ die Hypotenuse der Länge $\overline{BC} = 6\;\text{cm}$ , da der rechte Winkel beim Punkt $M$ liegt. Beachtest du, dass $\overline{BM} = 3\;\text{cm}$ gegeben ist und bezeichnen $\overline{CM} = x$ , so gilt allgemein:
  $x^2 + \overline{BM}^2 = \overline{BC}^2.$
  Setzt du nun die konkreten Zahlenwerte ein und löst die Gleichung nach $x$ auf, so erhältst du:
  $\displaystyle \def\arraystretch{1.25} \begin{array}{cc} && x^2 + 3^2 &=& 6^2 \\ \Leftrightarrow&& x^2 &=& 6^2 - 3^2 &=& 36 - 9 = 27 \end{array}$
  Ziehst du nun aus $x^{2} = 27$ die Wurzel, so erhältst du $x = 3 \sqrt{3} \approx 5{,}20\;\text{cm}$ . Dabei solltest du die Lösung mit dem negativen Vorzeichen vernachlässigen, da eine negative Streckenlänge im Anwendungskontext sinnlos ist.
  Um den angegebenen Winkel zu berechnen, gibt es zwei Möglichkeiten:
  Variante 1: Verwendung der Eigenschaften eines gleichschenkligen Dreiecks
  Der Abbildung kannst du entnehmen, dass die Dreiecke $A B D$ und $B C D$ gleichschenklig sind. Du weißt, dass in gleichschenkligen Dreiecken die beiden Basiswinkel immer den Wert $60 °$ annehmen. Also kannst du berechnen:
  $\displaystyle \beta = 2 \cdot 60° = 120°.$
  Variante 2: Verwende den Kosinus
  Falls du die Argumentation mithilfe der gleichschenkligen Dreiecke in Variante 1 nicht direkt gesehen hast, kannst du den gesuchten Winkel natürlich auch berechnen. Dazu betrachten wir das Dreieck $M B C$ . Den Winkel $\sphericalangle CBM$ in diesem Dreieck kannst du zum Beispiel über den Kosinus berechnen:
  $\cos(\sphericalangle CBM) = \dfrac{\text{Ankathete}}{\text{{Hypotenuse}}} = \dfrac{\overline{MB}}{\overline{BC}} = \dfrac{3 \ \text{cm}}{6 \ \text{cm}} = \dfrac{1}{2}.$
  Wendest du nun die Umkehrfunktion des Kosinus an, so erhältst du für den Winkel $\sphericalangle CBM$ :
  $\cos^{-1}\left(\dfrac{1}{2}\right) = 60°$
  Insgesamt gilt nun $\beta = \sphericalangle CBA = 2 \cdot \sphericalangle CBM = 2 \cdot 60° = 120°.$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Zeichnen Sie die Vorlage des Firmenlogos.
  
  Firmenlogo
  In Aufgabe a) wurde $\overline {CM}=5{,}2\;\text{cm}$ berechnet. Die Zeichnung erfolgt mithilfe dieses Ergebnisses.
  Zeichne einen Strahl, beginnend in einem Punkt $A$ . Trage auf dem Strahl die Strecke
  $\overline {AM}=\overline {CM}=5{,}2\;\text{cm}$ beginnend im Punkt $A$ ab.
  Trage auf dem Strahl, erneut die Strecke $\overline {AM}=\overline {CM}=5{,}2\;\text{cm}$ beginnend im Punkt $M$ ab. Du erhältst den Punkt $C$ .
  Errichte im Punkt $M$ eine Mittelsenkrechte und zeichne um $M$ einen Kreis mit dem Radius $r=\overline {BM}=3\;\text{cm}.$
  Der Kreis schneidet die Mittelsenkrechte in den Punkten $B$ und $D$ .
  Verbinde $A$ mit $D$ , $D$ mit $C$ , $C$ mit $B$ und $B$ mit $A$ .
  Trage auf dem Strahl die Strecke
  $\overline {MH}=6{,}5\;\text{cm}$ beginnend im Punkt $M$ ab.
  Du erhältst den Punkt $H$ .
  Errichte im Punkt $H$ eine Mittelsenkrechte und zeichne um $H$ einen Kreis mit dem Radius $r=\dfrac{1}{2}\overline {RQ}=2{,}6\;\text{cm}$ . Der Kreis schneidet die Mittelsenkrechte in den Punkten $R$ und $Q$ .
  Anmerkung: Zur besseren Übersichtlichkeit wurden Hilfslinien entfernt.
  Verbinde $M$ mit $R$ und $M$ mit $Q$ .
  Zeichne den Kreisbogen $\overset\frown{OA}$ um den Mittelpunkt $B$ . Der Kreisbogen $\overset\frown{OA}$ schneidet die Strecke $[M R]$ im Punkt $O$ . Zeichne den Kreisbogen $\overset\frown{AP}$ um den Mittelpunkt $D$ . Der Kreisbogen $\overset\frown{OA}$ schneidet die Strecke $[M Q]$ im Punkt $P$ .
  Verbinde $O$ mit $P$ .
  Das fertige Firmenlogo sieht dann so aus.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Für die Strecke $[O P]$ gilt: $\overline{OP}=0{,}6\cdot\overline{RQ}$ . Berechnen Sie die Längen der Strecken $[M G]$ und $[O R]$ .
  $[$ Ergebnisse: $\overline{MG}=3{,}90\;\text{cm}$ ; $\overline{OR}=2{,}80\;\text{cm}$ $]$
  
  Um die Streckenlänge $\overline{MG}$ zu berechnen, musst du bei dieser Teilaufgabe den Strahlensatz verwenden. Es gilt die Verhältnisgleichung:
  $\displaystyle \dfrac{\overline{MG}}{\overline{MH}} = \dfrac{\overline{OP}}{\overline{RQ}} = \dfrac{0{,}6 \cdot \overline{RQ}}{\overline{RQ}} = 0{,}6.$
  Wenn du diese Gleichung nun nach der gesuchten Streckenlänge $\overline{MG}$ umstellst, so erhältst du:
  $\overline{MG} = 0{,}6 \cdot \overline{MH} = 0{,}6 \cdot 6{,}5 \ \text{cm} = 3{,}9 \ \text{cm}.$
  Die Berechnung der zweiten Streckenlänge $\overline{OR}$ ist etwas komplizierter, denn neben dem Strahlensatz musst du hier auch den Satz des Pythagoras verwenden.
  Mit dem Satz des Pythagoras kannst du zunächst die Streckenlänge $\overline{MR}$ berechnen. Im Dreieck $M H R$ gilt nämlich:
  $\displaystyle \overline{MR}^2 = \overline{MH}^2 + \left( \dfrac{1}{2}\cdot \overline{RQ} \right)^2.$
  Da $\overline{MH} = 6{,}5\;\text{cm}$ und $\overline{RQ} = 5{,}2 \;\text{cm}$ gegeben sind, kannst du dies direkt einsetzen und erhältst:
  $\displaystyle \overline{MR}^2 = (6{,}5 \ \text{cm})^2 + \left( \dfrac{1}{2} \cdot 5{,}2 \ \text{cm} \right)^2 = 49{,}01 \ \text{cm}^2.$
  Ziehst du nun die Wurzel und vernachlässigst wie oben die Lösung mit dem negativen Vorzeichen, so gilt:
  $\displaystyle \overline{MR} = 7{,}00 \ \text{cm}.$
  Nun sollte man feststellen, dass nach dem Strahlensatz die Verhältnisgleichung
  $\displaystyle \dfrac{\overline{MO}}{\overline{MR}} = \dfrac{\overline{MG}}{\overline{MH}} = \dfrac{3{,}9 \ \text{cm}}{6{,}5 \ \text{cm}} = 0{,}6$
  gilt. Diese kannst du direkt nach der einzigen noch unbekannten Größe $\overline{MO}$ auflösen und gleichzeitig dein oben berechnetes Ergebnis für $\overline{MR}$ einsetzen:
  $\overline{MO} = 0{,}6 \cdot \overline{MR} = 0{,}6 \cdot 7{,}00 \ \text{cm} = 4{,}20 \ \text{cm}.$
  Mit diesen beiden Ergebnissen berechnet sich die gesuchte Strecke $\overline{OR}$ zu:
  $\overline{OR} = \overline{MR} - \overline{MO} = 7{,}00 \ \text{cm} - 4{,}20 \ \text{cm} = 2{,}80 \ \text{cm}.$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Zur farbigen Gestaltung werden das Dreieck $M P O$ und die Figur, die durch die Kreisbögen $\overset\frown{DA}$ und $\overset\frown{AB}$ sowie die Strecke $[B D]$ begrenzt wird, silber eingefärbt. Berechnen Sie den Inhalt $A$ der silber eingefärbten Fläche.
  
  Wir wollen zunächst den Flächeninhalt des Dreiecks $M P O$ berechnen. Dessen Grundseite $\overline{OP}$ ist (indirekt) gegeben, denn nach Aufgabe (c) gilt
  $\displaystyle \overline{OP} = 0{,}6 \cdot \overline{QR} = 0{,}6 \cdot 5{,}2 \ \text{cm} = 3{,}12 \ \text{cm}.$
  Die Höhe $\overline{MG}$ hast du in Aufgabe c) berechnet. Es ist $\overline{MG} = 3{,}90 \ \text{cm}$ . Der Flächeninhalt ist also gegeben durch:
  $\def\arraystretch{2} \begin{array}{c} A_{\text{Dreieck}} &=& \dfrac{1}{2} \cdot \text{Grundseite} \cdot \text{Höhe}\\ &=& \dfrac{1}{2} \cdot \overline{MG} \cdot \overline{OP} \\ &=& \dfrac{1}{2} \cdot 3{,}90 \ \text{cm} \cdot 3{,}12 \ \text{cm} \\ &=& 6{,}08 \ \text{cm}^2. \end{array}$
  Jetzt musst du noch den Flächeninhalt der durch die Kreisbögen $\overset{\frown}{DA}$ und $\overset{\frown}{AB}$ sowie der Strecke $[B D]$ begrenzten Fläche berechnen.
  Dazu berechnet man zunächst die Fläche des Kreissektors mit Mittelpunkt $B$ und Radius $\overline{BD}$ . Der für diese Rechnung benötigte Winkel ist $\sphericalangle DBA = 60°$ . Dann ist der Flächeninhalt des Kreissektors gegeben durch:
  $A_{\text{Sektor}} = \dfrac{\sphericalangle DBA}{360°}\cdot \overline{BD}^2 \cdot \pi = \dfrac{60°}{360°} \cdot (6 \ \text{cm})^2 \cdot \pi = 6 \pi = 18{,}85 \ \text{cm}^2.$
  Das Gleiche machst du nun auch für den Kreissektor mit Mittelpunkt $D$ und Radius $\overline{BD}$ . Wir erhalten erneut:
  $A_{\text{Sektor}} = \dfrac{\sphericalangle ADB}{360°}\cdot \overline{BD}^2 \cdot \pi = \dfrac{60°}{360°} \cdot (6 \ \text{cm})^2 \cdot \pi = 6 \pi = 18{,}85 \ \text{cm}^2.$
  Bei diesem Vorgehen wird nun aber der Flächeninhalt des gleichseitigen Dreiecks $A B D$ doppelt berechnet. Dessen Flächeninhalt berechnet sich zu
  $\displaystyle A_{\text{Dreieck}} = \dfrac{1}{2} \cdot \overline{BD}^2 \cdot \sin(60°) = 15{,}59 \ \text{cm}^2$
  und muss einmal abgezogen werden. Insgesamt findest du damit also für die Fläche der beschriebenen Figur:
  $\def\arraystretch{1.25} \begin{array}{c} A_{\text{Figur}} &=& 2 \cdot A_{\text{Sektor}} - A_{\text{ABD}} + A_{\text{Dreieck}} \\ &=& 2 \cdot 18{,}85 \ \text{cm}^2 - 15{,}2 \ \text{cm}^2 + 6{,}08 \ \text{cm}^2 \\ &=& 28{,}19 \ \text{cm}^2. \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Bestimmen Sie rechnerisch den Umfang $u$ der Vorlage.
  $[$ Teilergebnis: $\sphericalangle OBA=100{,}54^\circ$ ; Ergebnis: $u=31{,}86\;\text{cm}$ $]$
  
  Der Abbildung kannst du entnehmen, dass für den Umfang $u$ allgemein gilt:
  $\displaystyle u = \underbrace{2 \cdot \underbrace{\dfrac{\sphericalangle OBA}{360°}\cdot 2\pi \cdot \overline{BC}}_{\text{Länge des Kreisbogens von } \overset{\frown}{AO}}}_{\text{Länge des Kreisbogens von } \overset{\frown}{AO} \text{ und } \overset{\frown}{AP}} + 2 \cdot \overline{OR} + \overline{RQ}.$
  Die einzige Größe, die in dieser Formel noch nicht gegeben oder berechnet wurde, ist der Winkel $\sphericalangle OBA$ . Ihn zu berechnen, funktioniert mithilfe des Kosinussatzes wie folgt:
  Wir betrachten das Dreieck $M B O$ . Der Kosinussatz lautet:
  $\displaystyle \overline{MO}^2 = \overline{MB}^2 + \overline{OB}^2 - 2 \cdot \overline{MO} \cdot \overline{MO} \cdot \cos(\sphericalangle OBM).$
  Du weißt bereits, dass $\overline{MO} = 4{,}20 \ \text{cm}$ und $\overline{BM} = 3{,}00 \ \text{cm}$ ist. Weiter ist $\overline{OB} = 6{,}00 \ \text{cm}$ , denn die Strecke $[O B]$ ist der Radius des Kreissektors und damit ist die Länge $\overline{OB} = \overline{BC} = 6 \ \text{cm}$ . Setzen wir diese Zahlenwerte in die Formel von oben ein und lösen nach $\cos(\sphericalangle OBM)$ auf, so erhalten wir:
  $\displaystyle \def\arraystretch{2} \begin{array}{c} (4{,}20 \ \text{cm})^2 &=& (3 \ \text{cm})^2 + (6 \ \text{cm})^2 - 2 \cdot 3 \ \text{cm} \cdot 6 \ \text{cm} \cdot \cos(\sphericalangle OBM) \\ 17{,}64 \ \text{cm}^2 &=& 9 \ \text{cm}^2 + 36 \ \text{cm}^2 - 36 \ \text{cm}^2 \cdot \cos(\sphericalangle OBM) \\ \cos(\sphericalangle OBM) &=& - \dfrac{17{,}64 \ \text{cm}^2 - 9 \ \text{cm}^2 - 36 \ \text{cm}^2 }{36 \ \text{cm}^2 } = 40{,}54°. \end{array}$
  Für unseren gesuchten Winkel $\sphericalangle{OBA}$ gilt schließlich:
  $\displaystyle \sphericalangle OBA = \sphericalangle OBM + 60° = 40{,}54° + 60° = 100{,}54°.$
  Damit kannst du nun den Umfang mithilfe der oben aufgestellten Formel berechnen. Der Umfang ist:
  $u = 2 \cdot \dfrac{100{,}54°}{360°} \cdot 2 \pi \cdot 6 \ \text{cm} + 2 \cdot 2{,}8 \ \text{cm} + 5{,}2 \ \text{cm} = 31{,}86 \ \text{cm}.$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. Das Firmenlogo wird später auf T-Shirts aufgenäht. Man geht davon aus, dass der benötigte Faden um $200\;\%$ länger als der Umfang der Vorlage ist. Auf einer Rolle befinden sich $500$ m Faden. Berechnen Sie, wie viele Firmenlogos mit einer Rolle höchstens aufgenäht werden können.
  Firmenlogos
  
  Der benötigte Faden ist gemäß Angabe um $200\;\%$ größer als der Umfang $u$ der Vorlage, das bedeutet, die benötigte Fadenlänge $l_{\text{Faden}}$ ist:
  $l_{\text{Faden}} = \dfrac{(100\;\% + 200\;\%) \cdot 31{,}86 \ \text{cm}}{100\;\%} = 95{,}58 \ \text{cm}.$
  Auf einer Rolle befinden sich $500$ m Faden. In cm entspricht dies einer Länge $l_{\text{Rolle}}$ von
  $\displaystyle l_{\text{Rolle}} = 500 \cdot 100 \ \text{cm} = 50\ 000 \ \text{cm}.$
  Um die Anzahl $N$ der Logos, die gedruckt werden können, zu berechnen, musst du nun den folgenden Quotienten berechnen:
  $\displaystyle N = \dfrac{l_{\text{Rolle}}}{l_{\text{Faden}}} = \dfrac{50\ 000 \ \text{cm}}{95{,}58 \ \text{cm}} = 523, 12 \approx 523.$
  Insgesamt können also $523$ Logos mit dem zur Verfügung stehenden Faden genäht werden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉