Nachtermin Teil A - lernen mit Serlo!

Auf Meereshöhe beträgt der Luftdruck unter normalen Bedingungen $1013\; \text{hPa}$ (Hektopascal). Mit zunehmender Höhe nimmt der Luftdruck ab.

Der Wert des Luftdrucks kann annähernd durch die Funktion $f$ mit der Gleichung $y=1013\cdot0{,}87^{x\;\;}$ $(\mathbb{G} = \mathbb{R}^+_0 \times \mathbb{R}^+_0)$ beschrieben werden, wobei $y$ den Luftdruck in $\text{hPa}$ und $x$ die Höhe in Kilometer über Meereshöhe angibt.

Unten ist der Graph zu dieser Funktion abgebildet.

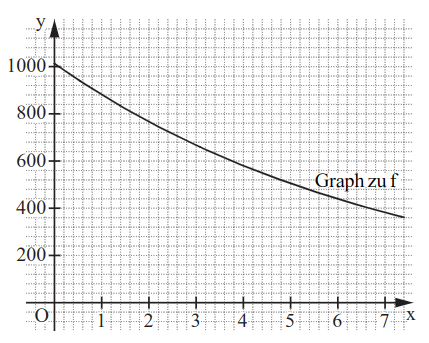
Geben Sie an, um wie viel Prozent der Luftdruck entsprechend dieser Funktion pro Kilometer Höhe sinkt.
%

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
Gesucht ist die Änderungsrate ( $\text{hPa}$ pro $\text{km}$ ) der Funktion $f$ . Diese kannst Du wie folgt aus der Funktionsgleichung $y=1013\cdot0{,}87^x$ ablesen:
Die Änderungsrate ist " $1 -$ Basis", d.h. $1-0{,}87=0{,}13$ .
Der Luftdruck sinkt also pro Kilometer Höhe um $13\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
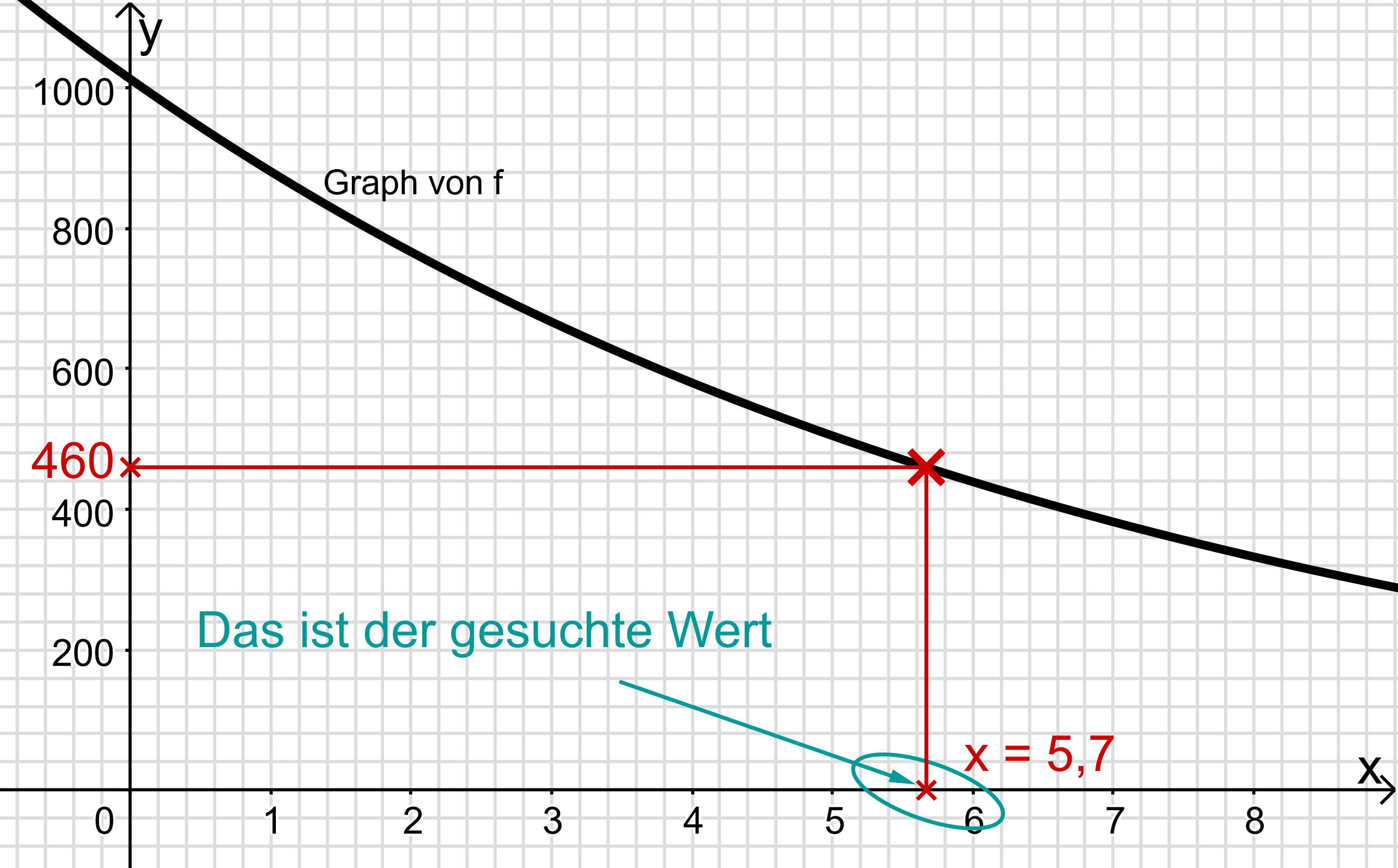
Der minimale Luftdruck, bei dem Menschen nachweislich dauerhaft leben können, liegt bei etwa $460 \;\text{hPa}$ . Ermitteln Sie mithilfe des Graphen, in welcher Höhe dieser minimale Luftdruck vorherrscht.
km

Die Frage ist: Welches $x$ (Höhe) muss man einsetzen, damit als $y$ -Wert (Luftdruck) $460$ rauskommt?
Um das herauszufinden, markierst du im Bild zunächst auf der $y$ -Achse den Wert $460.$ Als Nächstes markierst du den Punkt auf dem Graphen mit dieser $y$ -Koordinate. Von diesem Punkt liest Du schließlich die gesuchte $x$ -Koordinate ab.
Die Höhe, in der der Luftdruck $460\ \text{hPa}$ beträgt, ist also $5{,}7 \;\text{km}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
In der Luftfahrt verwendet man für den Zusammenhang zwischen Höhe und Luftdruck die Faustregel: „Alle $5{,}5 \;\text{km}$ halbiert sich der Luftdruck.“ Die momentane Reisehöhe eines Flugzeugs der Fluglinie „RisingAir“ liegt bei $11 \;\text{km}$ . Berechnen Sie, um wie viel Prozent der Wert des Luftdrucks entsprechend der Faustregel größer ist als der Funktionswert, der sich für diese Höhe ergibt. Runden Sie auf Ganze.
%
Hier benötigst du zusätzlich als Grundwissen: Prozentrechnung
Man unterteilt die Lösung dieser Aufgabe in drei Schritte:
Als erstes berechnet man den Luftdruck in der Höhe $11\; \text{km}$ mithilfe der Faustregel.
Dann berechnet man den Luftdruck in der Höhe $11\; \text{km}$ mithilfe der Funktion $f$ .
Schließlich rechnet man aus, um wie viel Prozent der Wert für den Luftdruck, den man mit der Faustregel erhalten hat, von dem Wert abweicht, den man mithilfe von $f$ erhalten hat.
1. Berechnung mit der Faustregel
Da $11 = 2\cdot5{,}5$ gilt, halbiert sich der Luftdruck zweimal:
Einmal nach $5{,}5$ Kilometern und dann noch einmal nach $5{,}5$ (also insgesamt $11$ ) Kilometern.
Insgesamt erhältst du also ein Viertel des Anfangswertes:
Das heißt: Der Luftdruck in der Höhe $11 \;\text{km}$ beträgt $253\;\text{hpa}$ .
2. Berechnung mit der Funktion
Dazu setzt du den $x$ -Wert $11$ in die Funktionsgleichung ein:
Der Luftdruck in $11\;\text{km}$ Höhe beträgt also $219\;\text{hPa}$ .
3. Berechnung der Abweichung in Prozent
Dazu setzt du die gegebenen Werte in die übliche Formel für Prozentrechnung ein.
Als Grundwert nimmst du $G = 219$ , da du wissen willst, um wie viel Prozent der Faustregelwert von diesem Wert abweicht.
Als Prozentwert nimmst du $W=253-219=34^{ }$ : Das ist der Unterschied zwischen den beiden Werten, die du vergleichen sollst.
Gesucht ist der Prozentsatz $p$ (also der prozentuale Unterschied zwischen $G$ und $W$ ). Die Formel liefert:
Der mit der Faustregel errechnete Luftdruck ist also um $16\;\%$ höher als der Wert, der sich aus der Funktion $f$ ergibt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

1. Berechnung mit der Faustregel

2. Berechnung mit der Funktion

3. Berechnung der Abweichung in Prozent

Hast du eine Frage oder Feedback?