Nachtermin Teil A - lernen mit Serlo!

Die freie Lernplattform

Nebenstehende Skizze zeigt das rechtwinklige Dreieck $ABC$ mit der Hypotenuse $[AC]$ . $M$ ist der Mittelpunkt der Strecke $[AB]$ .

Punkte $P_n$ liegen auf der Strecke $[AC]$ mit $\overline{AP_n}=\textrm{x}\,\textrm{cm}\;(\textrm{x}\in\mathbb{R};\textrm{x}\in]0;10{,}86[)$ .

Es gilt: $\overline{AB}=9\;\textrm{cm};\measuredangle{BAC}=34°;\measuredangle{BMP_1}=70°.$

Bild

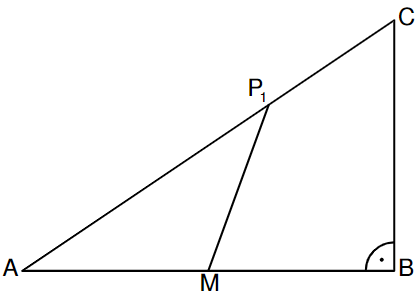
Berechnen Sie die Längen der Strecken $[AC_1]$ und $[AP_1]$ .
Runden Sie auf zwei Stellen nach dem Komma.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie (Kosinus), Sinussatz, Nebenwinkel, Innenwinkelsumme im Dreieck
Teilaufgabe a
Länge der Strecke $[AC]$ :
Das Dreieck ABC ist rechtwinklig: daher können wir den Kosinus verwenden:
$\cos(\alpha)=\dfrac{\text{Ankathete}}{\text{Hypotenuse}}$
$\cos(34°)=\dfrac{9\,\text{cm}}{\overline{AC}}$
$\overline{AC}=\dfrac{9\;\text{cm}}{\cos(34°)}\approx10{,}86\;\textrm{cm}$
Länge der Strecke $AP_1$ :
$\measuredangle P_1MA=180°-70°=110°$ (Nebenwinkel).
$\measuredangle MP_1A=180°-110°-34°=36°$ (Innenwinkelsumme im Dreieck)
Sinussatz:
$\frac{a}{\sin\left(\alpha\right)}=\frac{b}{\sin\left(\beta\right)}$
$\frac{\overline{AM}}{\sin\left(36°\right)}=\frac{\overline{AP_1}}{\sin\left(110°\right)}$
$\overline{AP_1}=\frac{\overline{AM}\cdot\sin\left(110°\right)}{\sin\left(36°\right)}$
$\overline{AP_1}=\frac{4{,}5\;\textrm{cm}\cdot\sin\left(110°\right)}{\sin\left(36°\right)}\approx7{,}19\;\text{cm}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Begründen Sie, weshalb für alle Punkte $P_n$ gilt: $\measuredangle BMP_n+\measuredangle MP_nC=214°$ .

Teilaufgabe b
$\measuredangle BMP_n+\measuredangle MP_nC=214°:$
$\measuredangle MP_1C=180°-36°=144°$ (Nebenwinkel)
$\measuredangle BMP_n+\measuredangle MP_nC\ =70°+144°=214°$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.