Wahlteil - CAS - lernen mit Serlo!

Aufgabe 3B

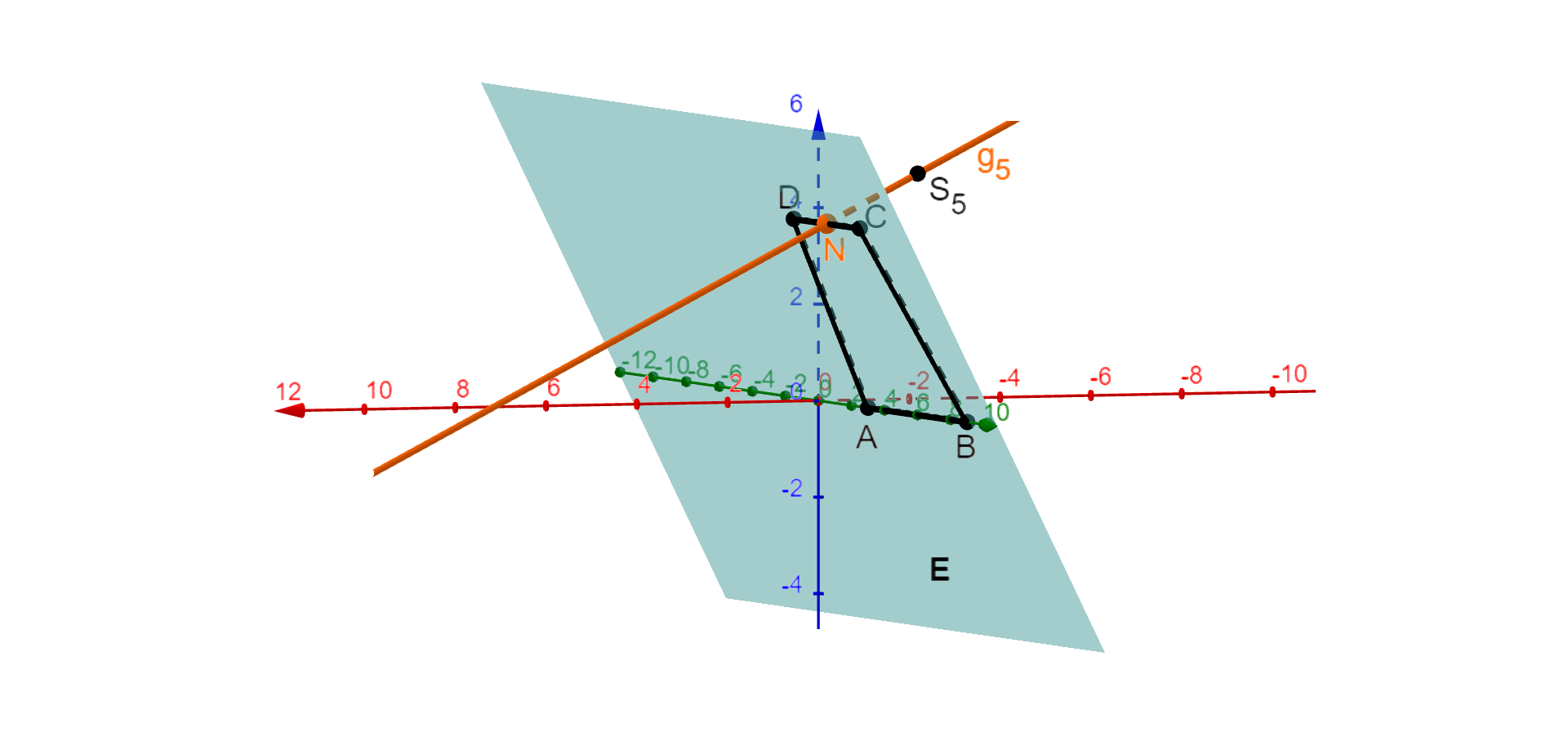
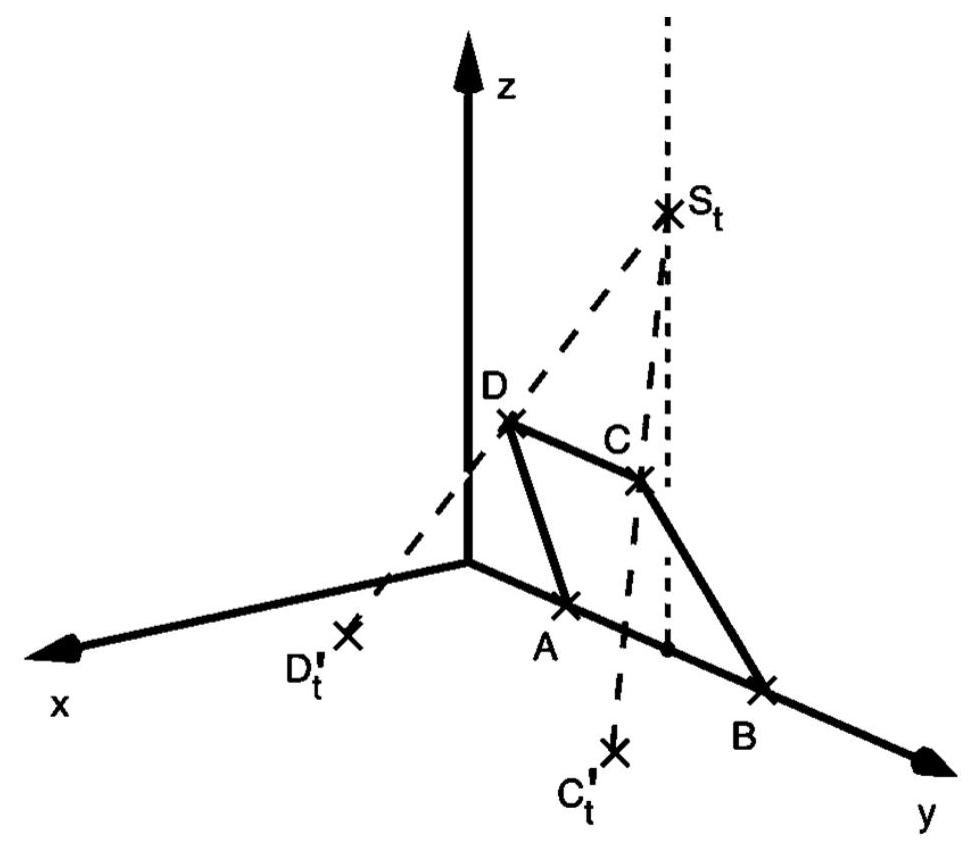
Die Abbildung 1 zeigt das Viereck $A B C D$ mit $A (0 | 3 | 0), B (0 | 9 | 0), C (2 | 8 | 4)$ und $D (2 | 4 | 4)$ . Gegeben sind außerdem die Punkte $S_{t} (0 | 6 | t)$ mit $t \geq 0$ .

Weisen Sie nach,
- dass in dem Viereck $A B C D$ zwei Seiten parallel zueinander sind.
- dass in dem Viereck $A B C D$ zwei gegenüberliegende Seiten gleich lang sind.
- dass das Viereck $A B C D$ kein Rechteck ist.
(6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Viereck
Lösung
In dem Viereck ABCD sind zwei Seiten parallel zueinander
Gegeben sind $A (0 | 3 | 0)$ , $B (0 | 9 | 0)$ , $C (2 | 8 | 4)$ und $D (2 | 4 | 4)$ .
Bei den Punkten $A$ und $B$ und ebenso bei den Punkten $C$ und $D$ stimmen die
$x_{1}$ -Koordinaten und die $x_{3}$ -Koordinaten überein. Somit ist $A B ∥ C D$ .
In dem Viereck ABCD sind zwei gegenüberliegende Seiten gleich lang
Berechne die Vektoren $\vec{A D}$ und $\vec{B C}$ .
$\vec{A D} = (\begin{array}{c} 2 \\ 4 \\ 4 \end{array}) - (\begin{array}{c} 0 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} 2 \\ 1 \\ 4 \end{array})$
$\vec{B C} = (\begin{array}{c} 2 \\ 8 \\ 4 \end{array}) - (\begin{array}{c} 0 \\ 9 \\ 0 \end{array}) = (\begin{array}{c} 2 \\ - 1 \\ 4 \end{array})$
Da bei beiden Vektoren die Koordinaten jeweils den gleichen Betrag haben, sind die Beträge der Vektoren gleich groß.
$| \vec{A D} | = | \vec{B C} |$
Das Viereck ABCD ist kein Rechteck
Berechne das Skalarprodukt zwischen den Vektoren $\vec{A B}$ und $\vec{A D}$ . Prüfe damit, ob die beiden Vektoren senkrecht aufeinander stehen.
$\vec{A D} = (\begin{array}{c} 2 \\ 1 \\ 4 \end{array})$
$\vec{A B} = (\begin{array}{c} 0 \\ 9 \\ 0 \end{array}) - (\begin{array}{c} 0 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} 0 \\ 6 \\ 0 \end{array})$
$\vec{A D} \circ \vec{A B} = (\begin{array}{c} 2 \\ 1 \\ 4 \end{array}) \circ (\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) = 2 \cdot 0 + 1 \cdot 6 + 4 \cdot 0 = 6 \neq 0$
Die beiden Vektoren stehen nicht senkrecht aufeinander, d.h. das Viereck $A B C D$ ist kein Rechteck.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
In dem Viereck $A B C D$ sind zwei Seiten parallel zueinander.
Betrachte bei den Punkten $A$ und $B$ und ebenso bei den Punkten $C$ und $D$ übereinstimmende Koordinaten.
In dem Viereck $A B C D$ sind zwei gegenüberliegende Seiten gleich lang.
Berechne die Vektoren $\vec{A D}$ und $\vec{B C}$ .
Das Viereck $A B C D$ ist kein Rechteck.
Prüfe mit dem Skalarprodukt, ob die beiden Vektoren $\vec{A B}$ und $\vec{A D}$ senkrecht aufeinander stehen.
Bestimmen Sie eine Gleichung der Ebene $E$ , in der das Viereck $A B C D$ liegt, in Koordinatenform. (3 BE)
[Zur Kontrolle: $2 x - z = 0$ ]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parameterform in Koordinatenform
Ebene in Parameterform
$E : \vec{x} = \vec{O A} + r \cdot \vec{A B} + s \cdot \vec{A D} = (\begin{array}{c} 0 \\ 3 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 1 \\ 4 \end{array})$
Umwandlung in Normalenform
Berechne den Normalenvektor $\vec{n}$ der Ebene $E$ :
$\vec{n} = (\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) \times (\begin{array}{c} 2 \\ 1 \\ 4 \end{array}) = (\begin{array}{c} 24 \\ 0 \\ - 12 \end{array}) = 12 \cdot (\begin{array}{c} 2 \\ 0 \\ - 1 \end{array})$
$E : (\vec{x} - (\begin{array}{c} 0 \\ 3 \\ 0 \end{array})) \circ (\begin{array}{c} 2 \\ 0 \\ - 1 \end{array}) = 0$
Berechne das Skalarprodukt:
$E : 2 \cdot x + 0 \cdot y + (- 1) \cdot z - (0 + 0 + 0) = 0 \Rightarrow 2 \cdot x - z = 0$
Das Viereck liegt in der Ebene $2 \cdot x - z = 0$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Erstelle eine Ebenengleichung in Parameterform und wandle sie in die Koordinatenform um.
Berechnen Sie den Winkel zwischen der $x y$ -Ebene und der Ebene $E$ , in der das Viereck $A B C D$ liegt. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen Vektoren, Geraden und Ebenen
Winkel zwischen der xy-Ebene und der Ebene E
Der Normalenvektor der xy-Ebene ist ${\vec{n}}_{x y} = (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$ und der Normalenvektor der Ebene $E$ ist ${\vec{n}}_{E} = (\begin{array}{c} 2 \\ 0 \\ - 1 \end{array})$ .
Dann folgt für den Winkel zwischen zwei Ebenen:
$\cos α = \frac{| {\vec{n}}_{E} \circ {\vec{n}}_{x y} |}{| {\vec{n}}_{E} | \cdot | {\vec{n}}_{x y}} = \frac{| (\begin{array}{c} 2 \\ 0 \\ - 1 \end{array}) \circ (\begin{array}{c} 0 \\ 0 \\ 1 \end{array}) |}{\sqrt{2^{2} + 0^{2} + (- 1)^{2}} \cdot 1} = \frac{| - 1 |}{\sqrt{5}}$
$α = \cos^{- 1} (\frac{1}{\sqrt{5}}) \approx {63,4}^{\circ}$
Der Winkel zwischen der xy-Ebene und der Ebene $E$ beträgt rund ${63,4}^{\circ}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Benutze die beiden Normalenvektoren der beiden Ebenen und berechne den Winkel mit $\cos α = \frac{| {\vec{n}}_{E} \circ {\vec{n}}_{x y} |}{| {\vec{n}}_{E} | \cdot | {\vec{n}}_{x y}}$
Betrachtet werden die Geraden $g_{t}$ , die senkrecht zu der Ebene $E$ liegen und durch die Punkte $S_{t}$ verlaufen.
Ermitteln Sie diejenigen Werte von $t$ , für die der Schnittpunkt der zugehörigen Geraden $g_{t}$ und der Ebene $E$ im Inneren des Vierecks $A B C D$ liegt. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
Lösung
Geraden $g_{t}$ , die senkrecht zu der Ebene $E$ liegen und durch die Punkte $S_{t}$ verlaufen
Der Normalenvektor der Ebene $E$ ist ${\vec{n}}_{E} = (\begin{array}{c} 2 \\ 0 \\ - 1 \end{array})$ $\Rightarrow$ $g_{t} : \vec{x} = \vec{O S_{t}} + r \cdot {\vec{n}}_{E} = (\begin{array}{c} 0 \\ 6 \\ t \end{array}) + r \cdot (\begin{array}{c} 2 \\ 0 \\ - 1 \end{array})$
Werte von $t$ , für die der Schnittpunkt der zugehörigen Geraden $g_{t}$ und der Ebene $E$ im Inneren des Vierecks $A B C D$ liegt
$g_{t} \cap E$ :
$2 \cdot (0 + 2 r) - (t - r)$ $=$ $0$
↓
Löse die Klammer auf.
$4 r - t + r$ $=$ $0$ $+ t$
$5 r$ $=$ $t$ $: 5$
$r$ $=$ $\frac{1}{5} t$
Eingesetzt in $g_{t}$ :
$\vec{O S_{t}} = (\begin{array}{c} 0 \\ 6 \\ t \end{array}) + \frac{1}{5} t \cdot (\begin{array}{c} 2 \\ 0 \\ - 1 \end{array}) = (\begin{array}{c} \frac{2}{5} t \\ 6 \\ t - \frac{1}{5} t \end{array}) = (\begin{array}{c} \frac{2}{5} t \\ 6 \\ \frac{4}{5} t \end{array})$
$\Rightarrow S_{t} (\frac{2}{5} t | 6 | \frac{4}{5} t)$
Die x-Koordinate des Rechtecks läuft von $0$ bis $2$ .
Demnach muss für die x-Koordinaten der Schnittpunkte gelten:
$0 < \frac{2}{5} t < 2$ oder $0 < t < 5$ .
Gilt $0 < t < 5$ , dann liegt der Schnittpunkt der zugehörigen Geraden $g_{t}$ und der Ebene $E$ im Inneren des Vierecks $A B C D$ .
Anmerkung: Die folgende Abbildung ist in der Aufgabenstellung nicht gefordert. Die dient nur zur Veranschaulichung.
Dargestellt ist hier das Viereck $A B C D$ , die Ebene $E$ , der Punkt $S_{5}$ und die zu $E$ senkrechte Gerade $g_{5}$ .
Die obere Kante des Rechtecks wird von der Gerade $g_{5}$ in der Mitte geschnitten (Punkt $N$ ).
In diesem Fall liegt der Schnittpunkt der Geraden $g_{5}$ und der Ebene $E$ nicht im Inneren des Vierecks $A B C D$ . Erst, wenn $0 < t < 5$ ist, wird das Viereck im Innern geschnitten.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Erstelle mit dem Normalenvektor der Ebene $E$ und dem Punkt $S_{t}$ die Gleichung der Geraden $g_{t}$ .
Schneide $g_{t}$ mit $E$ und berechne die Koordinaten $S_{t}$ des Schnittpunktes.
Überlege, welche x-Koordinatenwerte das Viereck $A B C D$ annehmen kann. Schließe daraus auf die möglichen t-Werte.
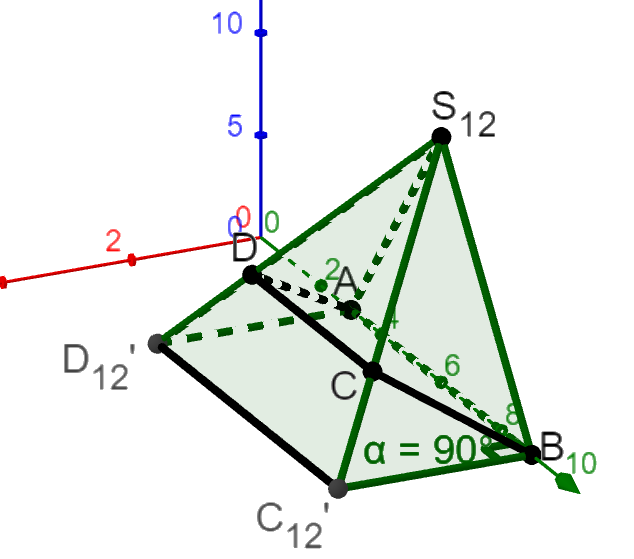
Im Folgenden gilt $t > 4$ .
Die Gerade durch die Punkte $S_{t}$ und $C$ schneidet die $x y$ -Ebene im Punkt $C_{t}^{'}$ , die Gerade durch die Punkte $S_{t}$ und $D$ schneidet diese Ebene im Punkt $D_{t}^{'}$ (vgl. Abbildung 1).
Die beiden folgenden Gleichungen I und II liefern gemeinsam einen bestimmten Wert von $t$ .
I. $\vec{O S_{t}} + r \cdot \vec{S_{t} C} = \vec{O C_{t}^{'}}$ mit $C_{t}^{'} (x | y | 0)$
II. $\vec{B A} \cdot \vec{B C_{t}^{'}} = 0$
Geben Sie für diesen Wert von $t$ die Art des Vierecks $A B C_{t}^{'} D_{t}^{'}$ an und begründen Sie Ihre Angabe. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Art des Vierecks $A B C_{t}^{'} D_{t}^{'}$
Es handelt sich um ein Rechteck.
Begründung
Aus Gleichung $II \vec{B A} \cdot \vec{B C_{t}^{'}} = 0$ folgt, dass die beiden Vektoren senkrecht aufeinander stehen.
Weiterhin ist das Viereck $A B C D$ symmetrisch zur Ebene $E_{1} : y = 6$ .
Der Punkt $S_{t}$ liegt ebenfalls in der Ebene $E_{1}$ . Aus Symmetriegründen liegt der Punkt $D_{t}^{'}$ symmetrisch zu $C_{t}^{'}$ (bezüglich der Ebene $E_{1}$ ).
Ebenso liegt der Punkt $A$ symmetrisch zum Punkt $B$ . Dann steht auch $A D_{t}^{'}$ senkrecht zu $A B$ und es ist $C_{t}^{'} D_{t}^{'}$ parallel zu $A B$ .
Die folgende Abbildung ist in der Aufgabenstellung nicht gefordert. Die dient nur zur Veranschaulichung.
Der eingezeichnete Winkel im Rechteck $A B C_{t}^{'} D_{t}^{'}$ ist ein rechter Winkel.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Betrachte Gleichung II. Was folgt aus dieser Gleichung?
Beachte, dass das Viereck $A B C D$ symmetrisch zur Ebene $E_{1} : y = 6$ ist und dass der Punkt $S_{t}$ ebenfalls in der Ebene $E_{1}$ liegt.
Was folgt dann aus Symmetriegründen?
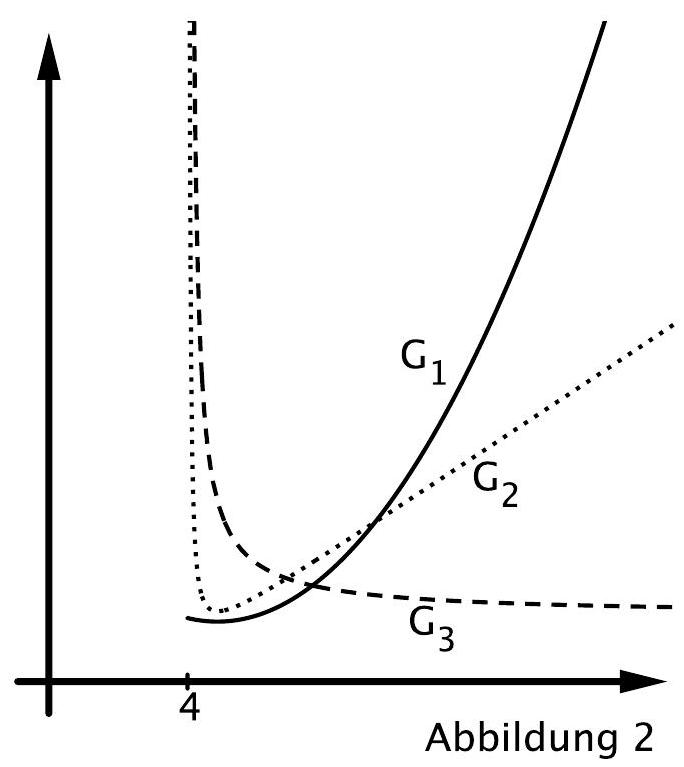
Das Volumen der Pyramide $A B C_{t}^{'} D_{t}^{'} S_{t}$ wird in Abhängigkeit von $t$ durch einen der drei abgebildeten Graphen $G_{1}, G_{2}$ und $G_{3}$ dargestellt (Abbildung 2).
Geben Sie diesen Graphen an und begründen Sie Ihre Angabe. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Richtiger Graph
Der Graph $G_{2}$ gehört zu dem Pyramidenvolumen $A B C_{t}^{'} D_{t}^{'} S_{t}$ in Abhängigkeit von $t$ .
Begründung
Das Pyramidenvolumen berechnet sich mit $V = \frac{1}{3} \cdot G \cdot h$ .
In diesem Fall ist das Pyramidenvolumen $V (t) = \frac{1}{3} \cdot G (t) \cdot t$ für $t > 4$ .
Es besteht folgender Zusammenhang:
Nähert sich $t$ dem Wert $4$ , wird $G (t)$ beliebig groß, während die Höhe größer als $4$ ist. $\Rightarrow V \mapsto \infty$
Für $t \mapsto \infty$ wird die Höhe beliebig groß, während $G (t)$ immer kleiner wird und sich dem Flächeninhalt eines Rechtecks mit den Eckpunkten $A, B, (2 | 8 | 0)$ und $(2 | 4 | 0)$ nähert. $\Rightarrow V \mapsto \infty$
Es passt also nur Graph $G_{2}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für das Pyramidenvolumen gilt $V (t) = \frac{1}{3} \cdot G (t) \cdot t$ für $t > 4$ .
Untersuche, wie sich das Volumen verändert, wenn $t \mapsto 4$ geht bzw. wenn $t \mapsto \infty$ geht.
Schließe dann auf den passenden Graphen.

Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen → Was bedeutet das?

$2 \cdot (0 + 2 r) - (t - r)$	$=$	$0$
	↓	Löse die Klammer auf.
$4 r - t + r$	$=$	$0$	$+ t$
$5 r$	$=$	$t$	$: 5$
$r$	$=$	$\frac{1}{5} t$

Aufgabe 3B

Lösung

Hast du eine Frage oder Feedback?

Ebene in Parameterform

Umwandlung in Normalenform

Hast du eine Frage oder Feedback?

Winkel zwischen der xy-Ebene und der Ebene E

Hast du eine Frage oder Feedback?

Lösung

Hast du eine Frage oder Feedback?

Art des Vierecks ABCt′Dt′

Begründung

Hast du eine Frage oder Feedback?

Richtiger Graph

Begründung

Hast du eine Frage oder Feedback?

Art des Vierecks $A B C_{t}^{'} D_{t}^{'}$