Abiturprüfungen Mathe eA mit Lösungen

Aufgabe 1A

Auf einer Autobahn entsteht morgens an einer Baustelle häufig ein Stau, der sich dann wieder vollständig auflöst. An einem bestimmten Tag wird die momentane Änderungsrate der Staulänge für $0 \leq x \leq 4$ mithilfe der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)=x \cdot(8-5 x) \cdot\left(1-\frac{x}{4}\right)^{2}$ beschrieben.

Dabei gibt $x$ die nach 06: 00 Uhr vergangene Zeit in Stunden und $f(x)$ die momentane Änderungsrate der Staulänge in Kilometer pro Stunde $\left(\frac{\mathrm{km}}{\mathrm{h}}\right)$ an.

Nennen Sie die Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat.
Begründen Sie anhand der Struktur des Funktionsterms von $f$ , dass es keine weiteren solchen Zeitpunkte gibt. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat
Setze $f(x)$ gleich null:
$0=x\cdot (8-5x)\cdot \left(1-\dfrac{x}{4}\right)^2$
Es wird der Satz vom Nullprodukt angewendet:
Es ist $x=0$ oder $8-5x=0$ oder $\left(1-\dfrac{x}{4}\right)^2=0$ .
Also ist $x=0$ und/oder $x=\dfrac{8}{5}=1{,}6$ und/oder $x=4$ .
Zu diesen x-Werten gehören die Uhrzeiten $6:00$ Uhr, $7:36$ Uhr und $10:00$ Uhr.
Die momentane Änderungsrate der Staulänge ist zu diesen Zeiten gleich null.
Begründung mit dem Funktionsterm
Die Funktion $f$ hat den Grad $4$ , d.h. der Graph der Funktion hat maximal vier einfache Nullstellen.
Die ersten beiden Nullstellen sind einfache Nullstellen.
$x=4$ ist eine doppelte Nullstelle. Es gibt also insgesamt vier Nullstellen.
Somit gibt es keine weiteren Nullstellen und keine weiteren Zeitpunkte, an denen die momentane Änderungsrate der Staulänge den Wert null hat.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Nullstellen der Funktion $f$ .
Für die Begründung muss die Vielfachheit der Nullstellen diskutiert werden und der Grad des Polynoms.
Bestimmen Sie den Zeitpunkt, zu dem die Staulänge am stärksten zunimmt.
Zeigen Sie, dass der zugehörige Wert der momentanen Änderungsrate etwa $2{,}2$ $\frac{\mathrm{km}}{\mathrm{h}}$ beträgt. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
Maximale Änderungsrate
Gesucht ist der Hochpunkt des Graphen der Funktion $f$ .
Definiere auf dem CAS die Funktion $f(x)$ .
Definiere die 1. Ableitung $t(x)=\dfrac{d}{dx}\left(f(x)\right)$ .
Löse mit nSolve die Gleichung $t(x)=0$ .
Dies muss man mehrfach durchführen und man erhält die Werte
$x_1=0{,}6202041, x_2=2{,}579796$ und $x_3=4$ .
Wo liegt die stärkste Zunahme?
Betrachte die Steigung links und rechts von $x=0{,}62$ (Vorzeichenwechselkriterium).
$f'(0)=(5\cdot 0^2- 16\cdot 0 +8)\cdot\left(1-\dfrac{0}{4}\right)=8$
$f'(1)=(5 \cdot 1^2- 16\cdot 1 +8)\cdot\left(1-\dfrac{1}{4}\right)=-\dfrac{9}{4}$
Es findet also ein Vorzeichenwechsel von $+\rightarrow -$ statt.
Der gesuchte Hochpunkt liegt also bei $x=0{,}62$ .
Zu dem $x$ -Wert $0{,}62$ gehört die Uhrzeit $6:37$ Uhr.
Somit nimmt die Staulänge um $6:37$ Uhr am stärksten zu.
Anmerkung
Da beim ersten Wert $x_1$ ein Hochpunkt vorliegt, muss beim zweiten Wert $x_2$ ein Tiefpunkt liegen. Beim dritten Wert $x_3=4$ ist $f(4)=0$ .
Wert der momentanen Änderungsrate zur Zeit der stärksten Zunahme
Berechne $f(0{,}62)=(8\cdot 0{,}62-5\cdot0{,}62^2)\cdot\left(1-\dfrac{0{,}62}{4}\right)^2\approx2{,}2$
Der Wert der momentanen Änderungsrate beträgt etwa $2{,}2$ $\frac{\mathrm{km}}{\mathrm{h}}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne den Hochpunkt des Graphens der Funktion $f$ .
Geben Sie den Zeitpunkt an, zu dem der Stau am längsten ist.
Begründen Sie Ihre Angabe. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Maximale Staulänge
Die maximale Staulänge wird erreicht, wenn die Funktion $f$ (die momentane Änderungsrate) die x-Achse schneidet. Hier wechselt $f$ vom Positiven ins Negative. Dieser Zeitpunkt wurde schon in Aufgabe a) berechnet. Es ist $x=1{,}6$ .
Um $7:36$ Uhr ist die Staulänge maximal.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Gesucht ist der Schnittpunkt von $f$ mit der x-Achse, d.h. die Stelle, an der $f$ vom Positiven ins Negative wechselt.
Gegeben ist die in $\mathbb{R}$ definierte Funktion $s$ mit $s(x)=\left(\frac{x}{4}\right)^{2} \cdot(4-x)^{3}$ . $s$ ist eine Stammfunktion von $f$ .
Der Stau entsteht um 06: 00 Uhr.
Begründen Sie, dass die folgende Aussage richtig ist:
Für den Zeitraum von 06: 00 Uhr bis 10: 00 Uhr kann die Staulänge durch die Funktion $s$ angegeben werden.
Prüfen Sie, ob sich der Stau um 10: 00 Uhr vollständig aufgelöst hat. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Die Staulänge kann für jeden Zeitpunkt von $6:00$ Uhr bis $10:00$ Uhr durch die Funktion $s$ angegeben werden.
$s$ ist eine Stammfunktion von $f$ .
Somit gilt: $\displaystyle\int_0^t f(x)dx=s(t)-s(0)$
Es gilt außerdem: $s'(x)=f(x)$ .
Weiterhin ist: $s(0)=\left(\dfrac{0}{4}\right)^2\cdot (4-0)^3=0\cdot 4^3=0$
Die Staulänge um $6:00$ Uhr ist gleich null, d.h. hier beginnt gerade der Stau.
Um $10:00$ Uhr ist $x=4$ und $s(4)=\left(\dfrac{4}{4}\right)^2\cdot (4-4)^3=1\cdot 0^3=0$ , d.h. der Stau hat sich aufgelöst.
Somit kann die Staulänge durch die Funktion $s$ angegeben werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Prüfe, ob $s(0)=s(4)=0$ ist.
Berechnen Sie die Zunahme der Staulänge von 06:00 Uhr bis 07:30 Uhr und geben Sie für diesen Zeitraum die durchschnittliche Änderungsrate der Staulänge an. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Integral
Zunahme der Staulänge
Um $6:00$ Uhr ist $x=0$ und um $7:30$ Uhr ist $x=1{,}5$ .
Berechnet werden muss also das Integral:
Der Stau hat von $6:00$ Uhr bis $7:30$ Uhr um rund $2{,}2\;\text{km}$ zugenommen.
Mittlere Änderungsrate der Staulänge für diesen Zeitraum
Berechne $\dfrac{1}{1{,}5-0}\displaystyle\int_0^{1{,}5}f(x) dx=\dfrac{s(1{,}5)-s(0)}{1{,}5}=\dfrac{2{,}197}{1{,}5}\approx1{,}46$
Die mittlere (durchschnittliche) Änderungsrate der Staulänge für diesen Zeitraum beträgt rund $1{,}5\;\dfrac{\text{km}}{\text{h}}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne das Integral über die Funktion $f$ im angegebenen Zeitraum und anschließend den Mittelwert.

Betrachtet wird die Schar der in $\mathbb{R}$ definierten Funktionen $h_{k}$ mit $h_{k}(x)=(x-3)^{k}+1$ und $k \in \mathbb{N}, k>0$ .

Ermitteln Sie die Koordinaten derjenigen Punkte, die alle Graphen der Schar gemeinsam haben. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt zweier Funktionen

Gleichsetzen der Funktionen

Zur Berechnung des Schnittpunktes setze $h_{k_1}=h_{k_2}$ :

$\displaystyle (x-3)^{k_1}+1$	$=$	$\displaystyle (x-3)^{k_2}+1$	$\displaystyle -1$
$\displaystyle (x-3)^{k_1}$	$=$	$\displaystyle (x-3)^{k_2}$

Diese Gleichung hat die Lösung $x_1=3$ , denn $0^{k_1}=0^{k_2}$ für $k_1,k_2 \in\{1; 2; 3...\}$ .

Der Funktionswert für $x=3$ ist $h_k(3)=(3-3)^{k}+1=0+1=1$

$\Rightarrow\;P_1(3|1)$

Für $x\neq 3$ folgt:

$\displaystyle (x-3)^{k_1}$	$=$	$\displaystyle (x-3)^{k_2}$	$\displaystyle :(x-3)^{k_2}$
	↓	Da $x\neq 3$ ist, darf durch $(x-3)^{k_2}$ geteilt werden.
$\displaystyle \dfrac{(x-3)^{k_1}}{(x-3)^{k_2}}$	$=$	$\displaystyle 1$
	↓	Wende ein Potenzgesetz an.
$\displaystyle (x-3)^{k_1-k_2}$	$=$	$\displaystyle 1$

Es ist $k_1\neq k_2$ :

Da $k_1\neq k_2$ kann der Exponent nicht null werden. Eine weitere Lösung findet man nur, wenn $x-3=1$ ist, da $1 ^{k_1-k_2}=1$ ist für $k_1,k_2 \in\{1; 2; 3...\}$ und $k_1=k_2+1$ .

$x-3=1\;\Rightarrow\;x_2=4$

Gemeinsame Punkte

Der Funktionswert für $x=4$ ist $h_k(4)=(4-3)^{k}+1=1+1=2$

$\Rightarrow\;P_2(4|2)$

Es gibt also zwei Punkte $P_1(3|1)$ und $P_2(4|2)$ , die alle Graphen der Schar gemeinsam haben.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Der Graph von $h_{5}$ und die Gerade durch die Punkte $P(3 \mid 1)$ und $Q(4 \mid 2)$ schließen zwei Flächenstücke ein.
Bestimmen Sie das Volumen des Körpers, der entsteht, wenn man diese beiden Flächenstücke um die $x$ -Achse rotieren lässt. (7 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationsvolumen
Lösung
Die Funktion $h_5$ ist gegeben durch:
$h_5(x)=(x-3)^5+1$
Geradengleichung $g$
Die beiden Punkte $P(3|1)$ und $Q(4|2)$ liegen auf einer Geraden $g$ .
$g(x)=m\cdot x+b$ mit $m=\dfrac{2-1}{4-3}=1\;\Rightarrow\;g(x)=1\cdot x+b$
Setze den z. B. den Punkt $P(3|1)$ ein:
$1=1\cdot 3+b\;\Rightarrow\;b=-2$
Die Gerade hat die Gleichung $g(x)=x-2$ .
Rotationsvolumen
Für die Volumenberechnung müssen die Schnittpunkte zwischen $h_5(x)$ und $g(x)$ bestimmt werden.
Setze $h_5(x)=g(x)$ und löse mit dem CAS die Gleichung $(x-3)^5+1=x-2$ .
Es werden drei Lösungen angegeben: $x_1=2, x_2=3$ und $x_3=4$ .
Somit kann der Rotationskörper berechnet werden.
Beachte jeweils, welche Funktion im Integrationsintervall größer ist.
Für $x\in]2;3[$ ist $h_5(x)>g(x)$ , denn $h_5(2{,}5)=(2{,}5-3)^5+1\approx0{,}97$ und $g(2{,}5)=2{,}5-2=0{,}5$ .
Für $x\in]3;4[$ ist $h_5(x)<g(x)$ , denn $h_5(3{,}5)=(3{,}5-3)^5+1\approx1{,}03$ und
$g(3{,}5)=3{,}5-2=1{,}5$ .
Allgemein gilt für den Rotationskörper: $V=\pi\displaystyle\int_a^bf(x)^2dx$
Somit erhält man:
Für das 1. Integral liefert der CAS-Rechner den gerundeten Wert $1{,}333$ und für das 2. Integral erhält man $2{,}856$ .
Das Gesamtrotationsvolumen beträgt demnach:
$V_{ges}=1{,}333+2{,}856=4{,}189\;\text{VE}\approx4{,}2\;\text{VE}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme die Geradengleichung durch die beiden gegebenen Punkte.
Berechne die Schnittpunkte zwischen der Geraden und dem Graphen der Funktion $h_5(x)$ .
Wende die Volumenformel für Rotationskörper an.
Beurteilen Sie die Gültigkeit der folgenden Aussage: (6 BE)
Es gibt genau einen Wert von $k$ , für den der Graph von $h_{k}^{\prime}$ Tangente an den Graphen von $h_{k}$ ist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Wert von $k$ ⁣, für den der Graph von $h_k'$ Tangente an den Graphen von $h_k$ ist
Berechne die erste Ableitung von $h_k$ :
$h_k(x)=(x-3)^{k}+1$
$\Rightarrow\;h_k'(x)=k\cdot(x-3)^{k-1}$
Wenn $h_k'$ Tangente sein soll, dann muss der Graph von $h_k'$ eine Gerade sein.
1. Fall
Die Gerade ist eine Parallele zur $x$ -Achse $(m=0)$ . Dann ist der Exponent von $h_k'(x)$ gleich null. $\Rightarrow\;$ $k-1=0$ bzw. $k=1$ .
Die Funktion $h_1(x)=(x-3)^1+1=x-2$ ist ebenfalls eine Gerade mit der Steigung $m=1$ .
$h_1'(x)$ ist keine Tangente an den Graphen von $h_1$ , da die Steigungen unterschiedlich sind.
2. Fall
Der Exponent von $h_k'(x)$ ist gleich eins.
$\Rightarrow\;k-1=1$ bzw. $k=2$
Die Funktion $h_2(x)=(x-3)^{2}+1$ hat die Ableitungsfunktion $h_2'(x)=2\cdot(x-3)=2x-6$ (Gerade mit der Steigung $2$ ).
Wenn der Graph von $h'_2$ Tangente der Funktion $h_2(x)$ sein soll, müssen sich beide Graphen in einem Punkt schneiden und der Graph von $h_2$ müsste dort die Steigung $2$ haben.
Setze die Funktionsterme gleich:
$\Rightarrow\;(x-3)^2+1=2x-6$
Der CAS-Rechner liefert als Lösung dieser Gleichung $x=4$ .
Für $x=4$ erhält man den y-Wert $h_2'(4)=2\cdot 4-6=2$ .
Beide Graphen schneiden sich im Punkt $B(4|2)$ und die beiden Graphen haben für $x=4$ die gleiche Steigung $h'_2(4)=2$ .
$\Rightarrow\;h_2'(x)$ ist Tangente an $h_2(x)$ im Punkt $B(4|2)$ .
Da $k=2$ die einzige Lösung ist, gibt es also genau einen Wert von $k$ ⁣, für den der Graph von $h_k'$ Tangente an den Graphen von $h_k$ ist.
Die Aussage ist also richtig.
Die folgende Abbildung dient nur zur Veranschaulichung.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die 1. Ableitung von $h_k(x)$ .
Wenn $h_k'$ Tangente sein soll, dann muss der Graph von $h_k'$ eine Gerade sein.
Untersuche die möglichen Fälle.

2

Aufgabe 1B

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_{a}$ mit

$f_{a}(x)=e^{x} \cdot(x-a)^{2}$ mit $a \in \mathbb{R}$ .

Jeder Graph der Schar hat genau einen Hochpunkt und genau einen Tiefpunkt.

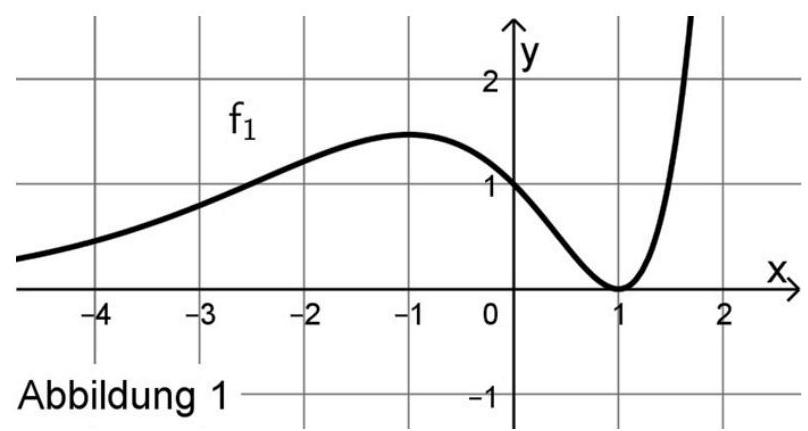
Der Graph von $f_{1}$ hat in einem seiner Wendepunkte eine negative Steigung.

Bestimmen Sie diesen Wendepunkt und diese Steigung. (6 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte

Berechnung der 1. und 2. Ableitung

Gegeben ist für $a=1$ : $f_{1}(x)=e^{x} \cdot(x-1)^{2}$ .

Berechne die 1. Ableitung mithilfe der Produktregel.

$f_1'(x)=e^x\cdot(x-1)^2+e^x\cdot 2\cdot(x-1)=e^x(x^2-2x+1+2x-2)$

$f_1'(x)=e^x\cdot(x^2-1)$

Entsprechend wird die zweite Ableitung berechnet:

$f_1''(x)=e^x\cdot(x^2-1)+e^x\cdot 2x=e^x\cdot(x^2-1+2x)=e^x\cdot(x^2+2x-1)$

Setze $f''(x)=0$

Die notwendige Bedingung für einen Wendepunkt ist $f''(x)=0$ .

Es muss also $e^x\cdot(x^2+2x-1)=0$ sein. Da $e^x$ immer ungleich null ist, wird die Klammer gleich null gesetzt und mit der pq-Formel gelöst.

$\Rightarrow\; x^2+2x-1=0$

Es ist $p=2$ und $q=-1$ :

$\displaystyle x_{1{,}2}$	$=$	$\displaystyle -\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}$
	↓	Setze $p=2$ und $q=-1$ ein.
	$=$	$\displaystyle -\frac{2}{2}\pm\sqrt{\left(\frac{2}{2}\right)^2-(-1)}$
	$=$	$\displaystyle -1\pm\sqrt{2}$

Man erhält die beiden Lösungen:

$x_1=-1-\sqrt{2}\approx-2{,}4$ und $x_2=-1+\sqrt{2}\approx0{,}4$

Gefordert war in der Aufgabenstellung ein Wendepunkt mit negativer Steigung.

Betrachtet man den Graphen von $f$ , dann ist an der Stelle $x_2=0{,}4$ die Steigung des Graphens negativ. Somit befindet sich der gesuchte Wendepunkt an der Stelle $x_2$ .

Berechne noch $f_1(-1+\sqrt{2})$ , um die Koordinaten des Wendepunktes angeben zu können:

$\displaystyle f_1(-1+\sqrt{2})$	$=$	$\displaystyle e^{(-1+\sqrt{2})}\cdot(-1+\sqrt{2}-1)^2$
	↓	Fasse zusammen.
	$=$	$\displaystyle e^{(-1+\sqrt{2})}\cdot(\sqrt{2}-2)^2$
	$≈$	$\displaystyle 0{,}5$

Somit hat der gesuchte Wendepunkt die Koordinaten: $WP\left(-1+\sqrt{2}|f_1(-1+\sqrt{2})\right) \;\Rightarrow\;WP(0{,}4|0{,}5)$

Bestimmung der Steigung in diesem Wendepunkt

Es ist $f_1'(x)=e^x\cdot(x^2-1)$ .

Setze $x_2=-1+\sqrt{2}$ ein:

$f_1'(-1+\sqrt{2})=e^{(-1+\sqrt{2})}\cdot\left((-1+\sqrt{2})^2-1\right)\approx-1{,}3$

Die Steigung in diesem Wendepunkt beträgt rund $-1{,}3$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Jeder Graph von $f_{a}$ hat mit jeder der beiden Koordinatenachsen genau einen gemeinsamen Punkt.
Geben Sie die Koordinaten dieser Punkte an.
Begründen Sie, dass der gemeinsame Punkt mit der $x$ -Achse der Tiefpunkt des Graphen von $f_{a}$ ist. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkte mit den beiden Koordinatenachsen
Für den Schnittpunkt mit der y-Achse berechne $f_a(0)$ :
$f_a(0)=e^0(0-a)^2=a^2\;\Rightarrow\;S_y(0|a^2)$
Für den Schnittpunkt mit der x-Achse berechne $f_a(x)=0$ :
$0=e^{x} \cdot(x-a)^{2}$
Da $e^x$ immer ungleich null ist, muss $(x-a)^2=0$ sein. $\;\Rightarrow\;x_{1{,}2}=a$
$\Rightarrow\;N_{1{,}2}(a|0)$
Begründung, dass der gemeinsame Punkt mit der x-Achse der Tiefpunkt des Graphen von f ist
Für die Funktion $f_a(x)$ gilt, dass sie für alle $x$ größer oder gleich null ist.
Der Punkt $(a|0)$ muss demnach der Tiefpunkt sein.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für den Schnittpunkt mit der y-Achse berechne $f_a(0)$ .
Für den Schnittpunkt mit der x-Achse (Nullstelle) berechne $f_a(x)=0$ .
Beachte, dass $f_a(x)$ für alle $x$ größer oder gleich null ist. Was bedeutet das für die gefundene Nullstelle?

Für jeden Wert von $a$ mit $a \neq 0$ schließt die Gerade durch die beiden Extrempunkte des Graphen von $f_{a}$ mit den Koordinatenachsen ein Dreieck ein.

Berechnen Sie denjenigen Wert von $a$ , für den dieses Dreieck gleichschenklig ist. (6 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichschenkliges Dreieck

Bestimmung der Extrempunkte

Es ist $f_a'(x)=e^x\cdot(x-a)\cdot(2+x-a)$ .

$e^x\cdot(x-a)\cdot(2+x-a)=0$

Da $e^x$ immer ungleich null ist, muss eine der Klammern gleich null sein (Satz vom Nullprodukt).

Die erste Nullstelle ist $x=a$ , mit dem Tiefpunkt $TP(a|0)$ (siehe Aufgabe b).

Die zweite Nullstelle ist bei $2+x-a=0$ , d.h. $x=a-2$ .

An dieser Stelle muss der Hochpunkt vorliegen.

$f_a(a-2)=e^{a-2}(a-2-a)^2=4\cdot e^{a-2}\;\Rightarrow\;HP(a-2|4\cdot e^{a-2})$

Geradengleichung

Gerade $y=m\cdot x+b$ durch die beiden Extrempunkte des Graphen von $f_{a}$ :

Es ist $m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{4\cdot e^{a-2}-0}{a-2-a}=-2\cdot e^{a-2}$

$\Rightarrow\;y=-2\cdot e^{a-2} \cdot x+b$

Setze den Punkt $(a|0)$ ein:

$0=-2\cdot e^{a-2} \cdot a+b\;\Rightarrow\;b=2\cdot a\cdot e^{a-2}$

$\Rightarrow\;y=-2\cdot e^{a-2} \cdot x+2\cdot a\cdot e^{a-2}$

Gleichschenkliges Dreieck

Diese Gerade schneidet die x-Achse bei $x=a$ und der y-Achsenabschnitt beträgt $2\cdot a\cdot e^{a-2}$ . Damit das Dreieck gleichschenklig ist, muss $a=2\cdot a\cdot e^{a-2}$ sein.

$\displaystyle a$	$=$	$\displaystyle 2\cdot a\cdot e^{a-2}$	$\displaystyle :a$
	↓	Da $a\neq 0$ kann durch $a$ geteilt werden.
$\displaystyle 1$	$=$	$\displaystyle 2\cdot e^{a-2}$	$\displaystyle :2$
$\displaystyle 0{,}5$	$=$	$\displaystyle e^{a-2}$	$\displaystyle \ln$
$\displaystyle \ln(0{,}5)$	$=$	$\displaystyle a-2$	$\displaystyle +2$
$\displaystyle \ln(0{,}5)+2$	$=$	$\displaystyle a$

Für $a=\ln(0{,}5)+2\approx1{,}307$ ist dieses Dreieck gleichschenklig.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Für jeden Wert von $a$ gilt: $f_{a}(a)=0$ und $f_{a}^{\prime}(a)=0$ und $f_{a}^{\prime \prime}(a) \neq 0$
Geben Sie die Bedeutung dieser Tatsache für die Graphen der Stammfunktionen zu $f_{a}$ an. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion, Integral und Flächenberechnung
Wenn $F_a(x)$ eine Stammfunktion von $f_a(x)$ ist, dann gilt nach Aufgabenstellung:
$F_a'(a) =f_a(a)=0\;\Rightarrow\;$ Die Stammfunktion hat an der Stelle $x=a$ eine waagrechte Tangente.
$F_a''(a) =f_a'(a)=0\;\Rightarrow\;$ An der Stelle $x=a$ hat der Graph der Stammfunktion einen Wendepunkt, da hier auch gilt, dass $F_a'''(a) =f_a''(a)\neq 0$ ist.
Somit hat der Graph der Stammfunktion $F_a(x)$ an der Stelle $x=a$ eine waagrechte Wendetangente. Es handelt sich hier um einen Terrassen- oder Sattelpunkt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es ist $F_a'(x) =f_a(x)$ , $F_a''(x) =f_a'(x)$ und $F_a'''(x) =f_a''(x)$ .
Untersuche, welche Werte die Ableitungen der Stammfunktion jeweils für $x=a$ annehmen und schließe dann auf mögliche besondere Punkte des Graphens der Stammfunktion.
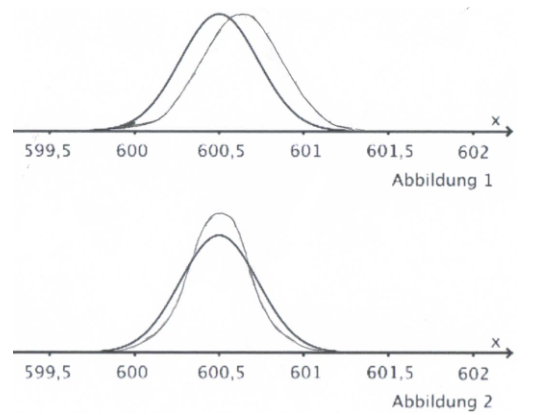
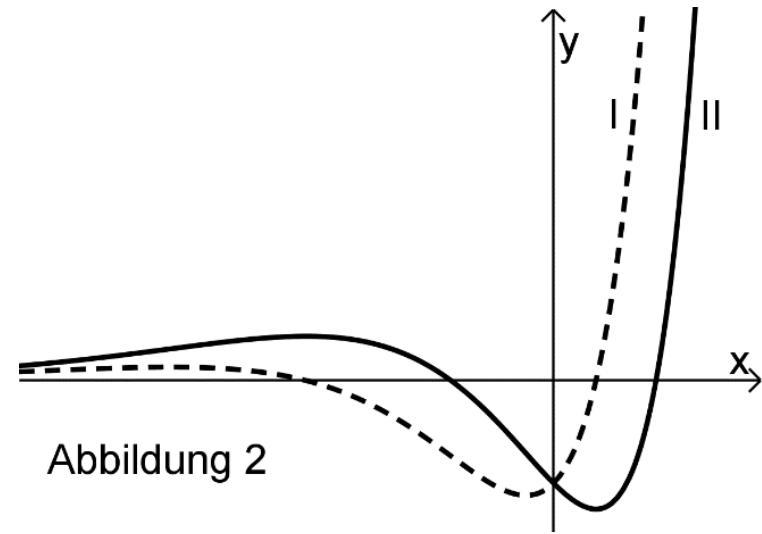
Abbildung 2 zeigt für einen bestimmten Wert von $a$ die Graphen von $f_{a}^{\prime}$ und $f_{a}^{\prime \prime}$ .
Entscheiden Sie, welcher der beiden Graphen I und II zu welcher Ableitungsfunktion gehört, und begründen Sie Ihre Entscheidung. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonie und Extrema
Der Graph I hat eine positive Nullstelle. Bei dieser positiven Nullstelle hat der Graph II ein Extremum (TP). Demnach muss der Graph 1 zu $f''_a$ und der Graph II zu $f'_a$ gehören.
Der Graph II kommt als Ableitungsfunktion von Graph I nicht infrage, da an der Stelle, an der der Graph I einen Tiefpunkt hat, der Graph II keine Nullstelle hat.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Betrachte die positive Nullstelle von Graph I. An dieser Stelle hat Graph II einen Tiefpunkt.
Der Schalldruckpegel wird oft umgangssprachlich als Lautstärke bezeichnet. Bei einem bestimmten Weckton eines Weckers wird der Schalldruckpegel durch die Funktionen $h$ und $k$ beschrieben:
$h(x)=20 \cdot \sin (x)$ für $0 \leq x \leq 2$
$k(x)=20 \cdot \sin (x-2)+20 \cdot \sin (2)$
für $2 \leq x \leq 4$
Dabei ist $x$ die seit Beginn des Wecktons vergangene Zeit in Sekunden. $h(x)$ und $k(x)$ geben den Schalldruckpegel in Dezibel (db) an.
Die Abbildung 3 zeigt die Graphen von $h$ und $k$ .
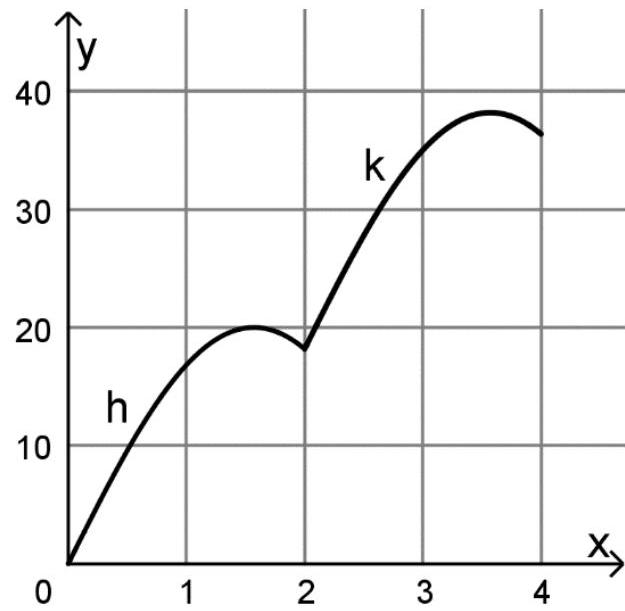
Abbildung 3
Berechnen Sie den Zeitpunkt, zu dem der Weckton den größten Schalldruckpegel hat.
(6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Der größte Schalldruckpegel wird im Verlauf der Funktion $k(x)$ erreicht.
Bestimmung des Maximums von $k(x)$
Berechne die 1. Ableitung und setze sie gleich null.
Es ist $k(x)=20 \cdot \sin (x-2)+20 \cdot \sin (2)\;\Rightarrow\;k'(x)=20 \cdot \cos (x-2)$ .
$k'(x)=0$
$\displaystyle 0$ $=$ $\displaystyle 20 \cdot \cos (x-2)$ $\displaystyle :20$
$\displaystyle 0$ $=$ $\displaystyle \cos (x-2)$
Der Kosinus hat eine Nullstelle bei $x=\dfrac{\pi}{2}\;$ .
$\Rightarrow\;x-2=\dfrac{\pi}{2}\;\Rightarrow\;x=2+\dfrac{\pi}{2}\approx3{,}57$
Nach etwa $3{,}6$ Sekunden wird der größte Schalldruckpegel erreicht.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der größte Schalldruckpegel wird im Verlauf der Funktion $k(x)$ erreicht.
Bestimme die Maximumstelle dieser Funktion.
Dem Graphen von $h$ ist zu entnehmen, dass der Weckton in den ersten zwei Sekunden bestimmte Schalldruckpegel mehr als einmal annimmt. Zwei Zeitpunkte mit gleichem Schalldruckpegel haben jeweils einen bestimmten Abstand.
Berechnen Sie den größten dieser Abstände. (6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
In der Abbildung sind für den Graphen von $h$ zwei Beispiele eingezeichnet, bei denen ein gleicher Schalldruckpegel vorliegt. Dabei wird deutlich, dass der Punkt $A$ zu diesem größten Abstand gehören muss.
Der Punkt $A$ hat die Koordinaten $A(2|20 \cdot \sin (2))$ . Gesucht sind nun die Koordinaten des Punktes $B$ , wobei $B$ den gleichen y-Wert wie der Punkt $A$ hat.
Die Differenz $x_A-x_B$ ist der gesuchte Abstand.
Bestimmung Punkt $B$
$B$ hat den gleichen y-Wert wie der Punkt $A$ $\;\Rightarrow\;$ $y=20 \cdot \sin (2)\approx18{,}1859$
Gesucht ist jetzt die x-Koordinate von $B \;\Rightarrow\;18{,}1859=20 \cdot \sin (x)$ .
$\Rightarrow\;\sin(x)=\dfrac{18{,}1859}{20}=0{,}9093$ oder $x=\sin^{-1}(0{,}9093)=1{,}1416$
Differenz $x_A-x_B$
Der größte Abstand hat dann die Länge:
$x_A-x_B=2-1{,}1416=0{,}8584\approx0{,}86\;\text{s}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Ein Punkt $A\in h$ hat die Koordinaten $A(2|20 \cdot \sin (2))$ .
Gesucht sind nun die Koordinaten des Punktes $B$ , wobei $B$ den gleichen $y$ -Wert wie der Punkt $A$ hat.
Die Differenz $x_A-x_B$ ist der gesuchte Abstand.
Berechnen Sie unter Verwendung der folgenden Information den durchschnittlichen Funktionswert von $k$ : (6 BE)
Der durchschnittliche Funktionswert von $k$ im Intervall $[a ; b]$ stimmt mit der Höhe eines Rechtecks überein, das die beiden folgenden Eigenschaften hat:
- Das Rechteck hat die Breite $b-a$ .
- Das Rechteck hat den gleichen Inhalt wie die Fläche, die für $a \leq x \leq b$ zwischen dem Graphen von $k$ und der $x$ -Achse liegt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Das Integral
Berechnung des Mittelwerts
Die Funktion $k$ ist im Intervall $[2;4]$ definiert.
Die Fläche eines Rechtecks $A$ ist Höhe $h$ mal Breite, wobei das Rechteck die Breite $4-2=2$ hat. $\;\Rightarrow\;A=h\cdot 2$
Weiterhin gilt:
Das Rechteck hat den gleichen Inhalt wie die Fläche, die für $2 \leq x \leq 4$ zwischen dem Graphen von $k$ und der $x$ -Achse liegt.
$\Rightarrow\;A= \displaystyle \int_2^4k(x) dx=\displaystyle \int_2^4\left(20 \cdot \sin (x-2)+20 \cdot \sin (2) \right)dx$
Das CAS liefert als Ergebnis: $A=64{,}6948\;\text{FE}$
$\Rightarrow\;64{,}6948=h\cdot 2$ bzw. $h\approx32{,}35$
Der durchschnittliche Funktionswert von $k$ entspricht der berechneten Höhe $32{,}35$ .
Alternative Berechnung des Mittelwertes
Für den Mittelwert gilt allgemein:
$\dfrac{1}{b-a}\cdot \displaystyle \int_a^bk(x) dx$
Mit den Grenzen $a=2$ und $b=4$ folgt dann:
$\dfrac{1}{4-2}\cdot \displaystyle \int_2^4k(x) dx=\dfrac{1}{2}\cdot 64{,}6948\approx 32{,}35$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die Funktion $k$ ist im Intervall $[2;4]$ definiert.
Die Fläche eines Rechtecks $A$ ist Höhe $h$ mal Breite, wobei das Rechteck die Breite $4-2=2$ hat.
Weiterhin ist $A= \displaystyle \int_2^4k(x) dx$ . Die beiden Flächeninhalte sind gleich groß.
Berechne durch Gleichsetzen der beiden Flächeninhalte die Höhe $h$ . Dies ist der gesuchte Mittelwert.

3

Aufgabe 1C

Die Abbildung 1 zeigt schematisch die achsensymmetrische Seitenansicht einer Brücke.

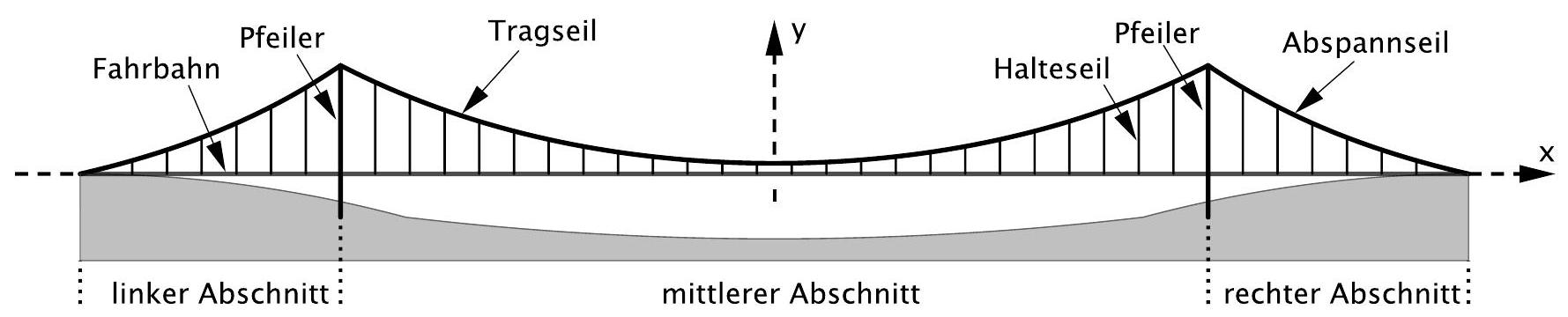
Die beiden vertikalen Pfeiler haben einen Abstand von $400 \mathrm{~m}$ . Am oberen Ende jedes Pfeilers ist sowohl das Tragseil des mittleren Abschnitts als auch das Abspannseil des linken bzw. rechten Abschnitts befestigt. Die beiden Abspannseile sind am jeweiligen Ende der Fahrbahn auf Fahrbahnhöhe verankert.

Im Koordinatensystem entspricht eine Längeneinheit $10 \mathrm{~m}$ in der Realität. In der Seitenansicht der Brücke verläuft die $x$ -Achse entlang der horizontal verlaufenden Fahrbahn, die $y$ -Achse entlang der Symmetrieachse.

Im rechten Abschnitt der Brücke wird der Verlauf des Abspannseils durch die Funktion $r$ mit $r(x)=2{,}53 \cdot\left(e^{\frac{1}{11} \cdot(32-x)}-1\right)$ beschrieben.

Zeigen Sie, dass die Fahrbahn der Brücke insgesamt $640 \mathrm{~m}$ lang ist. (4 BE)

Auch im linken Abschnitt der Brücke kann der Verlauf des Abspannseils durch einen Funktionsterm beschrieben werden.

Geben Sie einen passenden Term $l(x)$ sowie das Intervall an, in dem dieser Term das Abspannseil darstellt. (3 BE)

Berechnen Sie die Länge eines Pfeilers oberhalb der Fahrbahn. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Länge eines Pfeilers oberhalb der Fahrbahn.
Berechne $r(20)$ :
Definiere auf dem CAS die Funktion $r(x)$ und berechne dann $r(20)$ :
$r(20)\approx5{,}001757\approx5$
Mit der Längeneinheit $10 \mathrm{~m}$ in der Realität heißt das, der Pfeiler hat eine Länge von rund $50 \mathrm{~m}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $r(20)$ .
Beachte, dass die Längeneinheit $10 \mathrm{~m}$ in der Realität ist.
Berechnen Sie die Größe des Winkels, unter dem das rechte Abspannseil auf den rechten Pfeiler trifft. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung von Funktionen
Größe des Winkels, unter dem das rechte Abspannseil auf den rechten Pfeiler trifft
Berechne mit dem CAS die 1. Ableitung der Funktion $r(x)$ an der Stelle $x=20$ .
$r'(x)=2{,}53\cdot\left(-\dfrac{1}{11}\cdot\left(e^{\frac{1}{11} \cdot(32-x)}\right)\right)$
$r'(20)\approx-0{,}684705\;\Rightarrow\;\tan(\alpha)=-0{,}6847\;$
$\Rightarrow\;\alpha=\tan^{-1}(-0{,}6847)\approx-34{,}4^\circ$
Das ist der Winkel im 4. Quadranten. Der Winkel in dem eingezeichneten Dreieck (grün) (siehe Abbildung) ist dann $34{,}4^\circ$ und entsprechend der gesuchte Winkel (orange) ist dann $90^\circ -\alpha=90^\circ -34{,}4^\circ=55{,}6^\circ$ .
Skizze (wird nicht verlangt)
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die 1. Ableitung der Funktion $r(x)$ an der Stelle $x=20$ .
Setze $r'(20)=\tan(\alpha)$ . Dabei ist $\alpha$ der Winkel, den die Tangente mit der x-Achse einschließt. Gesucht ist aber der Winkel $90^\circ -\alpha$ .
In der Seitenansicht begrenzen der rechte Pfeiler, das Abspannseil und die Fahrbahn ein Flächenstück. Für eine Baumaßnahme wird zwischen Abspannseil und Fahrbahn eine Teilfläche des Flächenstücks mit einem Schutznetz verkleidet. Links wird die Teilfläche vom Pfeiler begrenzt und rechts endet sie mit einer vertikalen Begrenzung. Die Teilfläche soll halb so groß sein wie das gesamte Flächenstück.
Bestimmen Sie den Abstand der vertikalen Begrenzung zum Pfeiler. (6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Abstand der vertikalen Begrenzung zum Pfeiler.
Skizze
Berechne mit dem CAS zunächst die gesamte eingeschlossene Fläche:
$\displaystyle \int_{20}^{32}r(x)dx\approx24{,}65933\;\text{FE}$
Die Teilfläche soll halb so groß sein wie das gesamte Flächenstück:
$\displaystyle \int_{20}^{a}r(x)dx\approx \dfrac{24{,}65933}{2}\approx12{,}32967$
Löse mit dem CAS
Definiere $r(a)=\displaystyle \int_{20}^{a}r(x)dx$ und löse mit nSolve die obige Gleichung.
$\text{nSolve}(r(x)=12.32967,x,20)\;\Rightarrow\;x\approx23{,}04497$ bzw. das gesuchte $a$ .
Der gesuchte Abstand der vertikalen Begrenzung zum Pfeiler ist dann:
$23{,}045-20=3{,}045\;\text{LE}$ . Das sind rund $30{,}45\;\text{m}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne mit dem CAS zunächst die gesamte eingeschlossene Fläche.
Die Teilfläche soll halb so groß sein wie das gesamte Flächenstück. Das ergibt eine Gleichung, die mit nSolve gelöst wird.
Der gesuchte Abstand der vertikalen Begrenzung zum Pfeiler ist die Differenz der erhaltenen Lösung zu $20$ . (Beachte den Längenfaktor $10$ ).
Im Folgenden wird der mittlere Abschnitt betrachtet. Die 24 vertikal verlaufenden Halteseile verbinden die Fahrbahn mit dem Tragseil. Sie haben von den Pfeilern und untereinander einen horizontalen Abstand von jeweils $16 \mathrm{~m}$ . Der Verlauf des Tragseils wird durch die Funktion s mit $s(x)=\left(\frac{1}{8}\right)^{6} \cdot\left(x^{4}+2560 x^{2}\right)+\frac{125}{256}$ beschrieben.
Begründen Sie die Gültigkeit der folgenden Aussage: (2 BE)
Im Term von s ist erkennbar, dass die Seitenansicht der Brücke achsensymmetrisch ist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
Symmetrie des Graphen
Gegeben ist die Funktion $s(x)=\left(\frac{1}{8}\right)^{6} \cdot\left(x^{4}+2560 x^{2}\right)+\frac{125}{256}$ .
Die Funktion $s$ hat nur gerade Exponenten für die Variable $x$ .
Demnach ist die Funktion achsensymmetrisch zur y-Achse.
Alternativ kann gezeigt werden, dass $s(x)=s(-x)$ ist.
$s(-x)=\left(\frac{1}{8}\right)^{6} \cdot\left((-x)^{4}+2560 (-x)^{2}\right)+\frac{125}{256}=\left(\frac{1}{8}\right)^{6} \cdot\left(x^{4}+2560 x^{2}\right)+\frac{125}{256}=s(x)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Betrachte die Exponenten von $x$ .
Geben Sie die Bedeutung des Terms im Sachzusammenhang an:
$[s(-20+1{,}6 \cdot 1)+s(-20+1{,}6 \cdot 2)+\cdots+s(-20+1{,}6 \cdot 24)] \cdot 10$
Begründen Sie Ihre Angabe. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Bedeutung des Terms im Sachzusammenhang
Gegeben ist der Term:
$[s(-20+1{,}6 \cdot 1)+s(-20+1{,}6 \cdot 2)+\cdots+s(-20+1{,}6 \cdot 24)] \cdot 10$
Aus dem Aufgabentext entnimmt man:
"Die 24 vertikal verlaufenden Halteseile verbinden die Fahrbahn mit dem Tragseil. Sie haben von den Pfeilern und untereinander einen horizontalen Abstand von jeweils $16 \mathrm{~m}$ ."
Betrachte den ersten Term in der Klammer $s(-20+1{,}6 \cdot 1)$ .
Die Zahl 1,6 entspricht dem horizontalen Abstand der 24 vertikal verlaufenden Halteseile von jeweils $16 \mathrm{~m}$ .
In diesem ersten Term ist $x=-20+1{,}6=-18{,}4$ . Das ist die Stelle, an der sich auf der linken Seite neben dem linken Pfeiler das erste Halteseil unter dem Tragseil befindet.
$s(-20+1{,}6 \cdot 1)\cdot 10$ berechnet somit die Länge in Metern dieses ersten Halteseils.
Entsprechend werden die Längen aller 24 Halteseile berechnet und addiert.
Der Term $[s(-20+1{,}6 \cdot 1)+s(-20+1{,}6 \cdot 2)+\cdots+s(-20+1{,}6 \cdot 24)] \cdot 10$ gibt demnach die gesamte Länge der Halteseile im mittleren Brückenabschnitt in Metern an.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Überlege, was der Term $s(-20+1{,}6 \cdot 1)\cdot 10$ bedeutet.
Punkt $Q$ ist der Punkt auf dem rechten Pfeiler, der auf der Höhe der Fahrbahn liegt. Berechnen Sie den Abstand von $Q$ zum Tragseil. (7 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Abstand von Q zum Tragseil
Skizze
Der Punkt $Q$ hat die Koordinaten $Q(20|0)$ und der Punkt $P$ ist ein Punkt auf dem Tragseil $P(x|s(x))$ . Der Abstand von $Q$ zum Tragseil ist die Läge der Strecke $\overline{QP}$ .
Die Strecke $\overline{QP}$ muss für den kürzesten Abstand senkrecht auf $s$ stehen.
$\Rightarrow\;m_{\overline{QP}}=-\dfrac{1}{s'(x)}=\dfrac{s(x)-0}{x-20}$
Die Lösung dieser Gleichung erfolgt mit dem CAS.
Hier erfolgte die Lösung mit dem Geogebra-CAS:
GeoGebra-CAS
Die Rechnung mit dem Ti nspire CX CAS liefert das gleiche Ergebnis.
Damit kann nun der kürzeste Abstand mithilfe des Satzes von Pythagoras berechnet werden:
$|\overline{QP}|=\sqrt{(20-18{,}16)^2+s(18.16)^2}$
Die Lösung mit dem Geogebra-CAS:
GeoGebra-CAS
Der Abstand von $Q$ zum Tragseil beträgt rund $45{,}2\;\text{m}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Punkt $Q$ hat die Koordinaten $Q(20|0)$ und der Punkt $P$ ist ein Punkt auf dem Tragseil $P(x|s(x))$ . Der Abstand von $Q$ zum Tragseil ist die Länge der Strecke $\overline{QP}$ .
Die Strecke $\overline{QP}$ muss für den kürzesten Abstand senkrecht auf $s$ stehen, d.h. senkrecht auf der Tangente im Punkt $P$ an den Graphen von $s$ .
Dann gilt: $m_{\overline{QP}}=-\dfrac{1}{s'(x)}$
Überlege Dir, wie $m_{\overline{QP}}$ außerdem mithilfe eines Steigungsdreiecks bestimmt werden kann. Die beiden Steigungen sind gleich groß.
Die daraus sich ergebende Gleichung wird mit dem CAS gelöst.
Mit dem Satz des Pythagoras erfolgt die Berechnung des Abstandes.
Die Punkte $A(-20 \mid s(-20)), C(0 \mid s(0))$ und $B(20 \mid s(20))$ werden in dieser Reihenfolge durch Strecken verbunden.
Berechnen Sie die Summe der Streckenlängen und begründen Sie, dass die Länge des Tragseils größer ist als die Summe der Streckenlängen in der Realität. (6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
Summe der Streckenlängen
Skizze
Die gesamte Streckenlänge $L$ ist:
$L=2\cdot |\overline{BC}|=2\cdot \sqrt{(20-0)^2+(s(20)-s(0))^2}$
(Faktor 2 wegen der Symmetrie)
Geogebra-CAS
Mit der Längeneinheit $10 \mathrm{~m}$ in der Realität heißt das, die Streckenlänge $L$ beträgt rund $410{,}1 \mathrm{~m}$ .
Begründung, dass die Länge des Tragseils größer ist als die Summe der Streckenlängen in der Realität
Eine Gerade ist immer der kürzeste Abstand zwischen zwei Punkten.
Das Tragseil zwischen zwei Punkten hängt in der Realität immer etwas durch, d.h. es verläuft entlang einer Kurve. Deshalb muss die Tragseillänge größer als die Länge der beiden Geraden sein.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die gesamte Streckenlänge $L$ ist gleich $2\cdot |\overline{BC}|$ .
$|\overline{BC}|$ berechnet du mit dem Satz des Pythagoras und dem Einsatz des CAS.
Beachte im zweiten Teil der Aufgabe, dass das Tragseil durchhängt.

4

Aufgabe 2A

Die Sektoren des abgebildeten Glücksrads sind gleich groß und mit den Zahlen von 0 bis 9 beschriftet.

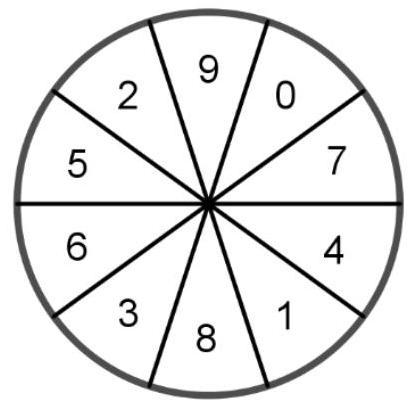
Das Glücksrad wird zwanzigmal gedreht.
Bestimmen Sie die Wahrscheinlichkeiten der Ereignisse $A$ und $B$ . (5 BE)
$A$ : „Es wird genau siebenmal eine ungerade Zahl erzielt.“
$B$ : „Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt.“
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Es ist $n=20$ .
A: "Es wird genau siebenmal eine ungerade Zahl erzielt".
Unter den zehn Zahlen auf dem Glücksrad gibt es insgesamt fünf ungerade Zahlen:
$\{1, 3, 5, 7, 9\}$
$\Rightarrow\;p(\text{ungerade})=\dfrac{5}{10}=\dfrac{1}{2}$
Gesucht ist $P_{20;0{,}5}(X=7)=B(20;\frac{1}{2};7)$
$\text{binompdf}(20;\frac{1}{2};7)\approx0{,}0739$
Die Wahrscheinlichkeit, dass genau siebenmal eine ungerade Zahl erzielt wird, beträgt $0{,}0739$ oder rund $7{,}4\;\%$ .
B: "Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt".
Gesucht ist $P_{20;0{,}5}(7<X\leq 12)$ :
$\text{binomcdf}(20;0{,}5;8;12)\approx0{,}7368$
Die Wahrscheinlichkeit, dass mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt wird, beträgt $0{,}7368$ oder rund $74\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
A: Berechne $P_{20;0{,}5}(X=7)$ mithilfe der Binomialverteilung.
B: Berechne $P_{20;0{,}5}(7<X\leq 12)$ mithilfe der Verteilungsfunktion.
Das Glücksrad wird zweimal gedreht.
Untersuchen Sie, ob die Ereignisse $C$ und $D$ stochastisch unabhängig sind. (5 BE)
$C$ : „Die Summe der erzielten Zahlen ist kleiner als $4 .{ }^{\prime \prime}$
$D$ : „Das Produkt der erzielten Zahlen ist 2 oder 3.“
Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastisch unabhängig
Betrachte zunächst die Ereignisse $C$ und $D$ .
C: "Die Summe der erzielten Zahlen ist kleiner als $4$ ".
Möglich sind hier die Ereignisse $C=\{00, 01, 10, 02, 20, 03, 30, 11, 12, 21\}$ .
Das sind $10$ von $100$ möglichen Ereignissen $\;\Rightarrow\;P(C)=\dfrac{10}{100}=\dfrac{1}{10}$ .
D: "Das Produkt der erzielten Zahlen ist $2$ oder $3$ ".
Möglich sind hier die Ereignisse $D=\{12, 21, 13, 31 \}$ .
Das sind $4$ von $100$ möglichen Ereignissen $\;\Rightarrow\;P(D)=\dfrac{4}{100}=\dfrac{1}{25}$ .
Ereignisse $C$ und $D$ stochastisch unabhängig
Bei stochastischer Unabhängigkeit gilt:
Die Schnittmenge der beiden Ereignisse $C$ und $D$ ist:
$C\cap D=\{12{,}21\}$
Das sind $2$ von $100$ möglichen Ereignissen $\;\Rightarrow\;P(C\cap D)=\dfrac{2}{100}=0{,}02$ .
Andererseits ist $P(C)=\dfrac{1}{10}$ und $P(D)=\dfrac{4}{100}$ .
$\Rightarrow\;P(C)\cdot P(D)=\dfrac{1}{10} \cdot\dfrac{4}{100}=\dfrac{4}{1000}=0{,}004$
$P(C\cap D)\neq P(C)\cdot P(D)$ denn $0{,}02 \neq 0{,}004$
Die Ereignisse $C$ und $D$ sind nicht stochastisch unabhängig.
Sie sind stochastisch abhängig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Stelle fest, welche Ereignisse zu $C$ bzw. zu $D$ gehören und berechne $P(C)$ und $P(D)$ .
Bei stochastischer Unabhängigkeit gilt: $P(C\cap D)=P(C)\cdot P(D)$
Bestimme $P(C\cap D)$ und vergleiche mit dem Produkt von $P(C)$ und $P(D)$ .

Mit dem Glücksrad wird ein Spiel durchgeführt. Jeder Spieler darf das Glücksrad beliebig oft drehen. Beendet er das Spiel selbst, bevor er eine „0“ erzielt, so wird ihm die Summe der erzielten Zahlen in Euro ausgezahlt. Erzielt er eine „ 0 “, so ist das Spiel dadurch beendet und es erfolgt keine Auszahlung.

Bei einem Spieler beträgt nach mehrmaligem Drehen des Glücksrads die Summe der erzielten Zahlen 60. Er dreht das Glücksrad genau ein weiteres Mal.

Berechnen Sie den Erwartungswert für den ausgezahlten Betrag. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert

Auszahlungsbeträge und Wahrscheinlichkeiten

Die Werte der Zufallsgröße $X$ sind die Auszahlungsbeträge in $€$ .

Die Summe der erzielten Zahlen beträgt $60$ .

Er spielt noch einmal und erzielt mit einer Wahrscheinlichkeit von $0{,}1$ eine "0". Dann beträgt die Auszahlung $0\;€$ (erste Spalte).

Er spielt noch einmal und erzielt mit einer Wahrscheinlichkeit von $0{,}1$ eine "1". Dann beträgt die Auszahlung $60+1=61\;€$ (zweite Spalte).

$.......$

Er spielt noch einmal und erzielt mit einer Wahrscheinlichkeit von $0{,}1$ eine "9". Dann beträgt die Auszahlung $60+9=69\;€$ (letzte Spalte).

$x_i$	0	61	62	63	64	65	66	67	68	69
$P(X=x_i)$ $~~~~~~~~~~~~~~~~~~~$	$0{,}1$	$0{,}1$	$0{,}1$	$0{,}1$	$0{,}1$	$0{,}1$	$0{,}1$	$0{,}1$	$0{,}1$	$0{,}1$

Erwartungswert

Für den Erwartungswert gilt dann:

$\def\arraystretch{1.25} \displaystyle \begin{array}{c c l}\text E (\text X) & = & x_1\cdot\text P (\text X =x_1) +x_2\cdot\text P (\text X =x_2) +\cdots+x_n\cdot\text P (\text X =x_n) \\ & = & \sum\limits_{i=1}^{n}x_i\cdot\text P (\text X = x_i)\end{array}$ $E(X)=(0+61+62+63+64+65+66+67+68+69)\cdot 0{,}1=58{,}5\;€$

Der Erwartungswert beträgt $58{,}5\;€$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Der Spieler dreht das Glücksrad bis er eine „ 0 “ erzielt, aber höchstens $n$ -mal. Der Erwartungswert für die Auszahlung beträgt in diesem Fall $5 n \cdot 0{,}9^{n}$ .

Beurteilen Sie die folgende Aussage: (4 BE)

Es gibt zwei, aber nicht drei aufeinanderfolgende Werte von n, für die die Erwartungswerte für die Auszahlung übereinstimmen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert

Erwartungswert

Der Erwartungswert für die Auszahlung ist $E(X)=5n\cdot 0{,}9^n$ .

Es gibt zwei, aber nicht drei aufeinanderfolgende Werte von $n$ , für die die Erwartungswerte für die Auszahlung übereinstimmen.

Zwei aufeinanderfolgende Werte für $n$ sind $n$ und $n+1$ . Also sollen die Terme $5n\cdot 0{,}9^n$ und $5(n+1)\cdot 0{,}9^{n+1}$ übereinstimmen.

Ansatz: $5n\cdot 0{,}9^n=5(n+1)\cdot 0{,}9^{n+1}$

Bestimmung der Werte

$\displaystyle 5n\cdot0{,}9^n$	$=$	$\displaystyle 5(n+1)\cdot 0{,}9^{n+1}$	$\displaystyle :5$
	↓	Löse nach $n$ auf. Teile durch $5$ .
$\displaystyle n\cdot0{,}9^n$	$=$	$\displaystyle (n+1)\cdot 0{,}9^{n+1}$	$\displaystyle :0{,}9^n$
	↓	Teile durch $0{,}9^n$ .
$\displaystyle n$	$=$	$\displaystyle (n+1)\cdot 0{,}9$
	↓	Löse die Klammer auf.
$\displaystyle n$	$=$	$\displaystyle 0{,}9n+0{,}9$	$\displaystyle -0{,}9n$
$\displaystyle 0{,}1n$	$=$	$\displaystyle 0{,}9$	$\displaystyle :0{,}1$
$\displaystyle n$	$=$	$\displaystyle 9$

Für $n=9$ und $n=10$ sollen die Erwartungswerte übereinstimmen.

Überprüfung:

$n=9\;\Rightarrow\;E(X)=5\cdot 9\cdot 0{,}9^9=45\cdot 0{,}9^9$

$n=10\;\Rightarrow\;E(X)=5\cdot 10\cdot 0{,}9^{10}=50\cdot 0{,}9\cdot 0{,}9^9=45\cdot 0{,}9^9$

Also stimmen die Erwartungswerte für $n=9$ und $n=10$ überein.

Es gibt zwei, aber nicht drei aufeinanderfolgende Werte von $n$

Die obige Gleichung für $n$ hat nur eine einzige Lösung, nämlich $n=9$ . Demnach kann es nur zwei und nicht drei aufeinanderfolgende Werte von $n$ geben. Hätte die obige Gleichung hingegen zwei verschiedene Lösungen für $n$ , dann gäbe es drei aufeinanderfolgende Werte von $n$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Betrachtet wird nun ein Glücksrad mit 10 nicht gleich großen Sektoren. Die Sektoren sind mit den Zahlen von 0 bis 9 beschriftet.
Bei 80 Drehungen wird zwölfmal die „0“ erzielt. Auf dieser Grundlage wird zur Sicherheitswahrscheinlichkeit $95 \%$ ein Konfidenzintervall für die Wahrscheinlichkeit, bei einer Drehung die "0“ zu erzielen, bestimmt.
Begründen Sie, dass die obere Grenze des Konfidenzintervalls größer als 0,1 ist. (4 BE)
Relative Häufigkeit
Bei $80$ Drehungen wird $12$ -mal die " $0$ " erzielt $\;\Rightarrow\;\dfrac{X}{n}=\dfrac{12}{80}=0{,}15$
Konfidenzintervall
Für ein $95 \%$ -Konfidenzintervall für die unbekannte Wahrscheinlichkeit $p$ , bei einer Drehung die " $0$ “ zu erzielen gilt:
$\left|\dfrac{X}{n}-p\right|\leq1{,}96\cdot\dfrac{\sigma}{n}\;\Rightarrow\;\left|0{,}15-p\right|\leq1{,}96\cdot\dfrac{\sigma}{n}$
Demnach liegt die Wahrscheinlichkeit $p$ im Intervall:
$0{,}15-1{,}96\cdot\dfrac{\sigma}{n}\leq p\leq0{,}15+1{,}96\cdot\dfrac{\sigma}{n}$ .
Die rechte Grenze des Intervalls ist immer größer als $1{,}5$ und ist damit auch größer als $0{,}1$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bei $80$ Drehungen wird $12$ -mal die " $0$ " erzielt $\;\Rightarrow\;\dfrac{X}{n}=\dfrac{12}{80}=0{,}15$
Für ein $95 \%$ -Konfidenzintervall für die unbekannte Wahrscheinlichkeit $p$ , bei einer Drehung die " $0$ “ zu erzielen gilt: $\left|0{,}15-p\right|\leq1{,}96\cdot\dfrac{\sigma}{n}$
Demnach liegt die Wahrscheinlichkeit $p$ im Intervall: $0{,}15-1{,}96\cdot\dfrac{\sigma}{n}\leq p\leq0{,}15+1{,}96\cdot\dfrac{\sigma}{n}$
Vergleiche die rechte Intervallgrenze mit $0{,}1$ .

Bestimmen Sie die kleinste Anzahl an Drehungen, für die Folgendes gilt: (4 BE)

Wenn man bei genau $15 \%$ der Drehungen die „0" erzielt, dann steht dies bei einer Sicherheitswahrscheinlichkeit von $95 \%$ nicht in Einklang mit der Annahme, dass beim Drehen des Glücksrads die „0" mit einer Wahrscheinlichkeit von $10 \%$ erzielt wird.

5

Aufgabe 2B

Für ein Land wird die Gruppe derjenigen Personen betrachtet, die im Jahr 2022 eine Urlaubsreise unternahmen.

Aus der betrachteten Gruppe wird eine Person zufällig ausgewählt. Untersucht werden die folgenden Ereignisse:

$W$ : „Die Person ist weiblich.“

$Z$ : „Die Person war mit ihrer Urlaubsreise zufrieden.“

Das nebenstehende Baumdiagramm veranschaulicht die Situation.

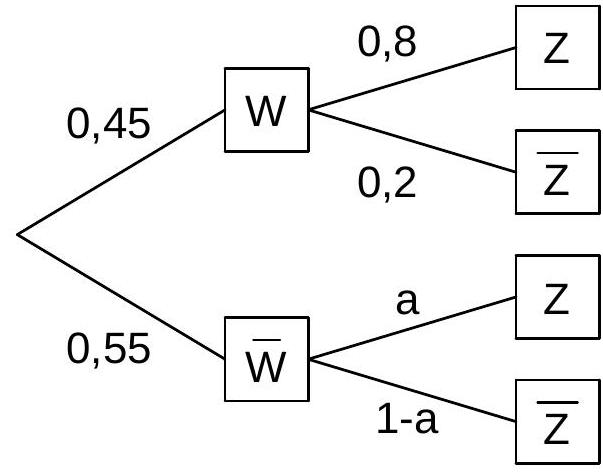
Die Wahrscheinlichkeit dafür, dass eine ausgewählte Person mit ihrer Urlaubsreise zufrieden war, beträgt $77{,}8 \%$ .

Bestimmen Sie den zugehörigen Wert von $a$ . (3 BE)

Weisen Sie nach, dass es in der betrachteten Gruppe für $a=0{,}7$ weniger weibliche als nicht weibliche Personen geben würde, die mit ihrer Urlaubsreise zufrieden waren.
(2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Vergleiche im Baumdiagramm die entsprechenden Pfade, die zu $Z$ führen
$P(W\cap Z)=0{,}45 \cdot 0{,}8=0{,}36$ und $P(\overline{W}\cap Z)=0{,}55 \cdot a.$
Für $a=0{,}7$ folgt dann $P(\overline{W}\cap Z)=0{,}55 \cdot 0{,}7=0{,}385$ .
Demnach ist $P(W\cap Z)=0{,}36 < P(\overline{W}\cap Z)=0{,}385$ .
Für $a=0{,}7$ gibt somit weniger weibliche als nicht weibliche Personen, die mit ihrer Urlaubsreise zufrieden waren.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Vergleiche im Baumdiagramm die entsprechenden Pfade, die zu $Z$ führen.
Geben Sie denjenigen Wert von $a$ an, für den $W$ und $Z$ stochastisch unabhängig sind. Begründen Sie Ihre Angabe, ohne zu rechnen. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Wert für $a$ bei stochastischer Unabhängigkeit
Bei stochastischer Unabhängigkeit der beiden Größe $W$ und $Z$ muss $P_W(Z)$ gleich $P_{\overline{W}}( Z)$ sein, d.h. die Zufriedenheit ist unabhängig vom Geschlecht.
Aus der Aufgabenstellung folgt $P_W(Z)=0{,}8$ und $P_{\overline{W}}( Z)=a$ .
Aus der Gleichheit folgt $a=0{,}8$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bei stochastischer Unabhängigkeit der beiden Größe $W$ und $Z$ muss $P_W(Z)$ gleich $P_{\overline{W}}( Z)$ sein.
Die ausgewählte Person war mit ihrer Urlaubsreise nicht zufrieden.
Begründen Sie im Sachzusammenhang, dass die Wahrscheinlichkeit dafür, dass die Person weiblich ist, mit zunehmendem Wert von $a$ zunimmt. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Untersuchen der Wahrscheinlichkeit
Betrachte $P({W}\cap \overline{Z})=0{,}45\cdot 0{,}2=0{,}09$ und $P(\overline{W}\cap \overline{Z})=0{,}55\cdot (1-a).$
Wird der Wert von $a$ größer, dann wird $P(\overline{W}\cap \overline{Z})$ kleiner, d.h. der Anteil nicht weiblicher Teilnehmer wird kleiner.
Da aber der die Gesamtzahl der Unzufriedenen gleich bleibt, muss die Anzahl der unzufriedenen weiblichen Teilnehmer zunehmen.
Begründung
Sehr deutlich wird das für $a=1$ , dann ist $P(\overline{W}\cap \overline{Z})=0$ und es gibt nur noch unter allen Unzufriedenen weibliche Teilnehmer.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Vergleiche die beiden Wahrscheinlichkeiten $P({W}\cap \overline{Z})$ und $P(\overline{W}\cap \overline{Z}).$
Wie ändert sich $P(\overline{W}\cap \overline{Z})$ , wenn $a$ größer wird und welche Auswirkung hat das auf $P({W}\cap \overline{Z})$ ?

Ein Reiseunternehmen führt ein Gewinnspiel durch. Jede Person kann nur einmal an dem Spiel teilnehmen. Als Ergebnis des Spiels wird eine bestimmte Anzahl von Strandkörben angezeigt. Diese Anzahl beträgt 0,1,2 oder 3. Im Folgenden sind die möglichen Gewinne beschrieben:

Wird kein Strandkorb angezeigt, so gewinnt die Person nichts.
Werden 1, 2 oder 3 Strandkörbe angezeigt, so gewinnt die Person einen Gutschein.

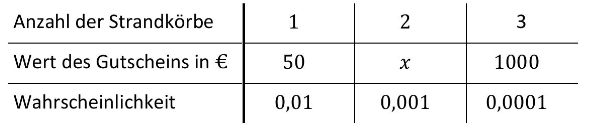
Bei dem Spiel beträgt der Erwartungswert des Gewinns pro Person 80 Cent.

Berechnen Sie die Wahrscheinlichkeit dafür, dass bei dem Spiel kein Strandkorb angezeigt wird.

Bestimmen Sie für die Personen mit zwei Strandkörben den Wert des Gutscheins.

(4 BE)

80000 Personen nehmen an dem Spiel teil. Die Zufallsgröße $Y$ beschreibt die Anzahl der Personen mit zwei Strandkörben. Der Erwartungswert der Zufallsgröße $Y$ wird mit $\mu_{Y}$ bezeichnet.
Ermitteln Sie den kleinsten möglichen ganzzahligen Wert von $c$ , für den die Anzahl der Personen mit zwei Strandkörben mit einer Wahrscheinlichkeit von mindestens $80 \%$ im Intervall $\left[\mu_{Y}-c ; \mu_{Y}+c\right]$ liegt. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zufallsgröße
Wert der Wahrscheinlichkeit
Es ist $n=80000$ und $p=0{,}001$ . Dann ist $\mu_Y=n\cdot p=80000\cdot 0{,}001=80$ .
Gesucht ist die Wahrscheinlichkeit $P_{80000;0{,}001}(80-c\leq X\leq 80+c)\geq 0{,}8.$
Löse die Gleichung mit $\text{binomCdf}$ .
Definiere $\text{bf(x)}=\text{binomCdf}(80000{,}0.001{,}80-x,80+x)$ und löse die Gleichung mit $\text{nSolve}$ : $\text{nSolve}\left( bf(x)=0.8,x,0{,}80\right)=11$
Die Probe $\text{bf(11)}=0{,}8021459$ zeigt, dass für $c=11$ die Wahrscheinlichkeit
$P_{80000;0{,}001}(80-11\leq X\leq 80+11)=0{,}8021459> 0{,}8$ ist.
Der kleinst mögliche ganzzahlige Wert von $c$ ist $11$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne den Erwartungswert $\mu_Y$ für $n=80000$ und $p=0{,}001$ .
Löse dann die Gleichung $P_{80000;0{,}001}(80-c\leq X\leq 80+c)\geq 0{,}8$ .

In der ersten Woche haben 1200 Personen an dem Spiel teilgenommen. Von diesen haben 7 Personen einen Gutschein gewonnen.

Beurteilen Sie auf Grundlage einer Sicherheitswahrscheinlichkeit von $99 \%$ , ob die Wahrscheinlichkeit für den Gewinn eines Gutscheins mit dem Ergebnis verträglich ist. (5 BE)

Wahrscheinlichkeit für den Gewinn eines Gutscheins

$p=0{,}01+0{,}001+0{,}0001=0{,}0111$ .

Es ist $n=1200$ und $X=7$ .

Konfidenzintervall

Für ein $99 \%$ -Konfidenzintervall für die unbekannte Wahrscheinlichkeit $p$ für den Gewinn eines Gutscheins gilt:

$\left|\dfrac{X}{n}-p\right|\leq2{,}58\cdot\dfrac{\sigma}{n}\;\Rightarrow\;\left|\dfrac{7}{1200}-p\right|\leq2{,}58\cdot\dfrac{\sigma}{1200}$

Demnach liegt die Wahrscheinlichkeit $p$ im Intervall:

$\dfrac{7}{1200}- 2{,}58\cdot\dfrac{\sigma}{1200}\leq p\leq\dfrac{7}{1200}+ 2{,}58\cdot\dfrac{\sigma}{1200}$

Aus dieser Ungleichung folgt:

$p-\dfrac{7}{1200}\leq2{,}58\cdot\dfrac{\sigma}{1200}=2{,}58\cdot\sqrt{\dfrac{p\cdot(1-p)}{1200}}$

Damit folgt:

$\displaystyle p-\dfrac{7}{1200}$	$≤$	$\displaystyle 2{,}58\cdot\sqrt{\dfrac{p\cdot(1-p)}{1200}}$	$\displaystyle ()^2$
$\displaystyle \left(p-\dfrac{7}{1200}\right)^2$	$≤$	$\displaystyle 2{,}58^2\cdot\dfrac{p\cdot(1-p)}{1200}$

Die Randwerte der quadratischen Ungleichung für $p$ werden mithilfe des CAS bestimmt.

$\text{nSolve}\left(\left(p-\dfrac{7}{1200}\right)^2=2{,}58^2\cdot\dfrac{p\cdot(1-p)}{1200},p,0\right)$

Man erhält die beiden Werte $p_1=0{,}0022806$ und $p_2=0{,}0148381$ .

Die Ungleichung ist für $p=0{,}0111$ erfüllt, da $0{,}0022806\leq 0{,}0111\leq0{,}0148381$ eine wahre Aussage ist. Die Wahrscheinlichkeit für den Gewinn eines Gutscheins ist mit dem Ergebnis verträglich.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

6

Aufgabe 2C

Ein Unternehmen stellt Olivenöl her und füllt es in Flaschen ab. Laut Aufdruck beträgt die Füllmenge jeder Flasche $600 \mathrm{ml}$ .

Für jede Flasche beträgt die Wahrscheinlichkeit dafür, dass sie weniger als $600 \mathrm{ml}$ Öl enthält, $1{,}5\%$ . Die Anzahl der Flaschen mit weniger als $600 \mathrm{ml}$ Öl wird durch eine Binomialverteilung beschrieben. Die Flaschen werden in Kartons verpackt. Jeder Karton enthält zwölf Flaschen.

Bestimmen Sie die Wahrscheinlichkeit dafür, dass in einem Karton weniger als zwei Flaschen mit weniger als $600 \mathrm{ml}$ Öl enthalten sind. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Weniger als zwei Flaschen mit weniger als $600\; \mathrm{ml}$ Öl enthalten
$X$ : Anzahl der Flaschen, die weniger als $600 \mathrm{ml}$ Öl enthalten.
Jeder Karton enthält zwölf Flaschen $\;\Rightarrow\;n=12.$
Für jede Flasche beträgt die Wahrscheinlichkeit dafür, dass sie weniger als $600 \mathrm{ml}$ Öl enthält, $1{,}5\%$ $\;\Rightarrow\;p=0{,}015.$
Berechne: $P(X<2)=P(X\leq 1)=\text{binomCdf}(12{,}0.015{,}0,1)\approx0{,}99$
Die Wahrscheinlichkeit dafür, dass in einem Karton weniger als zwei Flaschen mit weniger als $600 \mathrm{ml}$ Öl enthalten sind, beträgt rund $99\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $P(X<2)$ mit $n=12$ und $p=0{,}015$ .
Die Wahrscheinlichkeit ist binomialverteilt.

An einen Supermarkt wird regelmäßig die gleiche Anzahl von Flaschen geliefert. Dabei enthalten im Mittel mehr als 780 Flaschen mindestens $600 \mathrm{ml}$ Öl. Ermitteln Sie, wie viele Flaschen mindestens geliefert werden. (4 BE)

Ein Karton gilt als fehlerhaft, wenn mehr als eine Flasche weniger als $600 \mathrm{ml}$ Öl enthält.
Ein Supermarkt erhält eine Lieferung von 150 Kartons.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass mehr als $3 \%$ der Kartons fehlerhaft sind. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Wahrscheinlichkeit, dass mehr als $3\;\%$ der Kartons fehlerhaft sind
$Y$ : Anzahl der fehlerhaften Kartons
$Y$ ist binomialverteilt mit $n=150$ und $p=P(X>1)$
$p=P(X>1)=\text{binomCdf}(12{,}0.015{,}2,12)\approx0{,}0134$
$3\;\%$ von $150$ Kartons sind $4{,}5\;\Rightarrow\;$ mehr als $3\;\%$ sind demnach 5 Kartons oder mehr, die fehlerhaft sind.
Berechne $P(Y\geq 5)=\text{binomCdf}(150{,}0.0134{,}5,150)\approx0{,}0523$
Die Wahrscheinlichkeit dafür, dass mehr als $3\;\%$ der Kartons fehlerhaft sind, beträgt rund $5\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$Y$ : Anzahl der fehlerhaften Kartons und $Y$ ist binomialverteilt mit $n=150$ und $p=P(X>1)$
Berechne $p$ .
Berechne $3\;\%$ von $150$ und überlege, was mehr als $3\;\%$ bedeutet.
Berechne $P(Y\geq 5)$ .
Die Füllmenge der Flaschen ist normalverteilt mit einem Erwartungswert von $600{,}5 \mathrm{ml}$ und einer Standardabweichung von $0{,}23 \mathrm{ml}$ .
Eine Flasche wird zufällig ausgewählt.
Ermitteln Sie für die folgenden Ereignisse jeweils die Wahrscheinlichkeit: (4 BE)
$A$ : „Die Flasche enthält mehr als $601 \mathrm{ml}$ Öl.“
$B$ : „Die Füllmenge der Flasche weicht höchstens um $0{,}5 \mathrm{ml}$ vom Erwartungswert ab.“
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
$A$ : „Die Flasche enthält mehr als $601 \mathrm{ml}$ Öl.“
$X$ : Füllmenge in $\mathrm{ml}$
Normalverteilung mit $\mu=600{,}5\; \mathrm{ml}$ und $\sigma=0{,}23\; \mathrm{ml}$
Gesucht ist:
Die Wahrscheinlichkeit, dass die Flasche mehr als $601\; \mathrm{ml}$ Öl enthält, beträgt rund $1{,}5\;\%$ .
$B$ : „Die Füllmenge der Flasche weicht höchstens um $0{,}5\; \mathrm{ml}$ vom Erwartungswert ab.“
Es ist $\mu-0{,}5=600$ und $\mu+0{,}5=601$
Berechne: $P(600\leq X\leq601)=\text{normCdf}(600, 601, 600.5, 0.23)\approx0{,}9702884$
Die Wahrscheinlichkeit, dass die Füllmenge der Flasche um höchstens $0{,}5\; \mathrm{ml}$ vom Erwartungswert abweicht, beträgt etwa $97\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
A: Berechne $P(X>601)=\text{normCdf}(601,\infty,600.5, 0.23)$ .
B: Berechne $P(600\leq X\leq601)=\text{normCdf}(600, 601, 600.5, 0.23)$ .
Das Unternehmen möchte die Wahrscheinlichkeit dafür, dass eine Flasche weniger als $600 \mathrm{ml}$ Öl enthält, verringern. Für die nötige Änderung der Maschine, die die Flaschen befüllt, gibt es zwei Vorschläge:
Vorschlag 1: Die eingestellte Füllmenge von 600,5 ml wird erhöht.
Vorschlag 2: Die Genauigkeit, mit der die eingestellte Füllmenge von 600,5 ml erreicht wird, wird erhöht.
Beide Abbildungen zeigen jeweils den Graphen der Dichtefunktion, die vor der Änderung der Maschine die Füllmenge der Flaschen beschreibt.
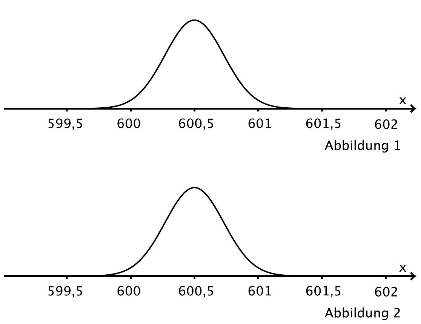
Skizzieren Sie in der Abbildung 1 den Graphen einer Dichtefunktion, die zu Vorschlag 1 passt und in der Abbildung 2 den Graphen einer Dichtefunktion, die zum Vorschlag 2 passt.
Begründen Sie für Vorschlag 1, dass damit das Ziel des Unternehmens erreicht wird.
(7 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Skizze des Graphen einer Dichtefunktion, die zu Vorschlag 1 passt und Dichtefunktion, die zum Vorschlag 2 passt
Skizzen
Vorschlag 1:
Der Erwartungswert der Verteilung muss größer werden, d.h. die Verteilung rutscht nach rechts. Die Form der Verteilung ändert sich nicht, d.h. die Genauigkeit der Abfüllung bleibt unverändert.
Vorschlag 2:
Hier muss der Erwartungswert beibehalten werden. Die Streuung um den Erwartungswert soll aber kleiner sein, d.h. der Graph wird etwas "schlanker". Dafür muss aber das Maximum größer werden, denn die Fläche unter dem Graphen muss weiterhin den Wert $1$ haben.
Begründung für Vorschlag 1, damit das Ziel des Unternehmens erreicht wird
Wie kann man am Graphen erkennen, wie wahrscheinlich es ist, dass die Flasche weniger als $600\; \mathrm{ml}$ Öl enthält?
Man findet diese Wahrscheinlichkeit als Fläche zwischen dem Graphen und der x-Achse im Intervall von minus unendlich bis $600$ .
Diese Fläche ist beim ursprünglichen Graphen größer als bei dem nach rechts verschobenen Graphen. In der Abbildung 1 ist die Fläche schwarz markiert, um die der ursprüngliche Graph in dem angegebenen Intervall größer ist.
Mit anderen Worten: Vorschlag 1 führt durch die Verschiebung in positive 𝑥-Richtung zu einer Verkleinerung dieser Fläche.
Der Vorschlag eignet sich dafür, dass die Firma ihr Ziel erreicht.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Vorschlag 1:
Der Erwartungswert der Verteilung muss größer werden, d.h. die Verteilung rutscht nach rechts. Die Form der Verteilung ändert sich nicht.
Vorschlag 2:
Der Erwartungswert wird beibehalten. Die Streuungs um den Erwartungswert soll aber kleiner sein, d.h. der Graph wird etwas "schlanker". Dafür muss aber das Maximum größer werden, denn die Fläche unter dem Graphen muss weiterhin den Wert $1$ haben.
Die Wahrscheinlichkeit, dass die Flasche weniger als $600\; \mathrm{ml}$ Öl enthält, entspricht der Fläche zwischen dem Graphen und der x-Achse in Intervall $]-\infty; 600]$ . Vorschlag 1 führt durch die Verschiebung in positive 𝑥-Richtung zu einer Verkleinerung dieser Fläche.
Bestimmen Sie die größtmögliche Standardabweichung mit einer Genauigkeit von drei Nachkommastellen, für die gilt: (4 BE)
Die Wahrscheinlichkeit dafür, dass eine Flasche weniger als $600 \mathrm{ml}$ Öl enthält, ist höchstens halb so groß.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Aufstellen der Ungleichung
Für $\mu = 600{,}5$ und $\sigma = 0{,}23$ gilt:
Aus Symmetriegründen ist $P(X>601)=0{,}015=P(X<600)$
$\Rightarrow\;P(X<600)=0{,}015$ und $0{,}5\cdot P(X<600)=0{,}0075$
Gesucht ist nun ein $\sigma$ , sodass $0{,}5\cdot P(X<600)\leq 0{,}0075$
Systematisches Probieren von $\sigma$
$\sigma=0{,}200\;\Rightarrow\;\text{normCdf}(-\infty, 600, 600.5, 0.20)\approx0{,}00621 <0{,}0075$
$\sigma=0{,}205\;\Rightarrow\;\text{normCdf}(-\infty, 600, 600.5, 0.205)\approx0{,}007363 <0{,}0075$
$\sigma=0{,}206\;\Rightarrow\;\text{normCdf}(-\infty, 600, 600.5, 0.206)\approx0{,}007608>0{,}0075$
Also ist die gesuchte Standardabweichung $\sigma=0{,}205$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Gesucht ist eine Standardabweichung $\sigma$ , sodass $0{,}5\cdot P(X<600)\leq 0{,}0075$ .
Probiere einige Werte für $\sigma$ aus.

7

Aufgabe 3A

Auf einem ebenen, horizontalen Gelände steht ein $15 \mathrm{~m}$ hoher Mast, an dem drei rechteckige Werbeflächen befestigt sind. In der Abbildung 1 ist eine der Werbeflächen grau dargestellt. Der Mast ist zylinderförmig und hat einen Durchmesser von $80 \mathrm{~cm}$ . Er verläuft ebenso wie die seitlichen Kanten der Werbeflächen vertikal.

In einem Koordinatensystem wird das Gelände durch die $x_1x_2$ -Ebene beschrieben. Eine Längeneinheit im Koordinatensystem entspricht $1$ m in der Wirklichkeit. Der Mittelpunkt der Grundfläche des Masts wird durch den Koordinatenursprung dargestellt. Die Punkte $A(5\mid-2\mid 11),B(-2\mid5\mid11),C,D(5\mid -2\mid 15),E(-2\mid 5\mid 15)$ und $F(-2\mid -2\mid 15)$ stellen Eckpunkte der Werbeflächen dar.

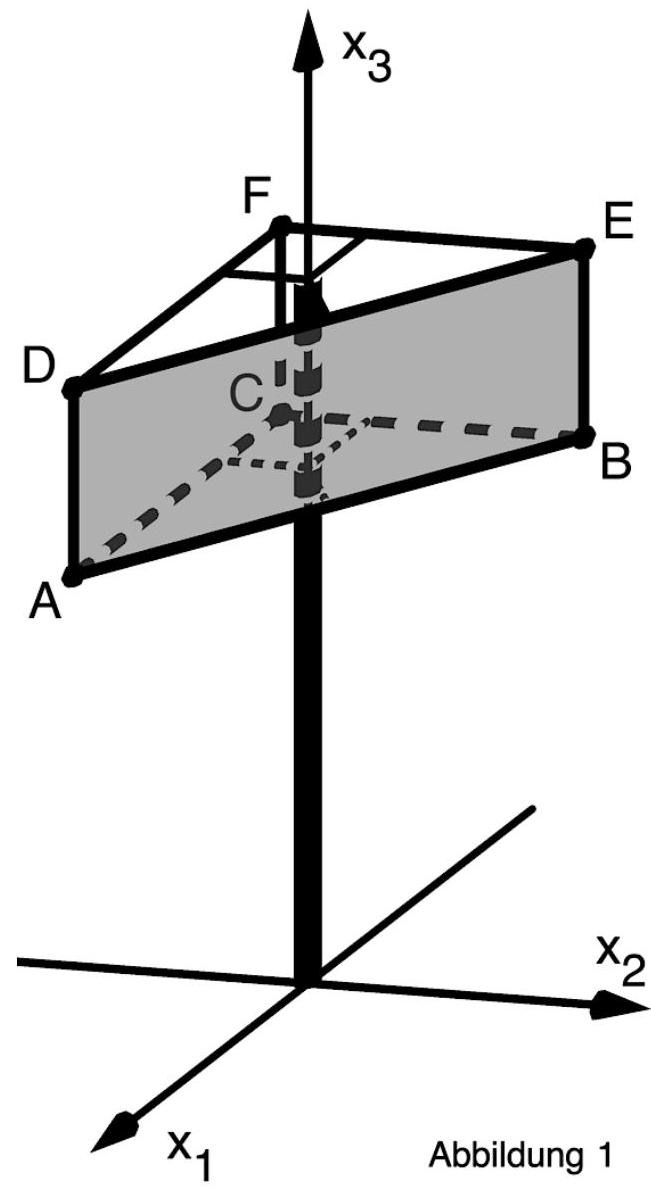
Bestimmen Sie den Flächeninhalt der grau dargestellten Werbefläche.
Untersuchen Sie, ob die beiden anderen Werbeflächen einen rechten Winkel einschließen. (6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
Flächeninhalt der grau dargestellten Werbefläche
Berechne die Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AD}$ .
$\overrightarrow{AB}=\begin{pmatrix}-2\\5\\11\end{pmatrix}-\begin{pmatrix}5\\-2\\11\end{pmatrix}=\begin{pmatrix}-7\\7\\0\end{pmatrix}$
$\overrightarrow{AD}=\begin{pmatrix}5\\-2\\15\end{pmatrix}-\begin{pmatrix}5\\-2\\11\end{pmatrix}=\begin{pmatrix}0\\0\\4\end{pmatrix}$
Senkrechte Vektoren
Prüfe, ob die beiden Vektoren senkrecht aufeinander stehen.
In diesem Fall handelt es sich um ein Rechteck.
Da das Skalarprodukt gleich null ist, stehen die beiden Vektoren senkrecht aufeinander.
$A_\square=\left|\overrightarrow{AB}\right| \cdot \left|\overrightarrow{AD}\right|=\sqrt{(-7)^2+7^2+0}\cdot \sqrt{0^2+0^2+4^2}=\sqrt{2\cdot49}\cdot 4=28\cdot \sqrt{2}$
$A_\square=28\cdot \sqrt{2}\approx39{,}6\;\text{m}^2$
Der Flächeninhalt der grau dargestellten Werbefläche beträgt etwa $39{,}6\;\text{m}^2$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AD}$ .
Prüfe, ob die beiden Vektoren senkrecht aufeinander stehen. In diesem Fall handelt es sich um ein Rechteck.
$A_\square=\left|\overrightarrow{AB}\right| \cdot \left|\overrightarrow{AD}\right|$
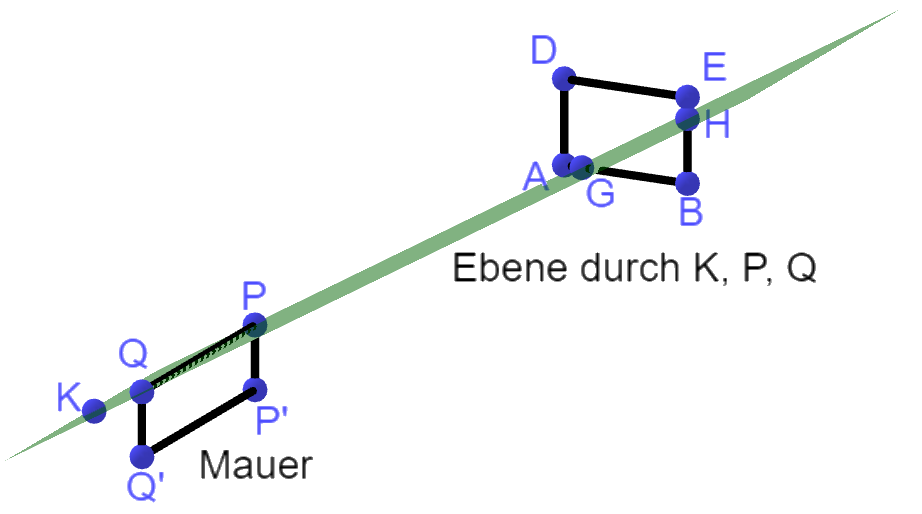
Die grau dargestellte Werbefläche liegt in einer Ebene, deren Gleichung in der Form $a \cdot x_{1}+a \cdot x_{2}=b$ dargestellt werden kann.
Ermitteln Sie passende Werte von $a$ und $b$ . (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebenengleichung aufstellen
Einsetzen der Koordinaten
Gegeben ist die Ebenengleichung $a \cdot x_{1}+a \cdot x_{2}=b$ .
Setze die Koordinaten des Punktes $A$ ein.
Demnach ist z.B. $a$ frei wählbar.
Setze $a=1$ , dann ist $b=3\cdot 1=3$
Passende Werte von a und b
Passende Werte von $a$ und $b$ sind $a=1$ und $b=3$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Gegeben ist die Ebenengleichung $a \cdot x_{1}+a \cdot x_{2}=b$ .
Setze die Koordinaten des Punktes $A$ ein. Du erhältst eine Gleichung für $a$ und $b$ .
Demnach ist z.B. $a$ frei wählbar, also z.B. $a=1$ . Dann kann auch $b$ angegeben werden.
Begründen Sie, dass der Abstand der grau dargestellten Werbefläche zum Mast mit dem Abstand des Mittelpunkts der oberen Kante dieser Werbefläche zum Mast übereinstimmt. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
Abstand der grau dargestellten Werbefläche zum Mast
Die Gleichung der grauen Ebene ist $E: \; x_1+x_2=3$ .
Die Ebene verläuft parallel zur $x_3$ -Achse. Der Mast verläuft entlang der $x_3$ -Achse (Symmetrieachse des Mastes).
Kein Punkt des Vierecks $ABCD$ hat einen kleineren Abstand zur $x_3$ -Achse als der Mittelpunkt $M$ der Strecke $\overline{DE}$ .
Die folgende Abbildung ist in der Aufgabenstellung nicht gefordert. Sie dient nur zur Veranschaulichung.
Skizze
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Betrachte die besondere Lage der Ebene $E$ .
Vergleiche mit der Lage des Mastes.
Beachte, um was für ein Dreieck es sich beim Dreieck $DEF$ handelt.
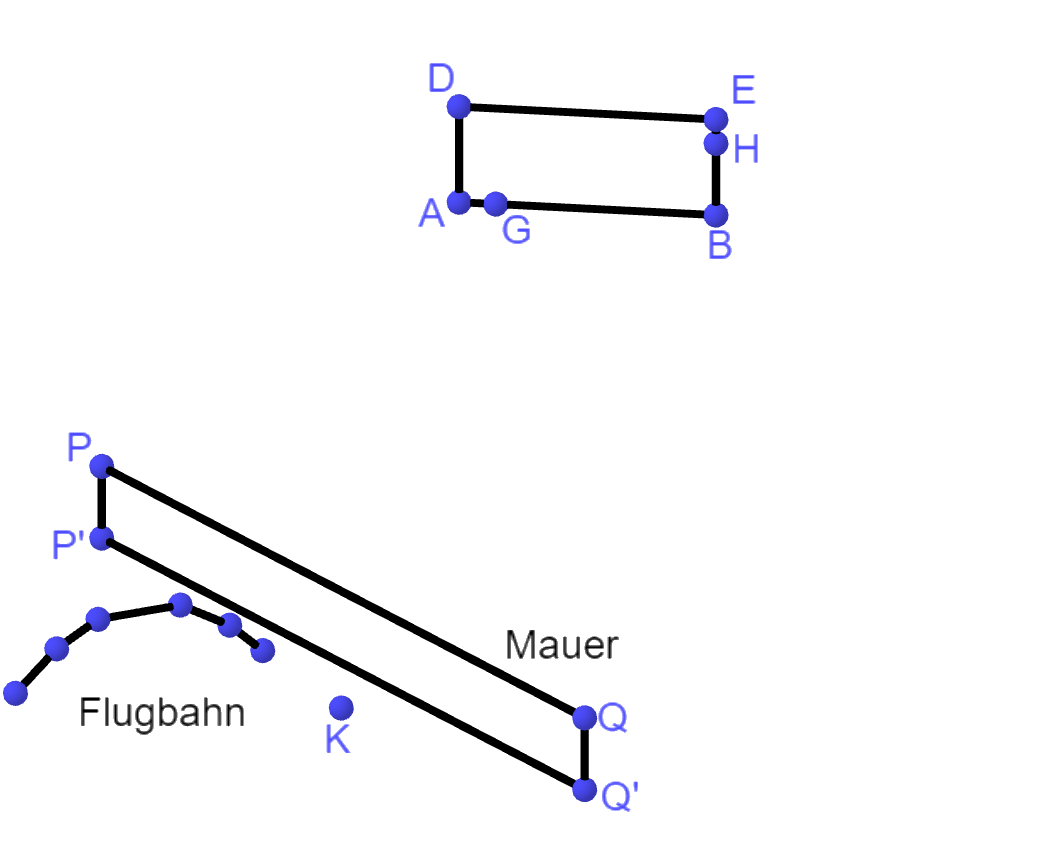
Auf dem Gelände befindet sich ein Sportplatz. Von dort aus blickt ein Kind zur grau dargestellten Werbefläche. Die Sicht des Kindes wird durch eine Mauer eingeschränkt. Die obere Kante der Mauer wird durch die Strecke zwischen den Punkten $P(20|-5| 3)$ und $Q(20|25| 3)$ dargestellt. Der Punkt, von dem der Blick des Kindes ausgeht, wird durch $K(24|15| 1)$ beschrieben. Das Kind kann denjenigen Teil der Werbefläche, der durch das Dreieck $G B H$ mit $G(4|-1| 11)$ dargestellt wird, nicht sehen (siehe Abbildung 2).
Eine Sichtlinie verläuft von $K$ zu $G$ .
Berechnen Sie die Größe des Winkels dieser Sichtlinie gegenüber dem horizontalen Gelände. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen Vektoren, Geraden und Ebenen
Größe des Winkels dieser Sichtlinie gegenüber dem horizontalen Gelände
Berechne den Vektor $\overrightarrow {KG}=\begin{pmatrix}4\\-1\\11\end{pmatrix}-\begin{pmatrix}24\\15\\1\end{pmatrix}=\begin{pmatrix}-20\\-16\\10\end{pmatrix}=2\cdot \begin{pmatrix}-10\\-8\\5\end{pmatrix}$ .
Der Normalenvektor der $x_1x_2$ -Ebene ist $\vec n=\begin{pmatrix}0\\0\\1\end{pmatrix}$ .
Dann gilt für den Winkel:
$\sin\alpha=\dfrac{\left|\begin{pmatrix}-10\\-8\\5\end{pmatrix}\circ\begin{pmatrix}0\\0\\1\end{pmatrix}\right|}{\sqrt{(-10)^2+(-8)^2+5^2}\cdot 1}=\dfrac{5}{\sqrt{189}}$
$\alpha=\sin^{-1}\left(\dfrac{5}{\sqrt{189}}\right)\approx21{,}3^\circ$
Die Größe des Winkels dieser Sichtlinie gegenüber dem horizontalen Gelände beträgt rund $21{,}3^\circ$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne den Vektor $\overrightarrow {KG}$ .
Der Normalenvektor der $x_1x_2$ -Ebene ist $\vec n=\begin{pmatrix}0\\0\\1\end{pmatrix}$ .
Dann gilt für den gesuchten Winkel: $\sin\alpha=\dfrac{\left|\overrightarrow {KG}\circ \vec n\right|}{\left|\overrightarrow {KG}\right|\cdot|\vec n|}$
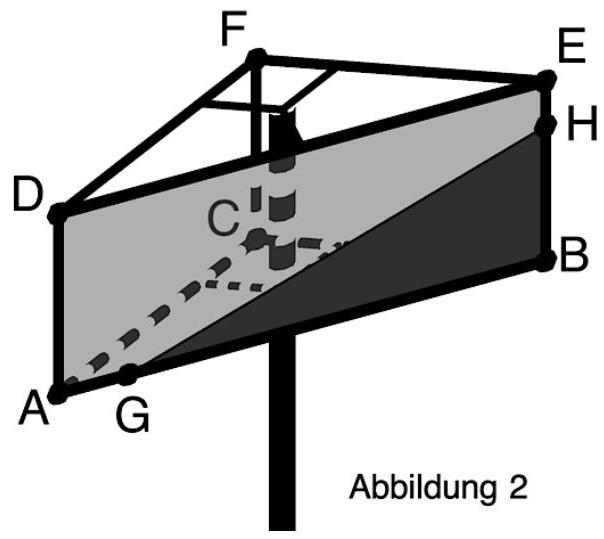
Berechnen Sie die Koordinaten von $H$ . (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene aus drei Punkten
Aufstellen der Ebene
Erstelle die Gleichung einer Ebene $E$ durch die drei Punkte $KPQ$ und schneide sie mit der Geraden $g$ , die durch die Punkte $B$ und $E$ verläuft.
$E_{KPQ}:\; \vec x=\overrightarrow {OK}+r\cdot \overrightarrow {KP}+s\cdot \overrightarrow {KQ}$
$E_{KPQ}:\; \vec x=\begin{pmatrix}24\\15\\1\end{pmatrix}+r\cdot \left(\begin{pmatrix}20\\-5\\3\end{pmatrix}-\begin{pmatrix}24\\15\\1\end{pmatrix}\right)+s\cdot \left(\begin{pmatrix}20\\25\\3\end{pmatrix}-\begin{pmatrix}24\\15\\1\end{pmatrix}\right)$
$E_{KPQ}:\; \vec x=\begin{pmatrix}24\\15\\1\end{pmatrix}+r\cdot \begin{pmatrix}-4\\-20\\2\end{pmatrix}+s\cdot \begin{pmatrix}-4\\10\\2\end{pmatrix}$
Gerade $g: \;\vec x=\overrightarrow {OB}+t\cdot\overrightarrow {BE}=\begin{pmatrix}-2\\5\\11\end{pmatrix}+t\cdot \left(\begin{pmatrix}-2\\5\\15\end{pmatrix}-\begin{pmatrix}-2\\5\\11\end{pmatrix}\right)$
$g: \;\vec x=\begin{pmatrix}-2\\5\\11\end{pmatrix}+t\cdot \begin{pmatrix}0\\0\\4\end{pmatrix}$
oder mit verkürztem Richtungsvektor
$g: \;\vec x==\begin{pmatrix}-2\\5\\11\end{pmatrix}+t\cdot \begin{pmatrix}0\\0\\1\end{pmatrix}$
Schnitt von Gerade und Ebene
Wir schneiden die Gerade und die Ebene: $g\cap E$
$\begin{pmatrix}24\\15\\1\end{pmatrix}+r\cdot \begin{pmatrix}-4\\-20\\2\end{pmatrix}+s\cdot \begin{pmatrix}-4\\10\\2\end{pmatrix}=\begin{pmatrix}-2\\5\\11\end{pmatrix}+t\cdot \begin{pmatrix}0\\0\\1\end{pmatrix}$
Der GTR-Rechner liefert die Lösung: $t=3$ .
Koordinaten von H
Setze $t=3$ in $g$ ein. Du erhältst die Koordinaten von $H$ .
$\overrightarrow {OH}=\begin{pmatrix}-2\\5\\11\end{pmatrix}+3\cdot \begin{pmatrix}0\\0\\1\end{pmatrix}=\begin{pmatrix}-2+0\\5+0\\11+3\end{pmatrix}=\begin{pmatrix}-2\\5\\14\end{pmatrix}\;\Rightarrow\;H(-2|5|14)$
Der Punkt $H$ hat die Koordinaten $H(-2|5|14)$ .
Anmerkung: Die folgende Abbildung ist nicht in der Aufgabe gefordert. Sie dient nur zur Veranschaulichung.
Skizze
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Erstelle die Gleichung einer Ebene $E$ durch die drei Punkte $KPQ$ .
Schneide die Ebene $E$ mit der Geraden $g$ , die durch die Punkte $B$ und $E$ verläuft.
Auf dem Sportplatz wird ein Fußball geschossen. Die Flugbahn des Balls wird durch Punkte der Form $\left(32-8 t|5|-5 t^{2}+6{,}5 t+0{,}3\right)$ mit $t \geq 0$ beschrieben. Dabei ist $t$ die seit dem Schuss vergangene Zeit in Sekunden.
Beschreiben Sie, wie man ermitteln könnte, ob der Ball die Mauer trifft, bevor er den Boden berührt. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor
Beschreibung wie man ermitteln könnte, ob der Ball die Mauer trifft
Jeder Punkt der Mauer hat die $x_1$ -Koordinate $20$ .
Die Flugbahn des Balls wird durch Punkte der Form $\left(32-8 t|5|-5 t^{2}+6{,}5 t+0{,}3\right)$ beschrieben.
Daraus ergibt sich die Gleichung: $32-8\cdot t=20\;\Rightarrow\;t_1$
Da die Mauer eine Höhe von $3$ Metern hat, kann der Ball die Mauer nur treffen, wenn gilt: $0<-5\cdot t_1^{2}+6{,}5\cdot t_1+0{,}3 \leq 3$ .
Anmerkung: Die folgende Abbildung ist nicht in der Aufgabe gefordert. Sie dient nur zur Veranschaulichung.
Skizze
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die $x_1$ -Koordinate der Mauer und die $x_1$ -Koordinate der Flugbahn ergeben eine Gleichung mit der Lösung $t_1$ .
Da die Mauer eine Höhe von $3$ Metern hat, kann der Ball die Mauer nur treffen, wenn die $x_3$ -Koordinate der Flugbahn zwischen $0$ und $3$ liegt.

8

Aufgabe 3B

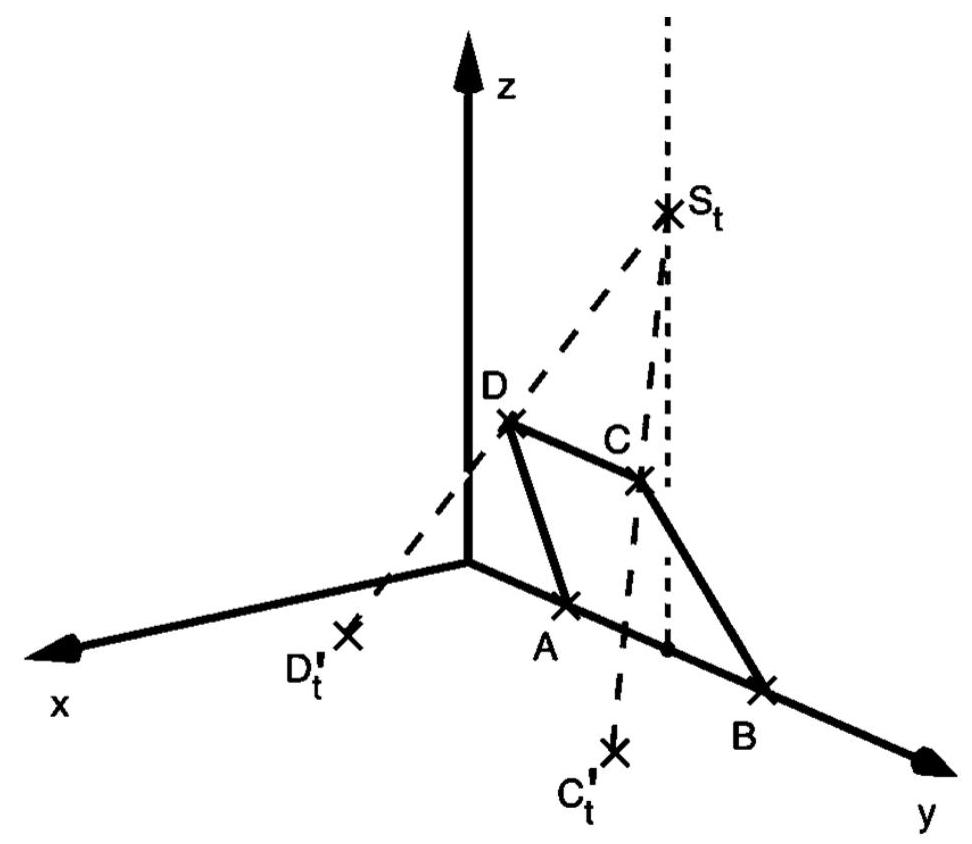
Die Abbildung 1 zeigt das Viereck $A B C D$ mit $A(0|3| 0), B(0|9| 0), C(2|8| 4)$ und $D(2|4| 4)$ . Gegeben sind außerdem die Punkte $S_{t}(0|6| t)$ mit $t \geq 0$ .

Weisen Sie nach,
- dass in dem Viereck $A B C D$ zwei Seiten parallel zueinander sind.
- dass in dem Viereck $A B C D$ zwei gegenüberliegende Seiten gleich lang sind.
- dass das Viereck $A B C D$ kein Rechteck ist.
(6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Viereck
Lösung
In dem Viereck ABCD sind zwei Seiten parallel zueinander
Gegeben sind $A(0|3| 0)$ , $B(0|9| 0)$ , $C(2|8| 4)$ und $D(2|4| 4)$ .
Bei den Punkten $A$ und $B$ und ebenso bei den Punkten $C$ und $D$ stimmen die
$x_1$ -Koordinaten und die $x_3$ -Koordinaten überein. Somit ist $\overline{AB}\parallel\overline{CD}$ .
In dem Viereck ABCD sind zwei gegenüberliegende Seiten gleich lang
Berechne die Vektoren $\overrightarrow{AD}$ und $\overrightarrow{BC}$ .
$\overrightarrow{AD}=\begin{pmatrix}2\\4\\4\end{pmatrix}-\begin{pmatrix}0\\3\\0\end{pmatrix}=\begin{pmatrix}2\\1\\4\end{pmatrix}$
$\overrightarrow{BC}=\begin{pmatrix}2\\8\\4\end{pmatrix}-\begin{pmatrix}0\\9\\0\end{pmatrix}=\begin{pmatrix}2\\-1\\4\end{pmatrix}$
Da bei beiden Vektoren die Koordinaten jeweils den gleichen Betrag haben, sind die Beträge der Vektoren gleich groß.
$\left|\overrightarrow{AD}\right|=\left|\overrightarrow{BC}\right|$
Das Viereck ABCD ist kein Rechteck
Berechne das Skalarprodukt zwischen den Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AD}$ . Prüfe damit, ob die beiden Vektoren senkrecht aufeinander stehen.
$\overrightarrow{AD}=\begin{pmatrix}2\\1\\4\end{pmatrix}$
$\overrightarrow{AB}=\begin{pmatrix}0\\9\\0\end{pmatrix}-\begin{pmatrix}0\\3\\0\end{pmatrix}=\begin{pmatrix}0\\6\\0\end{pmatrix}$
$\overrightarrow{AD}\circ\overrightarrow{AB}=\begin{pmatrix}2\\1\\4\end{pmatrix}\circ \begin{pmatrix}0\\6\\0\end{pmatrix}=2\cdot 0 +1\cdot 6 +4\cdot 0=6\neq 0$
Die beiden Vektoren stehen nicht senkrecht aufeinander, d.h. das Viereck $ABCD$ ist kein Rechteck.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
In dem Viereck $ABCD$ sind zwei Seiten parallel zueinander.
Betrachte bei den Punkten $A$ und $B$ und ebenso bei den Punkten $C$ und $D$ übereinstimmende Koordinaten.
In dem Viereck $ABCD$ sind zwei gegenüberliegende Seiten gleich lang.
Berechne die Vektoren $\overrightarrow{AD}$ und $\overrightarrow{BC}$ .
Das Viereck $ABCD$ ist kein Rechteck.
Prüfe mit dem Skalarprodukt, ob die beiden Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AD}$ senkrecht aufeinander stehen.
Bestimmen Sie eine Gleichung der Ebene $E$ , in der das Viereck $A B C D$ liegt, in Koordinatenform. (3 BE)
[Zur Kontrolle: $2 x-z=0$ ]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parameterform in Koordinatenform
Ebene in Parameterform
$E:\;\vec x=\overrightarrow{OA}+r\cdot \overrightarrow{AB}+s\cdot \overrightarrow{AD}=\begin{pmatrix}0\\3\\0\end{pmatrix}+r\cdot \begin{pmatrix}0\\6\\0\end{pmatrix}+s\cdot \begin{pmatrix}2\\1\\4\end{pmatrix}$
Umwandlung in Normalenform
Berechne den Normalenvektor $\vec n$ der Ebene $E$ :
$\vec n=\begin{pmatrix}0\\6\\0\end{pmatrix}\times \begin{pmatrix}2\\1\\4\end{pmatrix}=\begin{pmatrix}24\\0\\-12\end{pmatrix}=12\cdot \begin{pmatrix}2\\0\\-1\end{pmatrix}$
$E:\;\left(\vec x-\begin{pmatrix}0\\3\\0\end{pmatrix}\right)\circ\begin{pmatrix}2\\0\\-1\end{pmatrix}=0$
Berechne das Skalarprodukt:
$E:\; 2\cdot x+0\cdot y+(-1)\cdot z-(0+0+0)=0\;\Rightarrow\; 2\cdot x- z=0$
Das Viereck liegt in der Ebene $2\cdot x-z=0$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Erstelle eine Ebenengleichung in Parameterform und wandle sie in die Koordinatenform um.
Berechnen Sie den Winkel zwischen der $x y$ -Ebene und der Ebene $E$ , in der das Viereck $A B C D$ liegt. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen Vektoren, Geraden und Ebenen
Winkel zwischen der xy-Ebene und der Ebene E
Der Normalenvektor der xy-Ebene ist $\vec n_{xy}=\begin{pmatrix}0\\0\\1\end{pmatrix}$ und der Normalenvektor der Ebene $E$ ist $\vec n_{E}=\begin{pmatrix}2\\0\\-1\end{pmatrix}$ .
Dann folgt für den Winkel zwischen zwei Ebenen:
$\cos\alpha=\dfrac{|\vec n_{E}\circ \vec n_{xy}|}{|\vec n_{E}|\cdot |\vec n_{xy}}=\dfrac{\left|\begin{pmatrix}2\\0\\-1\end{pmatrix}\circ\begin{pmatrix}0\\0\\1\end{pmatrix}\right|}{\sqrt{2^2+0^2+(-1)^2}\cdot 1}=\dfrac{|-1|}{\sqrt{5}}$
$\alpha=\cos^{-1}\left(\dfrac{1}{\sqrt{5}}\right)\approx63{,}4^\circ$
Der Winkel zwischen der xy-Ebene und der Ebene $E$ beträgt rund $63{,}4^\circ$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Benutze die beiden Normalenvektoren der beiden Ebenen und berechne den Winkel mit $\cos\alpha=\dfrac{|\vec n_{E}\circ \vec n_{xy}|}{|\vec n_{E}|\cdot |\vec n_{xy}}$

Betrachtet werden die Geraden $g_{t}$ , die senkrecht zu der Ebene $E$ liegen und durch die Punkte $S_{t}$ verlaufen.

Ermitteln Sie diejenigen Werte von $t$ , für die der Schnittpunkt der zugehörigen Geraden $g_{t}$ und der Ebene $E$ im Inneren des Vierecks $A B C D$ liegt. (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen

Lösung

Geraden $g_{t}$ , die senkrecht zu der Ebene $E$ liegen und durch die Punkte $S_{t}$ verlaufen

Der Normalenvektor der Ebene $E$ ist $\vec n_{E}=\begin{pmatrix}2\\0\\-1\end{pmatrix}$ $\;\Rightarrow\;$ $g_t:\;\vec x=\overrightarrow{OS_{t}}+r \cdot \vec n_E=\begin{pmatrix}0\\6\\t\end{pmatrix}+r \cdot\begin{pmatrix}2\\0\\-1\end{pmatrix}$

Werte von $t$ , für die der Schnittpunkt der zugehörigen Geraden $g_t$ und der Ebene $E$ im Inneren des Vierecks $ABCD$ liegt

$g_t\cap E$ :

$\displaystyle 2\cdot(0+2r)-(t-r)$	$=$	$\displaystyle 0$
	↓	Löse die Klammer auf.
$\displaystyle 4r-t+r$	$=$	$\displaystyle 0$	$\displaystyle +t$
$\displaystyle 5r$	$=$	$\displaystyle t$	$\displaystyle :5$
$\displaystyle r$	$=$	$\displaystyle \frac{1}{5}t$

Eingesetzt in $g_t$ :

$\overrightarrow{OS_{t}}=\begin{pmatrix}0\\6\\t\end{pmatrix}+\frac{1}{5}t \cdot\begin{pmatrix}2\\0\\-1\end{pmatrix}=\begin{pmatrix}\frac{2}{5}t\\6\\t-\frac{1}{5}t\end{pmatrix}=\begin{pmatrix}\frac{2}{5}t\\6\\\frac{4}{5}t\end{pmatrix}$

$\Rightarrow\;S_t(\frac{2}{5}t|6|\frac{4}{5}t)$

Die x-Koordinate des Rechtecks läuft von $0$ bis $2$ .

Demnach muss für die x-Koordinaten der Schnittpunkte gelten:

$0<\frac{2}{5}t<2$ oder $0<t<5$ .

Gilt $0<t<5$ , dann liegt der Schnittpunkt der zugehörigen Geraden $g_t$ und der Ebene $E$ im Inneren des Vierecks $ABCD$ .

Anmerkung: Die folgende Abbildung ist in der Aufgabenstellung nicht gefordert. Die dient nur zur Veranschaulichung.

Dargestellt ist hier das Viereck $ABCD$ , die Ebene $E$ , der Punkt $S_5$ und die zu $E$ senkrechte Gerade $g_5$ .

Die obere Kante des Rechtecks wird von der Gerade $g_5$ in der Mitte geschnitten (Punkt $N$ ).

In diesem Fall liegt der Schnittpunkt der Geraden $g_5$ und der Ebene $E$ nicht im Inneren des Vierecks $ABCD$ . Erst, wenn $0<t<5$ ist, wird das Viereck im Innern geschnitten.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Im Folgenden gilt $t>4$ .
Die Gerade durch die Punkte $S_{t}$ und $C$ schneidet die $x y$ -Ebene im Punkt $C_{t}^{\prime}$ , die Gerade durch die Punkte $S_{t}$ und $D$ schneidet diese Ebene im Punkt $D_{t}^{\prime}$ (vgl. Abbildung 1).
Die beiden folgenden Gleichungen I und II liefern gemeinsam einen bestimmten Wert von $t$ .
I. $\overrightarrow{O S_{t}}+r \cdot \overrightarrow{S_{t} C}=\overrightarrow{O C_{t}^{\prime}}$ mit $C_{t}^{\prime}(x|y| 0)$
II. $\overrightarrow{B A} \cdot \overrightarrow{B C_{t}^{\prime}}=0$
Geben Sie für diesen Wert von $t$ die Art des Vierecks $A B C_{t}^{\prime} D_{t}^{\prime}$ an und begründen Sie Ihre Angabe. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Art des Vierecks $A B C_{t}^{\prime} D_{t}^{\prime}$
Es handelt sich um ein Rechteck.
Begründung
Aus Gleichung $\mathrm{II}\:\; \overrightarrow{B A} \cdot \overrightarrow{B C_{t}^{\prime}}=0$ folgt, dass die beiden Vektoren senkrecht aufeinander stehen.
Weiterhin ist das Viereck $ABCD$ symmetrisch zur Ebene $E_1:\; y=6$ .
Der Punkt $S_t$ liegt ebenfalls in der Ebene $E_1$ . Aus Symmetriegründen liegt der Punkt $D_t'$ symmetrisch zu $C_t'$ (bezüglich der Ebene $E_1$ ).
Ebenso liegt der Punkt $A$ symmetrisch zum Punkt $B$ . Dann steht auch $\overline{AD_t'}$ senkrecht zu $\overline{AB}$ und es ist $\overline{C_t'D_t'}$ parallel zu $\overline{AB}$ .
Die folgende Abbildung ist in der Aufgabenstellung nicht gefordert. Die dient nur zur Veranschaulichung.
Der eingezeichnete Winkel im Rechteck $A B C_{t}^{\prime} D_{t}^{\prime}$ ist ein rechter Winkel.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Betrachte Gleichung II. Was folgt aus dieser Gleichung?
Beachte, dass das Viereck $ABCD$ symmetrisch zur Ebene $E_1:\; y=6$ ist und dass der Punkt $S_t$ ebenfalls in der Ebene $E_1$ liegt.
Was folgt dann aus Symmetriegründen?
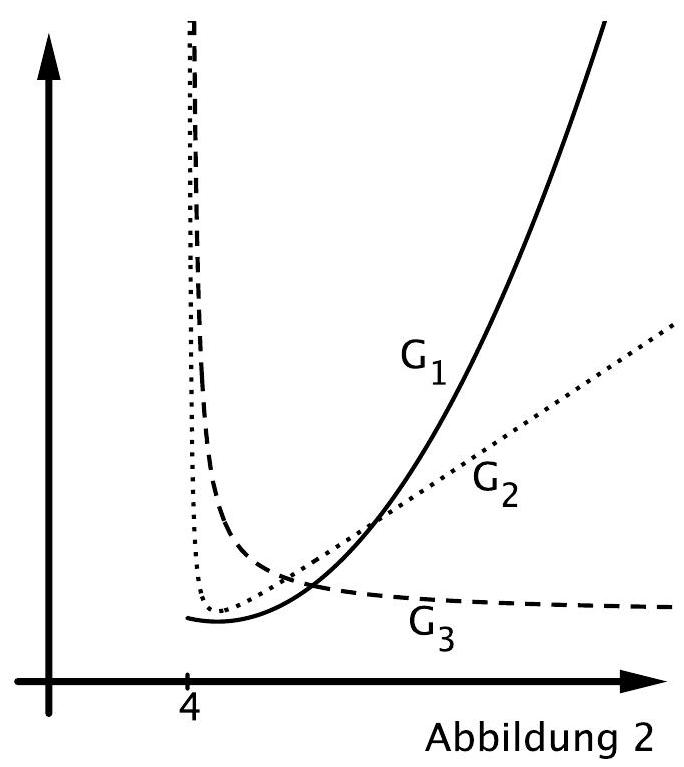
Das Volumen der Pyramide $A B C_{t}^{\prime} D_{t}^{\prime} S_{t}$ wird in Abhängigkeit von $t$ durch einen der drei abgebildeten Graphen $G_{1}, G_{2}$ und $G_{3}$ dargestellt (Abbildung 2).
Geben Sie diesen Graphen an und begründen Sie Ihre Angabe. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Richtiger Graph
Der Graph $G_2$ gehört zu dem Pyramidenvolumen $A B C_{t}^{\prime} D_{t}^{\prime} S_{t}$ in Abhängigkeit von $t$ .
Begründung
Das Pyramidenvolumen berechnet sich mit $V=\dfrac{1}{3}\cdot G\cdot h$ .
In diesem Fall ist das Pyramidenvolumen $V(t)=\dfrac{1}{3}\cdot G(t)\cdot t$ für $t>4$ .
Es besteht folgender Zusammenhang:
Nähert sich $t$ dem Wert $4$ , wird $G(t)$ beliebig groß, während die Höhe größer als $4$ ist. $\Rightarrow\; V\mapsto \infty$
Für $t\mapsto \infty$ wird die Höhe beliebig groß, während $G(t)$ immer kleiner wird und sich dem Flächeninhalt eines Rechtecks mit den Eckpunkten $A, B, (2|8|0)$ und $(2|4|0)$ nähert. $\Rightarrow\; V\mapsto \infty$
Es passt also nur Graph $G_2$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für das Pyramidenvolumen gilt $V(t)=\dfrac{1}{3}\cdot G(t)\cdot t$ für $t>4$ .
Untersuche, wie sich das Volumen verändert, wenn $t\mapsto 4$ geht bzw. wenn $t\mapsto \infty$ geht.
Schließe dann auf den passenden Graphen.

9

Aufgabe 3C

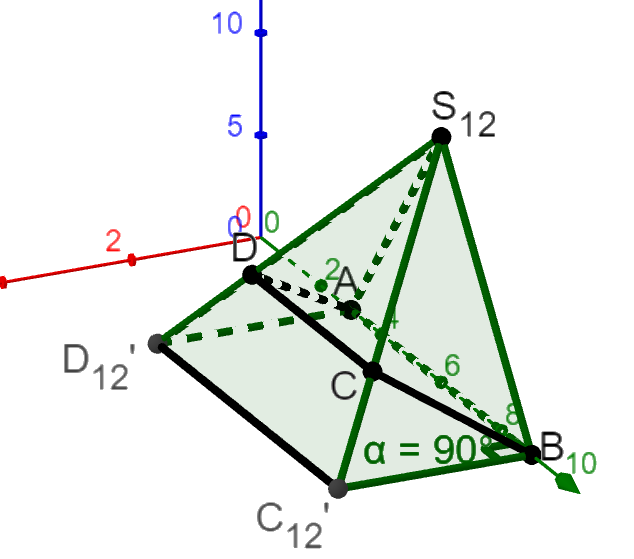
Die Abbildung 1 zeigt den Körper $A B C D E F$ mit $A(6|3| 0)$ , $\mathrm{B}(0|6| 0), C(3|0| 0), D(6|3| 6), E(0|6| 6)$ und $F(3|0| 12)$ .

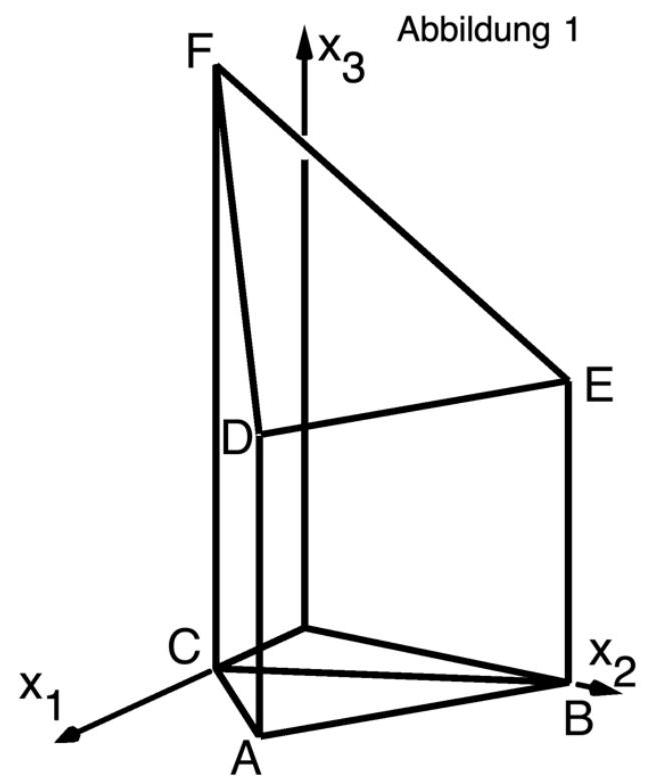
Die Punkte $D, E$ und $F$ liegen in der Ebene $L$ mit dem Normalenvektor $\def\arraystretch{1.25} \left(\begin{array}{l}2 \\ 4 \\ 3\end{array}\right)$ .

Geben Sie eine Gleichung von $L$ in Koordinatenform an.

Bestimmen Sie die Größe des Winkels, den $L$ mit der $x_{1} x_{2}$ -Ebene einschließt. (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene

Gleichung von $L$ in Koordinatenform

Erstelle zunächst die Ebenengleichung $L$ in Parameterform:

$L=E_{DEF}:\vec X=\vec{D}+r\cdot\overrightarrow{DE}+s\cdot\overrightarrow{DF}$

Berechne die Richtungsvektoren:

$\overrightarrow{DE}=\vec E-\vec D=\begin{pmatrix}0\\6\\6\end{pmatrix}-\begin{pmatrix}6\\3\\6\end{pmatrix}=\begin{pmatrix}-6\\3\\0\end{pmatrix}$

$\overrightarrow{DF}=\vec F-\vec D=\begin{pmatrix}3\\0\\12\end{pmatrix}-\begin{pmatrix}6\\3\\6\end{pmatrix}=\begin{pmatrix}-3\\-3\\6\end{pmatrix}$

Berechne den Normalenvektor der Ebene $L$ über das Kreuzprodukt der beiden Richtungsvektoren von $L$ .

$\vec n=\overrightarrow{DE}\times \overrightarrow{DF}$

$\vec n=\begin{pmatrix}-6\\3\\0\end{pmatrix}\times \begin{pmatrix} -3 \\-3 \\ 6 \end{pmatrix}=\begin{pmatrix} 18 \\36 \\ 27\end{pmatrix}=9\cdot \begin{pmatrix} 2 \\4\\ 3 \end{pmatrix}$

Benutze den verkürzten Normalenvektor $\vec n_L=\begin{pmatrix}2 \\4\\ 3 \end{pmatrix}$ .

Für die Normalenform gilt: $L: \;\left(\vec X-\vec D\right)\circ\vec n_L =0$

$\displaystyle \left(\vec{X}-\vec{D}\right)\circ\vec{n}_L$	$=$	$\displaystyle 0$
	↓	Setze $\vec D$ und $\vec n_L$ ein.
$\displaystyle \left(\vec X-\begin{pmatrix}6\\3\\6\end{pmatrix}\right)\circ\begin{pmatrix}2\\4\\3\end{pmatrix}$	$=$	$\displaystyle 0$
$\displaystyle \left(\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}-\begin{pmatrix}6\\3\\6\end{pmatrix}\right)\circ\begin{pmatrix}2\\4\\3\end{pmatrix}$	$=$	$\displaystyle 0$
	↓	Wandle die Normalenform in die Koordinatenform um, indem das Skalarprodukt berechnet wird:
$\displaystyle x_1\cdot2+x_2\cdot4+x_3\cdot3-(6\cdot2+3\cdot4+6\cdot3)$	$=$	$\displaystyle 0$
	↓	Fasse zusammen
$\displaystyle x_1\cdot2+x_2\cdot4+x_3\cdot3-42$	$=$	$\displaystyle 0$

Die Gleichung der Ebene $L$ lautet: $x_1\cdot2+x_2\cdot4+x_3\cdot3-42=0$

Berechnung der Größe $\varphi$ des Winkels, den $L$ mit der $x_1x_2$ -Ebene einschließt

Der Normalenvektor der Ebene $L$ ist der Vektor $\vec n_L=\begin{pmatrix}2\\4\\3\end{pmatrix}$ .

Sein Betrag ist $|\vec n_L|=\sqrt{2^2+4^2+3^2}=\sqrt{29}$ .

Der Normalenvektor der $x_1x_2$ -Ebene ist $\vec n_{x_1x_2}=\begin{pmatrix}0\\0\\1\end{pmatrix}$ .

Sein Betrag ist $|\vec n_{x_1x_2}|=1$ .

Der Winkel zwischen den beiden Ebenen berechnet sich mit:

$\cos(\varphi)=\dfrac{\vec n_L\circ \vec n_{x_1x_2}}{|\vec n_L|\cdot |\vec n_{x_1x_2}|}$

$\displaystyle \cos(\varphi)$	$=$	$\displaystyle \dfrac{\vec n_L\circ \vec n_{x_1x_2}}{\|\vec n_L\|\cdot \|\vec n_{x_1x_2}\|}$
	↓	Setze die Vektoren und ihre Beträge ein.
	$=$	$\displaystyle \dfrac{\begin{pmatrix}2\\4\\3\end{pmatrix}\circ \begin{pmatrix}0\\0\\1\end{pmatrix}}{\sqrt{29}\cdot 1}$
	↓	Berechne das Skalarprodukt.
	$=$	$\displaystyle \dfrac{2\cdot0+4\cdot 0+3\cdot 1}{\sqrt{29}\cdot 1}$
	↓	Fasse zusammen.
	$=$	$\displaystyle \dfrac{3}{\sqrt{29}}$

Der Winkel $\varphi$ erhält man durch Anwendung der trigonometrischen Umkehrfunktion: $\varphi=\cos^{-1}\left(\dfrac{3}{\sqrt{29}}\right)\approx56{,}15^\circ$

Der Winkel, den $L$ mit der $x_1x_2$ -Ebene einschließt, beträgt rund $56{,}15^\circ$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

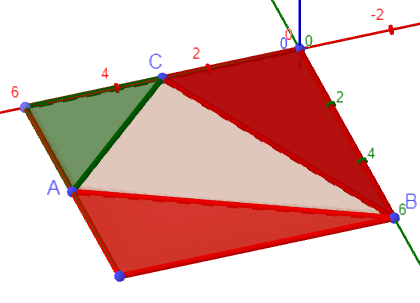
Der Flächeninhalt des Dreiecks $A B C$ kann mit dem Term
$6 \cdot 6-\frac{1}{2} \cdot 3 \cdot 3-2 \cdot \frac{1}{2} \cdot 3 \cdot 6$ berechnet werden
Veranschaulichen Sie diese Tatsache durch geeignete Eintragungen in der Abbildung 1. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreieck
Veranschaulichung des Terms $6\cdot 6-\dfrac{1}{2}\cdot 3\cdot 3 -2\cdot \dfrac{1}{2}\ 3\cdot 6$
Veranschaulichen Sie diese Tatsache durch geeignete Eintragungen in der Abbildung 1. In der folgenden Abbildung, die nur den Grundriss des Körpers zeigt, sind mehrere Flächen farbig markiert.
Skizze
Innerhalb eines Quadrates liegen vier Dreiecke. Warum ist es ein Quadrat?
Die Punkte A und B liegen auf diesem Quadrat. Der Punkt $A$ hat die $x_1$ -Koordinate $6$ und der Punkt $B$ hat die $x_2$ -Koordinate $6$ . $\Rightarrow\;A_\square=\textcolor{009999}{ 6\cdot 6 }$
Das ist der erste Term von $\textcolor{009999}{ 6\cdot 6 }-\textcolor{006400}{\dfrac{1}{2} \cdot 3\cdot 3 } -2\cdot \textcolor{cc0000}{\dfrac{1}{2} \cdot 3\cdot 6 }$ .
Der Punkt $A$ hat die $x_2$ -Koordinate $3$ und der Punkt $C$ hat die $x_1$ -Koordinate $3$ .
Die Fläche des $\textcolor{006400}{ \text{ grün} }$ gefärbten Dreiecks ist dann $A_\triangle=\textcolor{006400}{\dfrac{1}{2} \cdot 3\cdot 3 }$ .
Das ist der zweite Term von $\textcolor{009999}{ 6\cdot 6 }-\textcolor{006400}{\dfrac{1}{2} \cdot 3\cdot 3 } -2\cdot \textcolor{cc0000}{\dfrac{1}{2} \cdot 3\cdot 6 }$ .
Die beiden $\textcolor{cc0000}{ \text{rot} }$ gefärbten Dreiecke haben die Seitenlängen $3$ und $6$ und ihre Fläche ist jeweils $A_\triangle=\textcolor{cc0000}{\dfrac{1}{2} \cdot 3\cdot 6 }$ .
Diese beiden Dreiecksflächen ergeben zusammen den dritten Term in dem gegebenen Term.
Da vom Flächeninhalt der Quadratfläche insgesamt drei Flächeninhalte der Dreiecke subtrahiert werden, bleibt als Ergebnis der Flächeninhalt des $\textcolor{993300}{ \text{braunen} }$ Dreiecks $ABC$ übrig.
Der gegebene Term stellt also den Flächeninhalt des Dreiecks $ABC$ dar.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zeichne in die Abbildung ein Quadrat ein.
Der Punkt $A$ liegt auf einer Quadratseite. In dem Quadrat findet man das Dreieck $ABC$ und drei weitere Dreiecke.
Berechne den Flächeninhalt des Quadrates und subtrahiere die Flächeninhalte der drei um das Dreieck $ABC$ liegenden Dreiecke. Als Ergebnis erhältst Du den Flächeninhalt des Dreiecks $ABC$ .
Berechnen Sie das Volumen des Körpers $A B C D E F$ . (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Prisma
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Das Volumen des Körpers $ABCDEF$
Der Körper setzt sich aus zwei Teilen zusammen, ein dreiseitiges Prisma und eine dreiseitige Pyramide.
Volumen des dreiseitigen Prismas
$V_{\text{Prisma}}=G\cdot h$
Die Grundseite $G$ ist das Dreieck $ABC$ aus der Aufgabe b).
Der Flächeninhalt dieses Dreiecks ist:
Das Prisma hat die Höhe $h=6\;\text{LE}$ , da die $x_3$ -Koordinate des Punktes $D$ gleich $6$ ist.
Setze die Werte für $G$ und $h$ in die Volumenformel ein:
$\Rightarrow\;V_{\text{Prisma}}=13{,}5\cdot 6=81\;\text{VE}$
Volumen der dreiseitigen Pyramide
$V_{\text{Pyramide}}=\dfrac{1}{3}\cdot G\cdot h$
Die dreiseitige Pyramide hat die gleiche Grundfläche wie das Prisma
( $G=13{,}5\;\text{FE}$ ).
Die Höhe der Pyramide ist $h=12-6=6 \;\text{LE}$ , da die Differenz der $x_3$ -Koordinaten der Punkte $F$ und $D$ gleich $6$ ist.
Setze die Werte für $G$ und $h$ in die Volumenformel ein:
Das Gesamtvolumen des Körpers $ABCDEF$ ist dann:
$V_{\text{gesamt}}=V_{\text{Prisma}}+V_{\text{Pyramide}}=(81+27)\;\text{VE}=108\;\text{VE}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Körper setzt sich aus zwei Teilen zusammen, ein dreiseitiges Prisma und eine dreiseitige Pyramide.
Berechne jeweils das Volumen der beiden Körper und addiere dann die beiden Volumina.

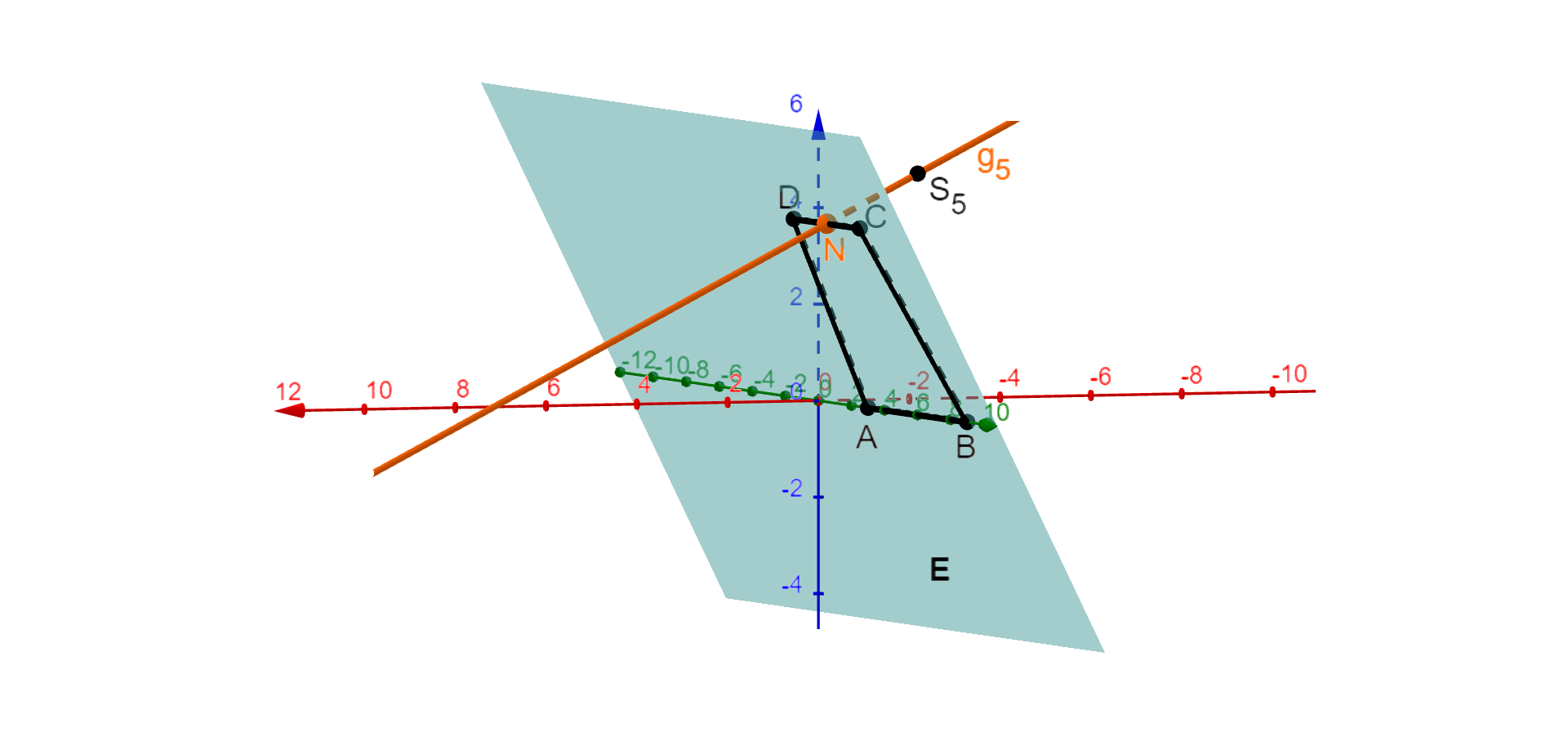
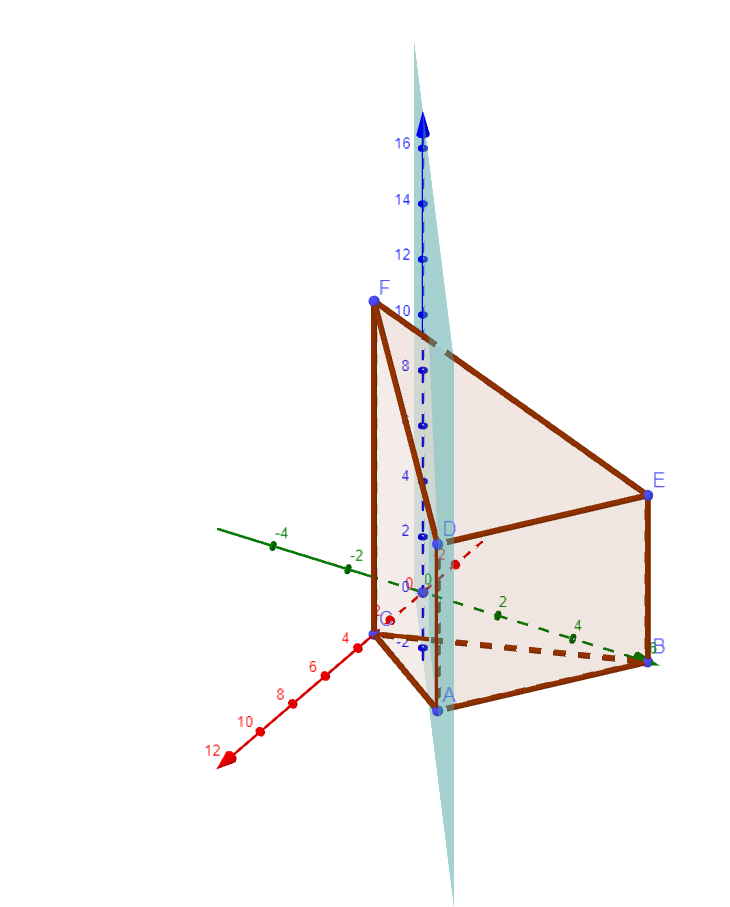
Die Ebene $N_{k}$ enthält die $x_{3}$ -Achse und den Punkt $P_{k}(1-k|k| 0)$ mit $0<k<1$ .

Welche Kanten des Körpers von $N_{k}$ geschnitten werden, ist abhängig von $k$ . Die Abbildung 2 zeigt die Situation für $k=0{,}8$ .

Nennen Sie für $k=0{,}8$ die Kanten, die geschnitten werden.

Durchläuft $k$ alle Werte zwischen 0 und 1, so gibt es Bereiche $a<k<b$ , in denen $N_{k}$ für alle Werte von $k$ jeweils die gleichen Kanten des Körpers schneidet.

Bestimmen Sie den größten dieser Bereiche. (6 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene

Kanten für $k=0{,}8$ , die geschnitten werden

Betrachtet man die Abbildung, so erkennt man, dass die Kanten $\overline{AB}$ , $\overline{DE}$ , $\overline{BC}$ und $\overline{EF}$ geschnitten werden.

Der größte dieser Bereiche

Interessant ist die Ebene $N_k$ ⁣, die durch den Punkt $A$ verläuft.

Für welches $k$ enthält die Ebene $N_k$ den Punkt $A(6|3|0)$ ?

Man erstellt eine Geradengleichung $g_{OA}$ , die durch den Ursprung verläuft und den Punkt A enthält.

$g_{OA}:\:\vec X=r\cdot \begin{pmatrix}6\\3\\0\end{pmatrix}$

Der Punkt $P_k$ soll auf der Geraden $g_{OA}$ liegen:

$P_k\cap g_{OA}$

\displaystyle \begin{pmatrix}1-k\\k\\0\end{pmatrix}

=

\displaystyle r\cdot \begin{pmatrix}6\\3\\0\end{pmatrix}

Es ergeben sich zwei Gleichungen:

$\mathrm{(I)}:\; 1-k=6r\;\Rightarrow\;\mathrm{(I')}:\;r=\dfrac{1-k}{6}$

$\mathrm{(II)}:\;k=3r\;\;\;\;\;\;\Rightarrow\;\mathrm{(II')}:\;r=\dfrac{k}{3}$

Aus $\mathrm{(I')}=\mathrm{(II')}$ folgt:

$\displaystyle \dfrac{1-k}{6}$	$=$	$\displaystyle \dfrac{k}{3}$	$\displaystyle \cdot 6$
	↓	Löse nach $k$ auf.
$\displaystyle 1-k$	$=$	$\displaystyle 2\cdot k$	$\displaystyle +k$
$\displaystyle 1$	$=$	$\displaystyle 3\cdot k$	$\displaystyle :3$
$\displaystyle \dfrac{1}{3}$	$=$	$\displaystyle k$

Für $k=\frac{1}{3}$ verläuft die Ebene $N_{\frac{1}{3}}$ durch den Punkt $A$ .

Diese Ebene ist in der folgenden Abbildung dargestellt. (Die Abbildung ist nicht Teil der Aufgabenstellung, sie dient nur zur Veranschaulichung.)

Durchläuft nun $k$ die Werte von $0$ bis $1$ , dreht sich die Ebene $N_k$ um die $x_3$ -Achse.

Dabei werden zwei verschiedene Bereiche $]a;b[$ durchlaufen, sodass die Ebene $N_k$ für alle Werte von $k$ aus $]a;b[$ die gleichen Kanten des Körpers schneidet.

Der erste Bereich ist das Intervall $]0;\frac{1}{3}[$ mit einer Intervalllänge von $\frac{1}{3}$ , der zweite Bereich ist das Intervall $]\frac{1}{3};1[$ mit einer Intervalllänge von $\frac{2}{3}$ .

Gesucht ist der größere Bereich, also hier das Intervall $]\frac{1}{3};1[$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

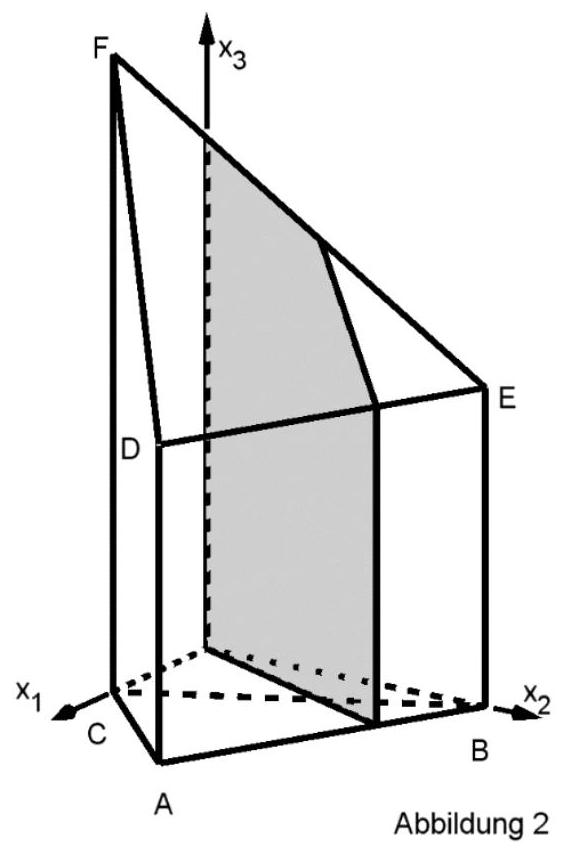
Auf der Kante $\overline{A D}$ liegt der Punkt $Q$ , auf der Kante $\overline{B E}$ der Punkt $R(0|6| 2)$ . Das Dreieck $F Q R$ hat in $Q$ einen rechten Winkel.

Bestimmen Sie die $x_{3}$ -Koordinate von $Q$ . (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt

$x_3$ Koordinate von Q

Das Dreieck $FQR$ hat in $Q$ einen rechten Winkel. Daher gilt:

$\overrightarrow{QR}\perp \overrightarrow{QF}\;\Rightarrow\;\overrightarrow{QR}\circ\overrightarrow{QF}=0$

Der Punkt $Q$ hat dieselben $x_1$ - und $x_2$ -Koordinaten wie der Punkt $A$ .

$\Rightarrow\;Q(6|3|q_3)$

Berechne die Vektoren $\overrightarrow{QR}$ und $\overrightarrow{QF}$ :

$\overrightarrow{QR}=\vec R-\vec Q=\begin{pmatrix}0\\6\\2\end{pmatrix}-\begin{pmatrix}6\\3\\q_3\end{pmatrix}=\begin{pmatrix}-6\\3\\2-q_3\end{pmatrix}$

$\overrightarrow{QF}=\vec F-\vec Q=\begin{pmatrix}3\\0\\12\end{pmatrix}-\begin{pmatrix}6\\3\\q_3\end{pmatrix}=\begin{pmatrix}-3\\-3\\12-q_3\end{pmatrix}$

$\displaystyle \overrightarrow{QR}\circ\overrightarrow{QF}$	$=$	$\displaystyle 0$
	↓	Setze die Vektoren ein.
$\displaystyle \begin{pmatrix}-6\\3\\2-q_3\end{pmatrix}\circ\begin{pmatrix}-3\\-3\\12-q_3\end{pmatrix}$	$=$	$\displaystyle 0$
	↓	Berechne das Skalarprodukt.
$\displaystyle (-6)\cdot(-3)+3\cdot (-3)+(2-q_3)\cdot(12-q_3)$	$=$	$\displaystyle 0$
	↓	Vereinfache.
$\displaystyle 18-9+24-2q_3-12q_3+q_3^2$	$=$	$\displaystyle 0$
	↓	Fasse zusammen.
$\displaystyle q_3^2-14q_3+33$	$=$	$\displaystyle 0$

Lösen der quadratischen Gleichung

Die erhaltene quadratische Gleichung kann mit der Mitternachtsformel (abc-Formel) oder mit der pq-Formel gelöst werden.

Hier erfolgt die Lösung mit der pq-Formel. Die Werte für $p$ und $q$ werden abgelesen: $p=-14$ und $q=33$

$\displaystyle q_{3_{1{,}2}}$	$=$	$\displaystyle -\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q}$
	↓	Setze $p$ und $q$ ein.
	$=$	$\displaystyle -\dfrac{(-14)}{2}\pm\sqrt{\left(\dfrac{-14}{2}\right)^2-33}$
	↓	Vereinfache.
	$=$	$\displaystyle 7\pm\sqrt{49-33}$
	↓	Fasse zusammen.
	$=$	$\displaystyle 7\pm\sqrt{16}$
	↓	Ziehe die Wurzel.
	$=$	$\displaystyle 7\pm4$

$q_3$ ist somit entweder $11$ oder $3$ . Die Lösung $q_3=11$ entfällt, da $q_3$ zwischen $0$ und $6$ liegen muss ( $A$ hat die $x_3$ -Koordinate $0$ und $D$ hat die $x_3$ -Koordinate $6$ ).

Die $q_3$ -Koordinate von $Q$ ist also $3$ und der Punkt $Q$ hat die Koordinaten $Q(6|3|3)$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

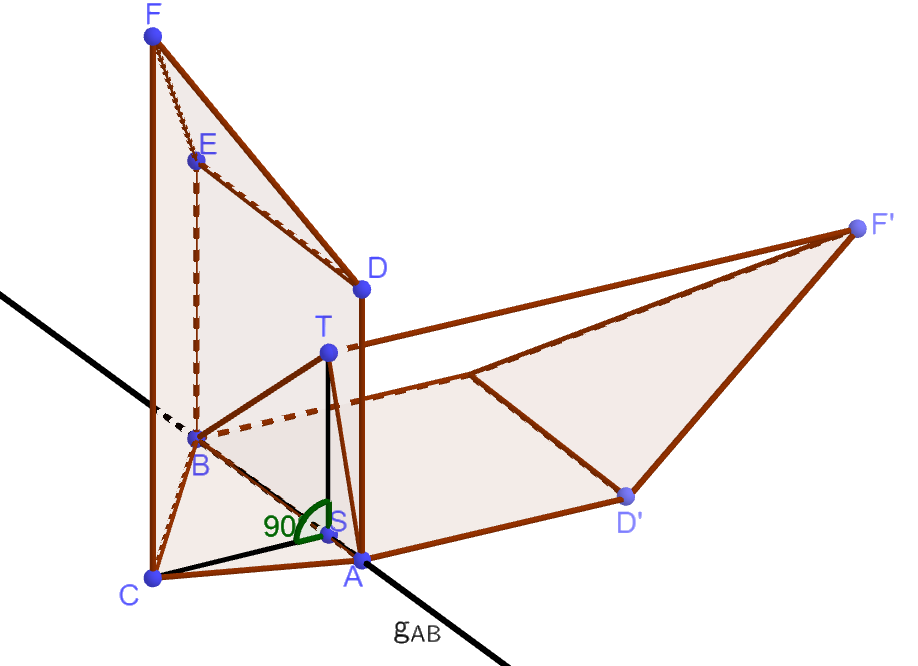
Der Körper wird so um die Gerade durch $A$ und $B$ gedreht, dass der mit $D$ bezeichnete Eckpunkt nach der Drehung in der $x_{1} x_{2}$ -Ebene liegt und dabei eine positive $x_{2}$ -Koordinate hat. Die folgenden Rechnungen liefern die Lösung einer Aufgabe im Zusammenhang mit der beschriebenen Drehung:
$\overrightarrow{A B} \cdot[(\overrightarrow{O A}+s \cdot \overrightarrow{A B})-\overrightarrow{O C}]=0$ liefert die Lösung $s=0{,}2$ , d. h. $S(4{,}8|3{,}6| 0)$
$\def\arraystretch{1.25} \overrightarrow{O T}=\overrightarrow{O S}+|\overrightarrow{C S}| \cdot\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right)$
Formulieren Sie eine passende Aufgabenstellung.
Geben Sie die Bedeutung von $S$ an. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lotfußpunktverfahren
Passende Aufgabenstellung
Was wird berechnet?
Der Ausdruck $\overrightarrow{A B} \cdot[(\overrightarrow{O A}+s \cdot \overrightarrow{A B})-\overrightarrow{O C}]=0$ ist gegeben.
Es handelt sich hier um ein Skalarprodukt, das gleich null ist. Die beiden beteiligten Vektoren müssen also senkrecht aufeinander stehen.
Der erste Vektor ist der Vektor $\overrightarrow{A B}$ , der Richtungsvektor der Geraden durch die Punkte $A$ und $B$ .
Man betrachtet nun den Vektor in der eckigen Klammer. Es handelt sich um die Differenz zwischen einem beliebigen Punkt $S$ auf der Geraden $g_{AB}$ durch die Punkte A und B und dem Vektor $\overrightarrow{OC}$ .
Dabei ist die Gerade $g_{AB}$ gegeben durch:
$g_{AB}:\;\overrightarrow{OX}=\overrightarrow{O A}+s \cdot \overrightarrow{A B}$
Die eckige Klammer stellt somit den Vektor $\overrightarrow{CS}$ dar.
Es ist also: $\overrightarrow {AB}\circ \overrightarrow {CS}=0 \;\Rightarrow\;\overrightarrow {AB}\perp\overrightarrow {CS}$
Die Lösung der Gleichung $\overrightarrow {AB}\circ \overrightarrow {CS}=0$ liefert für $s$ den Wert $s=0{,}2$ .
Einsetzen von $s=0{,}2$ in die Geradengleichung $g_{AB}$ ergibt die Koordinaten des Lotfußpunktes $S(4{,}8|3{,}6|0)$ .
Für den Punkt $T$ gilt die Gleichung:
$\overrightarrow{OT}=\overrightarrow{OS} +\left|\overrightarrow {CS}\right|\cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$
Die folgende Abbildung verdeutlicht diese Gleichung.
Der Punkt $C$ wird um $90^\circ$ gedreht, sodass der Punkt $T$ entsteht.
Dabei ist $\Big\vert\overrightarrow{CS}\Big\vert=\Big\vert\overrightarrow{ST}\Big\vert$ .
Aber der Vektor $\overrightarrow{ST}$ steht senkrecht auf dem Vektor $\overrightarrow{CS}$ . Deshalb muss zum $\overrightarrow{OS}$ der Vektor $\left|\overrightarrow {CS}\right|\cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$ addiert werden, um zum Vektor $\overrightarrow{OT}$ zu kommen.
Skizze
Aufgabenstellung
Der Punkt $T$ entsteht aus dem Punkt $C$ durch Rotation des Körpers um die Gerade $g_{AB}$ um $90^\circ$ . Gesucht sind die Koordinaten des Punktes $T$ .
Bedeutung von S
Der Punkt $S$ ist der Punkt auf der Kante $\overline{AB}$ mit dem kürzesten Abstand von $C$ . ( $S$ ist der Lotfußpunkt von $C$ auf die Gerade $g_{AB}$ .)
Hinweis: Die folgende Abbildung dient nur zur Veranschaulichung. Sie ist nicht Teil der Aufgabenstellung.
Skizze
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Untersuche die einzelnen Teile des Ausdrucks $\overrightarrow{A B} \cdot[(\overrightarrow{O A}+s \cdot \overrightarrow{A B})-\overrightarrow{O C}]=0$ .
Die Lösung dieser Gleichung ergibt einen Wert für $s$ und einen Punkt $S$ .
Mit diesem Punkt $S$ und dem Punkt $C$ wird ein weiterer Vektor $\overrightarrow{O T}$ berechnet.
Welche Bedeutung hat der Vektor $\overrightarrow{O T}$ ?

$\displaystyle l(x)$	$=$	$\displaystyle 2{,}53 \cdot\left(e^{\frac{1}{11} \cdot(32-(-x))}-1\right)$
	↓	Berechne die Klammer.
	$=$	$\displaystyle 2{,}53 \cdot\left(e^{\frac{1}{11} \cdot(32+x)}-1\right)$

$\displaystyle 0{,}15$	$>$	$\displaystyle 0{,}1+1{,}96\cdot\frac{\sqrt{ 0{,}1\cdot0{,}9}}{\sqrt{n}}$	$\displaystyle -0{,}1$
	↓	Löse nach $n$ auf.
$\displaystyle 0{,}05$	$>$	$\displaystyle 1{,}96\cdot\frac{\sqrt{ 0{,}1\cdot0{,}9}}{\sqrt{n}}$	$\displaystyle \cdot \sqrt{n}$
	↓	Vereinfache.
$\displaystyle 0{,}05\cdot \sqrt{n}$	$>$	$\displaystyle 0{,}588$	$\displaystyle :0{,}05$
$\displaystyle \sqrt{n}$	$>$	$\displaystyle \dfrac{0{,}588}{0{,}05}$
	↓	Vereinfache.
$\displaystyle \sqrt{n}$	$>$	$\displaystyle 11{,}76$	$\displaystyle ()^2$
$\displaystyle n$	$>$	$\displaystyle 138{,}2976$

$\displaystyle 0{,}778$	$=$	$\displaystyle 0{,}45\cdot 0{,}8+0{,}55\cdot a$
	↓	Löse nach $a$ auf.
$\displaystyle 0{,}778$	$=$	$\displaystyle 0{,}36+0{,}55\cdot a$	$\displaystyle -0{,}36$
$\displaystyle 0{,}418$	$=$	$\displaystyle 0{,}55 \cdot a$	$\displaystyle :0{,}55$
$\displaystyle \dfrac{0{,}418}{0{,}55}$	$=$	$\displaystyle a$
$\displaystyle 0{,}76$	$=$	$\displaystyle a$

$\displaystyle 0{,}5+ 0{,}001\cdot x+0{,}1$	$=$	$\displaystyle 0{,}8$
	↓	Löse nach $x$ auf.
$\displaystyle 0{,}6+0{,}001\cdot x$	$=$	$\displaystyle 0{,}8$	$\displaystyle -0{,}6$
$\displaystyle 0{,}001\cdot x$	$=$	$\displaystyle 0{,}2$	$\displaystyle :0{,}001$
$\displaystyle x$	$=$	$\displaystyle \dfrac{0{,}2}{0{,}001}$
$\displaystyle x$	$=$	$\displaystyle 200$

$\displaystyle n\cdot 0{,}985$	$>$	$\displaystyle 780$	$\displaystyle :0{,}985$
$\displaystyle n$	$>$	$\displaystyle \dfrac{780}{0{,}985}$
$\displaystyle n$	$>$	$\displaystyle 791{,}88$
$\displaystyle n$	$≥$	$\displaystyle 792$

$\displaystyle 0$	$=$	$\displaystyle 20 \cdot \cos (x-2)$	$\displaystyle :20$
$\displaystyle 0$	$=$	$\displaystyle \cos (x-2)$

$\displaystyle 0$	$=$	$\displaystyle 2{,}53 \cdot\left(e^{\frac{1}{11} \cdot(32-x)}-1\right)$	$\displaystyle :2{,}53$
	$=$	$\displaystyle e^{\frac{1}{11} \cdot(32-x)}-1$	$\displaystyle +1$
$\displaystyle 1$	$=$	$\displaystyle e^{\frac{1}{11} \cdot(32-x)}$

Wahlteil - CAS

Aufgabe 1A

Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat

Begründung mit dem Funktionsterm

Hast du eine Frage oder Feedback?

Maximale Änderungsrate

Wo liegt die stärkste Zunahme?

Wert der momentanen Änderungsrate zur Zeit der stärksten Zunahme

Hast du eine Frage oder Feedback?

Maximale Staulänge

Hast du eine Frage oder Feedback?

Die Staulänge kann für jeden Zeitpunkt von 6:006:006:00 Uhr bis 10:0010:0010:00 Uhr durch die Funktion sss angegeben werden.

Hast du eine Frage oder Feedback?

Zunahme der Staulänge

Mittlere Änderungsrate der Staulänge für diesen Zeitraum

Hast du eine Frage oder Feedback?

Gleichsetzen der Funktionen

Gemeinsame Punkte

Hast du eine Frage oder Feedback?

Lösung

Geradengleichung ggg

Rotationsvolumen

Hast du eine Frage oder Feedback?

Wert von kkk⁣, für den der Graph von hk′h_k'hk′​ Tangente an den Graphen von hkh_khk​ ist

Hast du eine Frage oder Feedback?

Aufgabe 1B

Berechnung der 1. und 2. Ableitung

Setze f′′(x)=0f''(x)=0f′′(x)=0

Bestimmung der Steigung in diesem Wendepunkt

Hast du eine Frage oder Feedback?

Schnittpunkte mit den beiden Koordinatenachsen

Begründung, dass der gemeinsame Punkt mit der x-Achse der Tiefpunkt des Graphen von f ist

Hast du eine Frage oder Feedback?

Bestimmung der Extrempunkte

Geradengleichung

Gleichschenkliges Dreieck

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Bestimmung des Maximums von k(x)k(x)k(x)

Hast du eine Frage oder Feedback?

Bestimmung Punkt BBB

Differenz xA−xBx_A-x_BxA​−xB​

Hast du eine Frage oder Feedback?

Berechnung des Mittelwerts

Hast du eine Frage oder Feedback?

Aufgabe 1C

Länge der Fahrbahn

Hast du eine Frage oder Feedback?

Term l(x)l(x)l(x) für das Abspannseil (links)

Intervall, in dem dieser Term das Abspannseil darstellt.

Hast du eine Frage oder Feedback?

Länge eines Pfeilers oberhalb der Fahrbahn.

Hast du eine Frage oder Feedback?

Größe des Winkels, unter dem das rechte Abspannseil auf den rechten Pfeiler trifft

Hast du eine Frage oder Feedback?

Abstand der vertikalen Begrenzung zum Pfeiler.

Hast du eine Frage oder Feedback?

Symmetrie des Graphen

Hast du eine Frage oder Feedback?

Bedeutung des Terms im Sachzusammenhang

Hast du eine Frage oder Feedback?

Abstand von Q zum Tragseil

Hast du eine Frage oder Feedback?

Summe der Streckenlängen

Begründung, dass die Länge des Tragseils größer ist als die Summe der Streckenlängen in der Realität

Hast du eine Frage oder Feedback?

Aufgabe 2A

A: "Es wird genau siebenmal eine ungerade Zahl erzielt".

B: "Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt".

Hast du eine Frage oder Feedback?

C: "Die Summe der erzielten Zahlen ist kleiner als 444".

D: "Das Produkt der erzielten Zahlen ist 222 oder 333".

Ereignisse CCC und DDD stochastisch unabhängig

Hast du eine Frage oder Feedback?

Auszahlungsbeträge und Wahrscheinlichkeiten

Erwartungswert

Hast du eine Frage oder Feedback?

Erwartungswert

Bestimmung der Werte

Die Staulänge kann für jeden Zeitpunkt von $6:00$ Uhr bis $10:00$ Uhr durch die Funktion $s$ angegeben werden.

Geradengleichung $g$

Wert von $k$ ⁣, für den der Graph von $h_k'$ Tangente an den Graphen von $h_k$ ist

Setze $f''(x)=0$

Bestimmung des Maximums von $k(x)$

Bestimmung Punkt $B$

Differenz $x_A-x_B$

Term $l(x)$ für das Abspannseil (links)

C: "Die Summe der erzielten Zahlen ist kleiner als $4$ ".

D: "Das Produkt der erzielten Zahlen ist $2$ oder $3$ ".

Ereignisse $C$ und $D$ stochastisch unabhängig

Es gibt zwei, aber nicht drei aufeinanderfolgende Werte von $n$

Berechnung des Wertes $n$

Bestimmung von $a$

Vergleiche im Baumdiagramm die entsprechenden Pfade, die zu $Z$ führen

Wert für $a$ bei stochastischer Unabhängigkeit

Löse die Gleichung mit $\text{binomCdf}$ .

Weniger als zwei Flaschen mit weniger als $600\; \mathrm{ml}$ Öl enthalten

Wahrscheinlichkeit, dass mehr als $3\;\%$ der Kartons fehlerhaft sind

$A$ : „Die Flasche enthält mehr als $601 \mathrm{ml}$ Öl.“

$B$ : „Die Füllmenge der Flasche weicht höchstens um $0{,}5\; \mathrm{ml}$ vom Erwartungswert ab.“

Systematisches Probieren von $\sigma$