Aufgabe 2C
Ein Unternehmen stellt Olivenöl her und füllt es in Flaschen ab. Laut Aufdruck beträgt die Füllmenge jeder Flasche .
Für jede Flasche beträgt die Wahrscheinlichkeit dafür, dass sie weniger als Öl enthält, . Die Anzahl der Flaschen mit weniger als Öl wird durch eine Binomialverteilung beschrieben. Die Flaschen werden in Kartons verpackt. Jeder Karton enthält zwölf Flaschen.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass in einem Karton weniger als zwei Flaschen mit weniger als Öl enthalten sind. (2 BE)
An einen Supermarkt wird regelmäßig die gleiche Anzahl von Flaschen geliefert. Dabei enthalten im Mittel mehr als 780 Flaschen mindestens Öl. Ermitteln Sie, wie viele Flaschen mindestens geliefert werden. (4 BE)
Ein Karton gilt als fehlerhaft, wenn mehr als eine Flasche weniger als Öl enthält.
Ein Supermarkt erhält eine Lieferung von 150 Kartons.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass mehr als der Kartons fehlerhaft sind. (4 BE)
Die Füllmenge der Flaschen ist normalverteilt mit einem Erwartungswert von und einer Standardabweichung von .
Eine Flasche wird zufällig ausgewählt.
Ermitteln Sie für die folgenden Ereignisse jeweils die Wahrscheinlichkeit: (4 BE)
: „Die Flasche enthält mehr als Öl.“
: „Die Füllmenge der Flasche weicht höchstens um vom Erwartungswert ab.“
Das Unternehmen möchte die Wahrscheinlichkeit dafür, dass eine Flasche weniger als Öl enthält, verringern. Für die nötige Änderung der Maschine, die die Flaschen befüllt, gibt es zwei Vorschläge:
Vorschlag 1: Die eingestellte Füllmenge von wird erhöht.
Vorschlag 2: Die Genauigkeit, mit der die eingestellte Füllmenge von erreicht wird, wird erhöht.
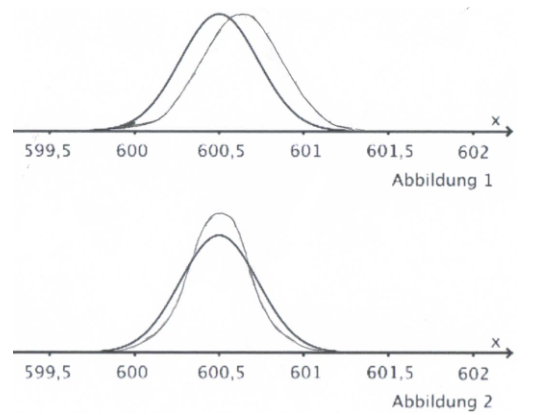
Beide Abbildungen zeigen jeweils den Graphen der Dichtefunktion, die vor der Änderung der Maschine die Füllmenge der Flaschen beschreibt.
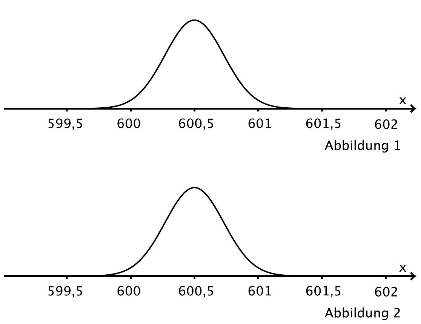
Skizzieren Sie in der Abbildung 1 den Graphen einer Dichtefunktion, die zu Vorschlag 1 passt und in der Abbildung 2 den Graphen einer Dichtefunktion, die zum Vorschlag 2 passt.
Begründen Sie für Vorschlag 1, dass damit das Ziel des Unternehmens erreicht wird.
(7 BE)
Bestimmen Sie die größtmögliche Standardabweichung mit einer Genauigkeit von drei Nachkommastellen, für die gilt: (4 BE)
Die Wahrscheinlichkeit dafür, dass eine Flasche weniger als Öl enthält, ist höchstens halb so groß.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?