Wahlteil - CAS - lernen mit Serlo!

Aufgabe 3A

Auf einem ebenen, horizontalen Gelände steht ein $15 \mathrm{~m}$ hoher Mast, an dem drei rechteckige Werbeflächen befestigt sind. In der Abbildung 1 ist eine der Werbeflächen grau dargestellt. Der Mast ist zylinderförmig und hat einen Durchmesser von $80 \mathrm{~cm}$ . Er verläuft ebenso wie die seitlichen Kanten der Werbeflächen vertikal.

In einem Koordinatensystem wird das Gelände durch die $x_1x_2$ -Ebene beschrieben. Eine Längeneinheit im Koordinatensystem entspricht $1$ m in der Wirklichkeit. Der Mittelpunkt der Grundfläche des Masts wird durch den Koordinatenursprung dargestellt. Die Punkte $A(5\mid-2\mid 11),B(-2\mid5\mid11),C,D(5\mid -2\mid 15),E(-2\mid 5\mid 15)$ und $F(-2\mid -2\mid 15)$ stellen Eckpunkte der Werbeflächen dar.

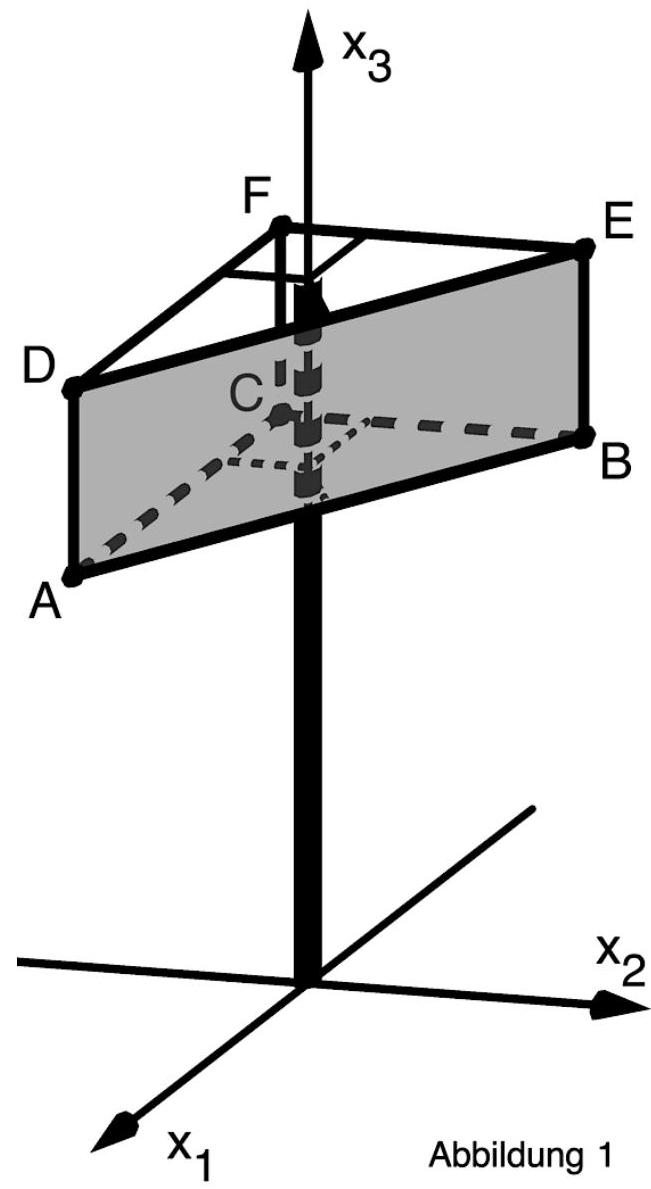
Bestimmen Sie den Flächeninhalt der grau dargestellten Werbefläche.
Untersuchen Sie, ob die beiden anderen Werbeflächen einen rechten Winkel einschließen. (6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
Flächeninhalt der grau dargestellten Werbefläche
Berechne die Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AD}$ .
$\overrightarrow{AB}=\begin{pmatrix}-2\\5\\11\end{pmatrix}-\begin{pmatrix}5\\-2\\11\end{pmatrix}=\begin{pmatrix}-7\\7\\0\end{pmatrix}$
$\overrightarrow{AD}=\begin{pmatrix}5\\-2\\15\end{pmatrix}-\begin{pmatrix}5\\-2\\11\end{pmatrix}=\begin{pmatrix}0\\0\\4\end{pmatrix}$
Senkrechte Vektoren
Prüfe, ob die beiden Vektoren senkrecht aufeinander stehen.
In diesem Fall handelt es sich um ein Rechteck.
Da das Skalarprodukt gleich null ist, stehen die beiden Vektoren senkrecht aufeinander.
$A_\square=\left|\overrightarrow{AB}\right| \cdot \left|\overrightarrow{AD}\right|=\sqrt{(-7)^2+7^2+0}\cdot \sqrt{0^2+0^2+4^2}=\sqrt{2\cdot49}\cdot 4=28\cdot \sqrt{2}$
$A_\square=28\cdot \sqrt{2}\approx39{,}6\;\text{m}^2$
Der Flächeninhalt der grau dargestellten Werbefläche beträgt etwa $39{,}6\;\text{m}^2$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne die Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AD}$ .
Prüfe, ob die beiden Vektoren senkrecht aufeinander stehen. In diesem Fall handelt es sich um ein Rechteck.
$A_\square=\left|\overrightarrow{AB}\right| \cdot \left|\overrightarrow{AD}\right|$
Die grau dargestellte Werbefläche liegt in einer Ebene, deren Gleichung in der Form $a \cdot x_{1}+a \cdot x_{2}=b$ dargestellt werden kann.
Ermitteln Sie passende Werte von $a$ und $b$ . (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebenengleichung aufstellen
Einsetzen der Koordinaten
Gegeben ist die Ebenengleichung $a \cdot x_{1}+a \cdot x_{2}=b$ .
Setze die Koordinaten des Punktes $A$ ein.
Demnach ist z.B. $a$ frei wählbar.
Setze $a=1$ , dann ist $b=3\cdot 1=3$
Passende Werte von a und b
Passende Werte von $a$ und $b$ sind $a=1$ und $b=3$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Gegeben ist die Ebenengleichung $a \cdot x_{1}+a \cdot x_{2}=b$ .
Setze die Koordinaten des Punktes $A$ ein. Du erhältst eine Gleichung für $a$ und $b$ .
Demnach ist z.B. $a$ frei wählbar, also z.B. $a=1$ . Dann kann auch $b$ angegeben werden.
Begründen Sie, dass der Abstand der grau dargestellten Werbefläche zum Mast mit dem Abstand des Mittelpunkts der oberen Kante dieser Werbefläche zum Mast übereinstimmt. (5 BE)
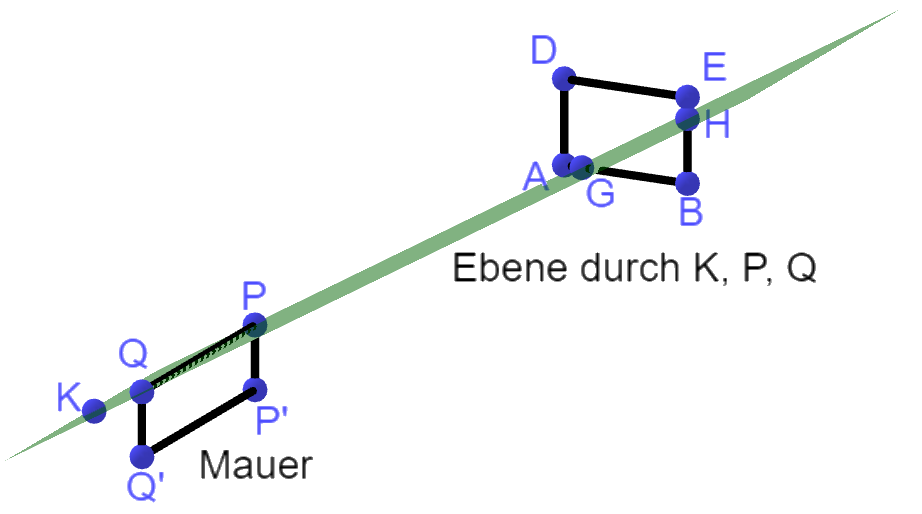
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
Abstand der grau dargestellten Werbefläche zum Mast
Die Gleichung der grauen Ebene ist $E: \; x_1+x_2=3$ .
Die Ebene verläuft parallel zur $x_3$ -Achse. Der Mast verläuft entlang der $x_3$ -Achse (Symmetrieachse des Mastes).
Kein Punkt des Vierecks $ABCD$ hat einen kleineren Abstand zur $x_3$ -Achse als der Mittelpunkt $M$ der Strecke $\overline{DE}$ .
Die folgende Abbildung ist in der Aufgabenstellung nicht gefordert. Sie dient nur zur Veranschaulichung.
Skizze
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Betrachte die besondere Lage der Ebene $E$ .
Vergleiche mit der Lage des Mastes.
Beachte, um was für ein Dreieck es sich beim Dreieck $DEF$ handelt.
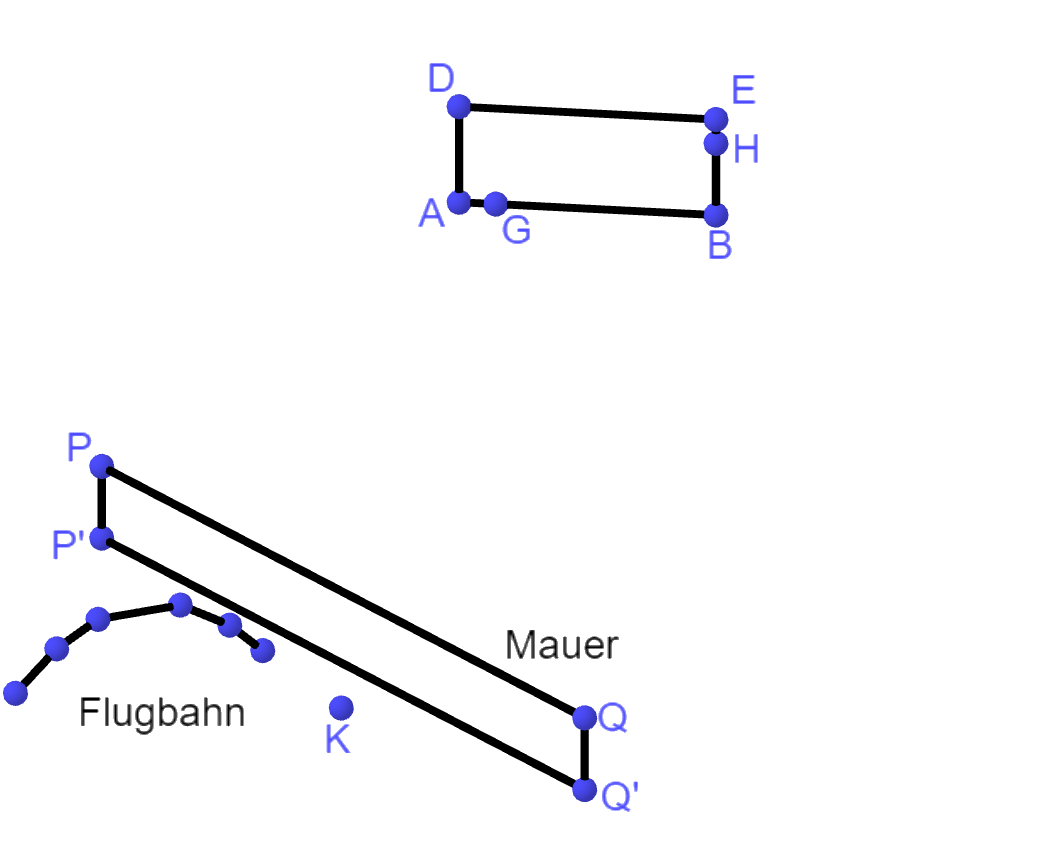
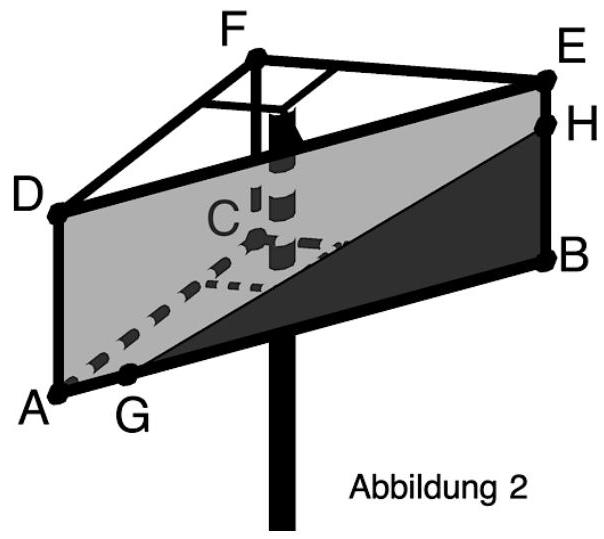
Auf dem Gelände befindet sich ein Sportplatz. Von dort aus blickt ein Kind zur grau dargestellten Werbefläche. Die Sicht des Kindes wird durch eine Mauer eingeschränkt. Die obere Kante der Mauer wird durch die Strecke zwischen den Punkten $P(20|-5| 3)$ und $Q(20|25| 3)$ dargestellt. Der Punkt, von dem der Blick des Kindes ausgeht, wird durch $K(24|15| 1)$ beschrieben. Das Kind kann denjenigen Teil der Werbefläche, der durch das Dreieck $G B H$ mit $G(4|-1| 11)$ dargestellt wird, nicht sehen (siehe Abbildung 2).
Eine Sichtlinie verläuft von $K$ zu $G$ .
Berechnen Sie die Größe des Winkels dieser Sichtlinie gegenüber dem horizontalen Gelände. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen Vektoren, Geraden und Ebenen
Größe des Winkels dieser Sichtlinie gegenüber dem horizontalen Gelände
Berechne den Vektor $\overrightarrow {KG}=\begin{pmatrix}4\\-1\\11\end{pmatrix}-\begin{pmatrix}24\\15\\1\end{pmatrix}=\begin{pmatrix}-20\\-16\\10\end{pmatrix}=2\cdot \begin{pmatrix}-10\\-8\\5\end{pmatrix}$ .
Der Normalenvektor der $x_1x_2$ -Ebene ist $\vec n=\begin{pmatrix}0\\0\\1\end{pmatrix}$ .
Dann gilt für den Winkel:
$\sin\alpha=\dfrac{\left|\begin{pmatrix}-10\\-8\\5\end{pmatrix}\circ\begin{pmatrix}0\\0\\1\end{pmatrix}\right|}{\sqrt{(-10)^2+(-8)^2+5^2}\cdot 1}=\dfrac{5}{\sqrt{189}}$
$\alpha=\sin^{-1}\left(\dfrac{5}{\sqrt{189}}\right)\approx21{,}3^\circ$
Die Größe des Winkels dieser Sichtlinie gegenüber dem horizontalen Gelände beträgt rund $21{,}3^\circ$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne den Vektor $\overrightarrow {KG}$ .
Der Normalenvektor der $x_1x_2$ -Ebene ist $\vec n=\begin{pmatrix}0\\0\\1\end{pmatrix}$ .
Dann gilt für den gesuchten Winkel: $\sin\alpha=\dfrac{\left|\overrightarrow {KG}\circ \vec n\right|}{\left|\overrightarrow {KG}\right|\cdot|\vec n|}$
Berechnen Sie die Koordinaten von $H$ . (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene aus drei Punkten
Aufstellen der Ebene
Erstelle die Gleichung einer Ebene $E$ durch die drei Punkte $KPQ$ und schneide sie mit der Geraden $g$ , die durch die Punkte $B$ und $E$ verläuft.
$E_{KPQ}:\; \vec x=\overrightarrow {OK}+r\cdot \overrightarrow {KP}+s\cdot \overrightarrow {KQ}$
$E_{KPQ}:\; \vec x=\begin{pmatrix}24\\15\\1\end{pmatrix}+r\cdot \left(\begin{pmatrix}20\\-5\\3\end{pmatrix}-\begin{pmatrix}24\\15\\1\end{pmatrix}\right)+s\cdot \left(\begin{pmatrix}20\\25\\3\end{pmatrix}-\begin{pmatrix}24\\15\\1\end{pmatrix}\right)$
$E_{KPQ}:\; \vec x=\begin{pmatrix}24\\15\\1\end{pmatrix}+r\cdot \begin{pmatrix}-4\\-20\\2\end{pmatrix}+s\cdot \begin{pmatrix}-4\\10\\2\end{pmatrix}$
Gerade $g: \;\vec x=\overrightarrow {OB}+t\cdot\overrightarrow {BE}=\begin{pmatrix}-2\\5\\11\end{pmatrix}+t\cdot \left(\begin{pmatrix}-2\\5\\15\end{pmatrix}-\begin{pmatrix}-2\\5\\11\end{pmatrix}\right)$
$g: \;\vec x=\begin{pmatrix}-2\\5\\11\end{pmatrix}+t\cdot \begin{pmatrix}0\\0\\4\end{pmatrix}$
oder mit verkürztem Richtungsvektor
$g: \;\vec x==\begin{pmatrix}-2\\5\\11\end{pmatrix}+t\cdot \begin{pmatrix}0\\0\\1\end{pmatrix}$
Schnitt von Gerade und Ebene
Wir schneiden die Gerade und die Ebene: $g\cap E$
$\begin{pmatrix}24\\15\\1\end{pmatrix}+r\cdot \begin{pmatrix}-4\\-20\\2\end{pmatrix}+s\cdot \begin{pmatrix}-4\\10\\2\end{pmatrix}=\begin{pmatrix}-2\\5\\11\end{pmatrix}+t\cdot \begin{pmatrix}0\\0\\1\end{pmatrix}$
Der GTR-Rechner liefert die Lösung: $t=3$ .
Koordinaten von H
Setze $t=3$ in $g$ ein. Du erhältst die Koordinaten von $H$ .
$\overrightarrow {OH}=\begin{pmatrix}-2\\5\\11\end{pmatrix}+3\cdot \begin{pmatrix}0\\0\\1\end{pmatrix}=\begin{pmatrix}-2+0\\5+0\\11+3\end{pmatrix}=\begin{pmatrix}-2\\5\\14\end{pmatrix}\;\Rightarrow\;H(-2|5|14)$
Der Punkt $H$ hat die Koordinaten $H(-2|5|14)$ .
Anmerkung: Die folgende Abbildung ist nicht in der Aufgabe gefordert. Sie dient nur zur Veranschaulichung.
Skizze
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Erstelle die Gleichung einer Ebene $E$ durch die drei Punkte $KPQ$ .
Schneide die Ebene $E$ mit der Geraden $g$ , die durch die Punkte $B$ und $E$ verläuft.
Auf dem Sportplatz wird ein Fußball geschossen. Die Flugbahn des Balls wird durch Punkte der Form $\left(32-8 t|5|-5 t^{2}+6{,}5 t+0{,}3\right)$ mit $t \geq 0$ beschrieben. Dabei ist $t$ die seit dem Schuss vergangene Zeit in Sekunden.
Beschreiben Sie, wie man ermitteln könnte, ob der Ball die Mauer trifft, bevor er den Boden berührt. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor
Beschreibung wie man ermitteln könnte, ob der Ball die Mauer trifft
Jeder Punkt der Mauer hat die $x_1$ -Koordinate $20$ .
Die Flugbahn des Balls wird durch Punkte der Form $\left(32-8 t|5|-5 t^{2}+6{,}5 t+0{,}3\right)$ beschrieben.
Daraus ergibt sich die Gleichung: $32-8\cdot t=20\;\Rightarrow\;t_1$
Da die Mauer eine Höhe von $3$ Metern hat, kann der Ball die Mauer nur treffen, wenn gilt: $0<-5\cdot t_1^{2}+6{,}5\cdot t_1+0{,}3 \leq 3$ .
Anmerkung: Die folgende Abbildung ist nicht in der Aufgabe gefordert. Sie dient nur zur Veranschaulichung.
Skizze
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die $x_1$ -Koordinate der Mauer und die $x_1$ -Koordinate der Flugbahn ergeben eine Gleichung mit der Lösung $t_1$ .
Da die Mauer eine Höhe von $3$ Metern hat, kann der Ball die Mauer nur treffen, wenn die $x_3$ -Koordinate der Flugbahn zwischen $0$ und $3$ liegt.