Wahlteil - GTR - lernen mit Serlo!

Aufgabe 3C

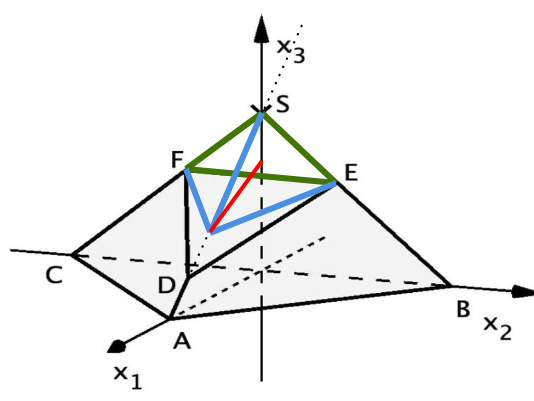
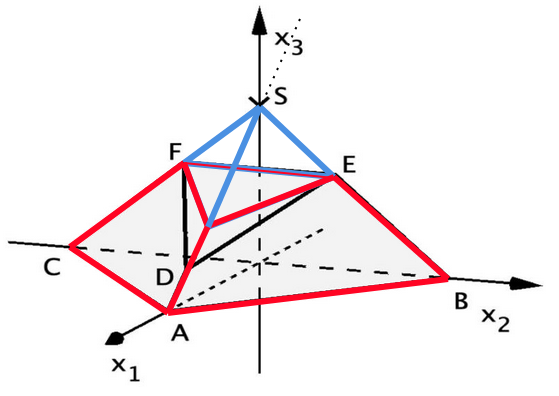
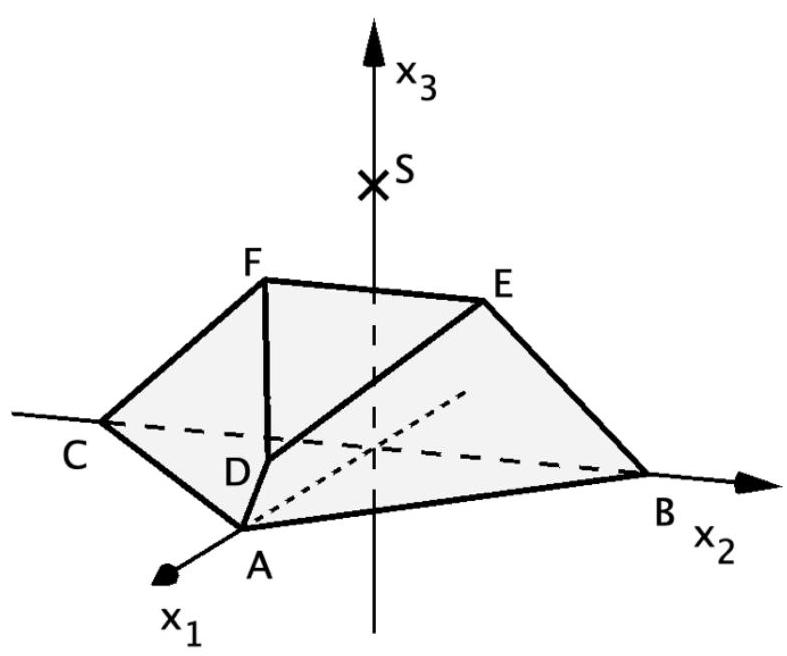
Die Abbildung zeigt den Körper $A B C D E F$ mit $A(10|0| 0), B(0|7{,}5| 0), C(0|-7{,}5| 0), D(8|0| 1),$ $E(0|3| 3)$ und $F(0|-3| 3)$ . Das Dreieck $A B C$ wird als Grundfläche und das Dreieck $D E F$ als Deckfläche des Körpers bezeichnet. Die Deckfläche liegt in der Ebene $L$ .

Zeigen Sie, dass das Dreieck $A B C$ gleichschenklig ist. Berechnen Sie den Innenwinkel des Dreiecks $A B C$ im Eckpunkt $A$ .

Begründen Sie, dass die Kante $\overline{E F}$ parallel zur Grundfläche liegt. (7 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichschenkliges Dreieck

Gleichschenkliges Dreieck

Wir berechnen die Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AC}$ :

$\displaystyle \overrightarrow{AB}$	$=$	$\displaystyle \overrightarrow{OB}-\overrightarrow{OA}=\begin{pmatrix}0-10\\7{,}5-0\\0-0\end{pmatrix}=\begin{pmatrix}-10\\7{,}5\\0\end{pmatrix}$
$\displaystyle \overrightarrow{AC}$	$=$	$\displaystyle \overrightarrow{OC}-\overrightarrow{OA}=\begin{pmatrix}0-10\\-7{,}5-0\\0-0\end{pmatrix}=\begin{pmatrix}-10\\-7{,}5\\0\end{pmatrix}$

Die Einträge in den Vektoren haben die gleichen Beträge, weshalb die Vektoren gleich lang sind. Das Dreieck $ABC$ ist damit gleichschenklig, da zwei Seiten gleich sind.

Winkel im Punkt $A$

Die Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AC}$ haben die Längen:

$|\overrightarrow{AB}|=\sqrt{(-10)^2+7{,}5^2+0^2}=12{,}5=|\overrightarrow{AC}|$

Wir setzen die Vektoren und deren Längen in die Formel für den Winkel zwischen Vektoren ein:

$\displaystyle \cos\alpha$	$=$	$\displaystyle \dfrac{\vec{a}\cdot\vec{b}}{\|\vec{a}\|\cdot\|\vec{b}\|}$
	$=$	$\displaystyle \dfrac{\begin{pmatrix}-10\\7{,}5\\0\end{pmatrix}\cdot \begin{pmatrix}-10\\-7{,}5\\0\end{pmatrix}}{12{,}5\cdot 12{,}5}$
	$=$	$\displaystyle \frac{43{,}75}{156{,}25}$	$\displaystyle \cos^{-1}\left(\right)$
$\displaystyle \alpha$	$≈$	$\displaystyle 74°$

Seite $\overline{E F}$

Der Vektor $\overrightarrow{EF}=\overrightarrow{OF}-\overrightarrow{OE}=\begin{pmatrix}0-0\\-3-3\\3-3\end{pmatrix}=\begin{pmatrix}0\\-6\\0\end{pmatrix}$ verläuft in die Richtung der $x_2$ -Achse, denn die anderen Koordinaten sind 0. Damit ist die Seite $\overline{E F}$ parallel zu dieser Achse.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Der Körper $A B C D E F$ kann zu einer Pyramide mit der Grundfläche $A B C$ und der Spitze $S$ ergänzt werden, wobei $D, E$ und $F$ auf den Kanten der Pyramide liegen.

Begründen Sie, dass $S$ in der $x_{2} x_{3}$ -Ebene liegt. (5 BE)

Berechnen Sie die Koordinaten von $S$ . [Zur Kontrolle: $S(0|0| 5)$ ]

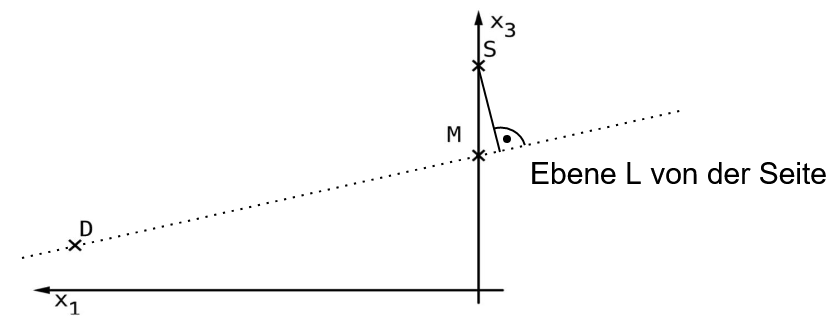
$S$ ist auch Spitze einer Pyramide mit der Grundfläche $D E F$ . Die nebenstehende Abbildung zeigt in der $x_{1} x_{3}$ -Ebene die Punkte $D$ und $S$ sowie den Mittelpunkt $M$ der Kante $\overline{E F}$ .
Begründen Sie, dass der Abstand von $S$ zur Ebene $L$ kleiner als $2$ ist, und veranschaulichen Sie Ihre Begründung durch geeignete Eintragungen in der untenstehenden Abbildung. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lot
Abstand von $S$ zur Ebene $L$
Der Punkt $M$ hat die Koordinaten $(0|0|3)$ , da er die Mitte der Punkte $E(0|3| 3)$ und $F(0|-3| 3)$ ist.
Der Abstand von $M(0|0|3)$ und $S(0|0|5)$ ist $2$ Längeneinheiten.
Den kleinsten Abstand hat $S$ zur Ebene im Lotfußpunkt. Das Lot hat eine kleinere Länge als 2, weshalb der Abstand von $S$ zur Ebene kleiner als 2 ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne den Abstand von $S$ und $M$ . Überlege, wo der kürzeste Abstand von $S$ zur Ebene vorliegt.
Für $t \in[0 ; 1]$ besitzen die Punkte $D_{t}$ der Strecke $\overline{D S}$ die $x_{1}$ -Koordinate $8-8 t$ .
$A_{E F S}$ ist der Flächeninhalt des Dreiecks EFS.
Begründen Sie, dass das Volumen der Pyramide $E F S D_{t}$ mit dem Term $\frac{1}{3} \cdot A_{E F S} \cdot(8-8 t)$ berechnet werden kann.
Beschreiben Sie ein Vorgehen zur Berechnung des Volumens des Körpers $A B C D_{t} E F$ .
(4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Volumen der Pyramide
Die Formel zur Berechnung des Volumens einer dreiseitigen Pyramide lautet:
$V=\frac13 G\cdot h$
Die Grundfläche ist für alle Werte von $t$ gegeben durch $A_{E F S}$ .
Die Höhe verändert sich mit $t$ , wobei die Länge der Höhe gerade der $x_1$ -Koordinate des Vektors $\overrightarrow{DS}$ entspricht.
Eingesetzt ergibt sich also:
$\displaystyle V$ $=$ $\displaystyle \frac13 G\cdot h$
$=$ $\displaystyle \frac13 A_{E F S}\cdot (8-8 t)$
Volumen des Körpers $A B C D_{t} E F$
Das Volumen von $A B C D_{t} E F$ entspricht das Volumen des roten Körpers.
Berechnet man das Volumen der ganzen Pyramide $ABCS$ kann das Volumen der kleinen, blauen Pyramide $EFD_tS$ abgezogen werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Verwende die Formel für das Volumen einer Dreieckspyramide.
Das Volumen des Körpers $A B C D_{t} E F$ kann mithilfe des Volumens von $E F S D_{t}$ berechnet werden.

$\displaystyle V$	$=$	$\displaystyle \frac13 G\cdot h$
	$=$	$\displaystyle \frac13 A_{E F S}\cdot (8-8 t)$

Aufgabe 3C

Gleichschenkliges Dreieck

Winkel im Punkt AAA

Seite EF‾\overline{E F}EF

Hast du eine Frage oder Feedback?

SSS liegt in der x2x_2x2​-x3x_3x3​-Ebene

Koordinaten von SSS

Hast du eine Frage oder Feedback?

Abstand von SSS zur Ebene LLL

Hast du eine Frage oder Feedback?

Volumen der Pyramide

Volumen des Körpers ABCDtEFA B C D_{t} E FABCDt​EF

Hast du eine Frage oder Feedback?

Winkel im Punkt $A$

Seite $\overline{E F}$

$S$ liegt in der $x_2$ - $x_3$ -Ebene

Koordinaten von $S$

Abstand von $S$ zur Ebene $L$

Volumen des Körpers $A B C D_{t} E F$