Pflichtteil - Stochastik - lernen mit Serlo!

Aufgabe P5

Die Zufallsgröße $X$ ist binomialverteilt; die Trefferwahrscheinlichkeit beträgt $p=\frac{1}{4}$ .
Vervollständigen Sie die folgende Gleichung zur Berechnung einer Wahrscheinlichkeit:
$\displaystyle P(X=\quad)=\binom{}{3} \cdot\left(\frac{1}{4}\right)^{3} \cdot(-)^{2}$
. (2BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Term vervollständigen
$P(X=\quad)=\binom{}{3} \cdot\left(\frac{1}{4}\right)^{3} \cdot(-)^{2}$
Die Trefferwahrscheinlichkeit kommt 3 mal vor, es wird also dreimal getroffen.
Die Gegenwahrscheinlichkeit $1-p=\dfrac34$ kommt 2 mal vor, es wird also zweimal nicht getroffen.
Damit ist $n = 5$ . Da dreimal getroffen wird, wird mit diesem Term $P (X = 3)$ berechnet:
$\displaystyle P(X=\color{green}3\color{black})=\binom{\color{green}5}{3} \cdot\left(\frac{1}{4}\right)^{3} \cdot\left(\color{green}\frac{3}{4}\color{black}\right)^{2}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Untersuche den Term darauf, wie oft die Trefferwahrscheinlichkeit vorkommt.
Bestimme zudem, wie oft die Gegenwahrscheinlichkeit vorkommt, um die Anzahl der Durchführungen $n$ zu bestimmen.
Die Abbildung zeigt die symmetrische Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße $Y$ .
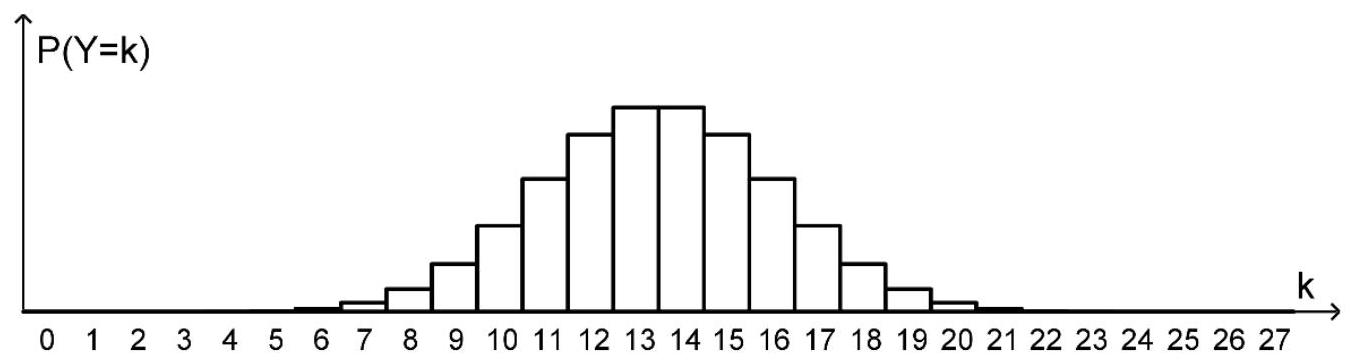
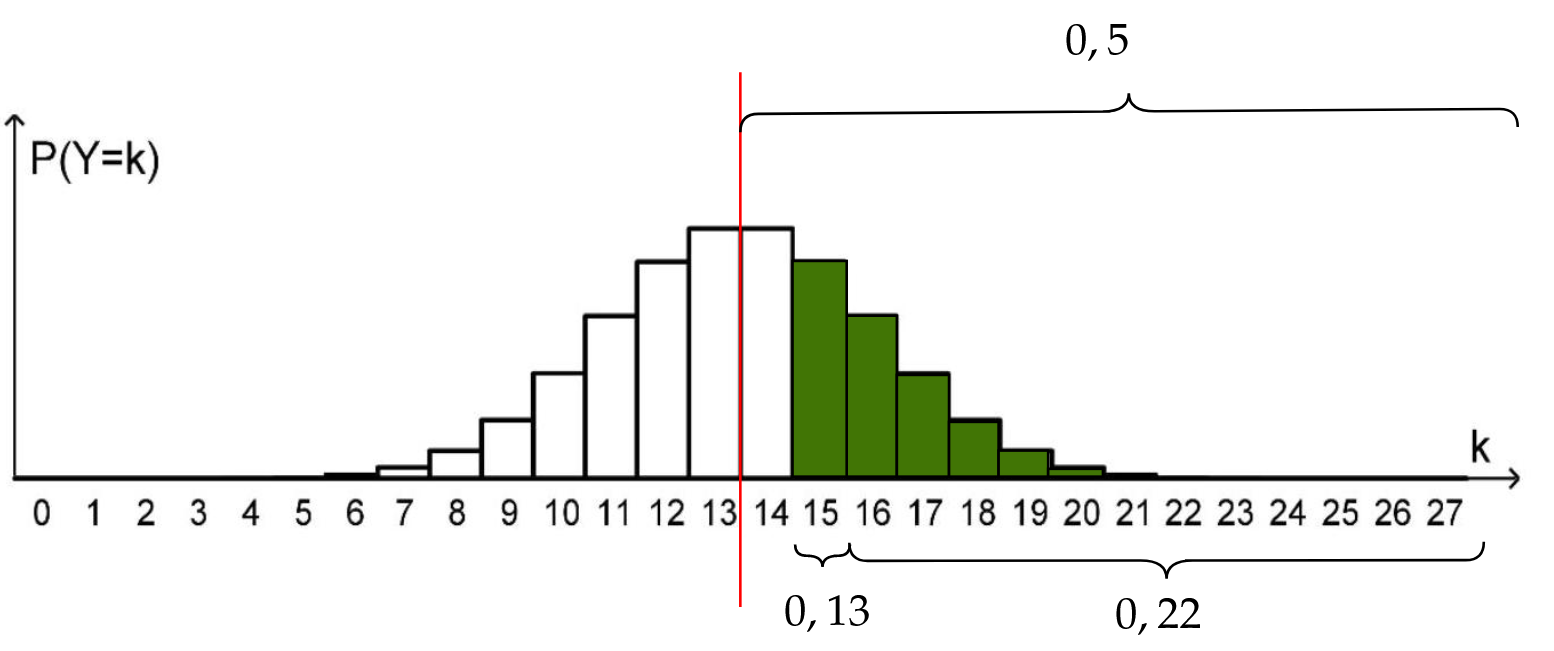
Gegeben sind die Wahrscheinlichkeitswerte $P(Y \leq 15) \approx 0{,}78$ und $P(Y=12) \approx 0{,}13$ .
Berechnen Sie unter Verwendung dieser Werte einen Näherungswert für die
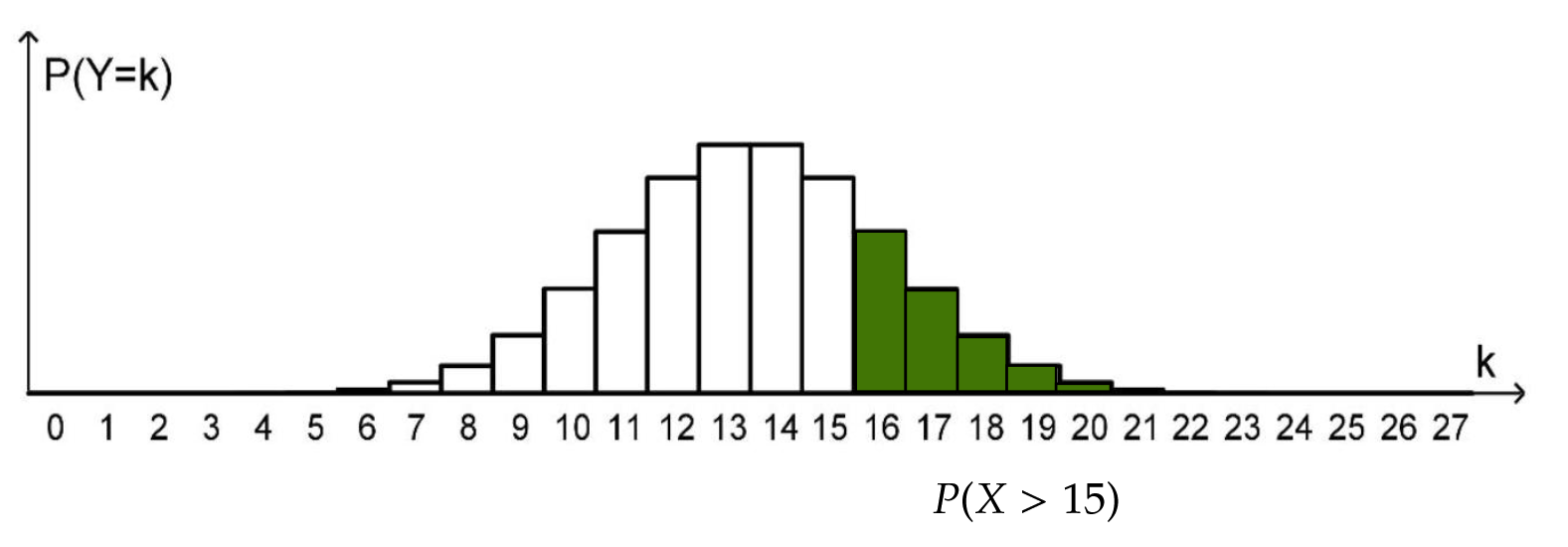
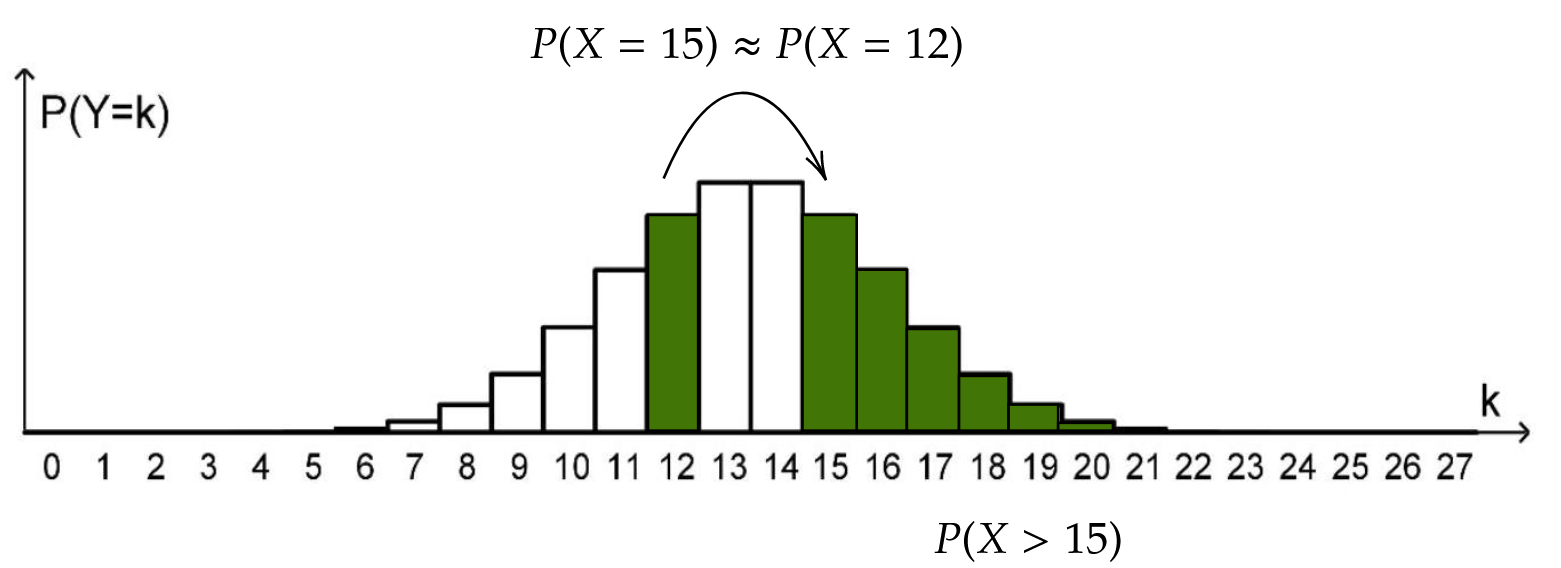
Wahrscheinlichkeit $P (Y = 14)$ . (3BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Wahrscheinlichkeit $P (X = 14)$ bestimmen
Es gilt $P(X\le 15)\approx0{,}78$ .
Damit ist die Gegenwahrscheinlichkeit:
$\displaystyle P(X> 15)\approx0{,}22$
Die Wahrscheinlichkeit $P (X = 12)$ ist wegen der Symmetrie gleich der Wahrscheinlichkeit $P(X=15)\approx 0{,}13$ .
Verwende die Symmetrie, sodass die rechte Seite der Verteilung zusammen die Wahrscheinlichkeit $0,5$ ergeben muss:
Damit ist $P (X = 14) = 0,5 - 0,13 - 0,22 = 0,15$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Verwende, dass die Binomialverteilung näherungsweise symmetrisch um ihre Mitte ist.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgabe P5

Term vervollständigen

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit P(X=14)P(X=14)P(X=14) bestimmen

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit $P (X = 14)$ bestimmen