Teil 2 Analysis I - lernen mit Serlo!

Das Auf- und Abtauchverhalten eines Delfins im Meer wird mittels eines an ihm angebrachten Sensors untersucht. Die momentane Höhe des Sensors in Metern bezogen auf dei Wasseroberfläche in Abhängigkeit von der Zeit t in Sekunden lässt sich annähernd durch die Funktionswerte der Funktion T beschreiben.

Der Graph der Funktion T wird mit $G_{T}$ bezeichnet und ist im Zeitraum von 0 bis 8 Sekunden im nebenstehenden Koordinatensystem abgebildet.

Die Funktion T ist eine ganzrationale Funktion vierten Grades und zum Zeitpunkt $t_{1} = 1$ befindet sich der Delfin an der Wasseroberfläche.

Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.

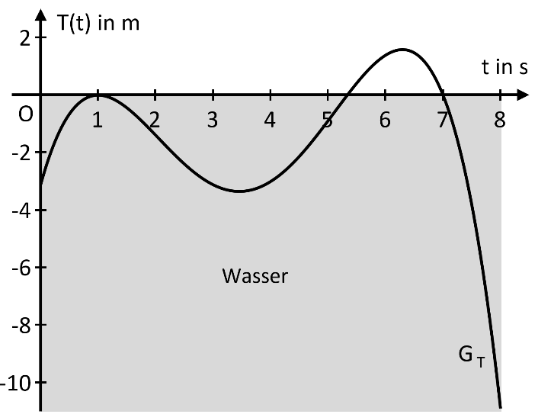
Beschreiben Sie anhand des Funktionsgraphen $G_{T}$ den Bewegungsablauf des Delfins im Bereich von $t \approx 5,3$ bis $t = 7$ und erläutern Sie, ob für die Funktion T das Intervall $[0; \infty [$ für den beschriebenen Sachverhalt eine sinnvolle Definitionsmenge ist. (2 BE)

Verhalten des Delfins für $x \in [5,3; 7]$
Da die x-Achse der Wasseroberfläche entspricht, ist der Delfin für $x \in [5,3; 7]$ über der Wasseroberfläche. Er springt also aus dem Wasser.
Verhalten für $x \to \infty$
Da der Graph zu einer Funktion 4. Grades gehört, deren drei Extremstellen bereits im dargestellten Bereich sind, fällt er immer weiter.
Der Delfin würde also unendlich tief tauchen, was nicht möglich ist, da das Meer nicht unendlich tief ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Lese dir aufmerksam durch, was durch den Graph dargestellt wird und was du über die Funktion weißt.
Der Leitkoeffizient im Funktionsterm von T ist gegeben durch $a = - \frac{1}{12}$ . Zudem ist bekannt, dass $G_{T}$ den Schnittpunkt $S (0 | - \frac{28}{9})$ mit der Ordinatenachse besitzt.
Die zwei ganzzahligen Nullsteleln von T können der Zeichnung entnommen werden.
Berechnen Sie den exakten Wert der fehlenden Nullstelle von T. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linearfaktordarstellung einer Polynomfunktion beliebigen Grades
Funktionsterm aufstellen
Du weißt, dass es sich um eine Funktion 4. Grades handelt, die die doppelte Nullstelle $x = 1$ und die einfache Nullstelle $x = 7$ besitzt (Vielfachheit von Nullstellen).
Aus der Aufgabenstellung weißt du, dass der Leitkoeffizent $a = - \frac{1}{12}$ ist.
Damit ergibt sich der Funktionsterm $T (x) = - \frac{1}{12} (x - 1)^{2} (x - 7) (x - n)$ ,
wobei n die fehlende Nullstelle ist.
Punkt S einsetzen
Setze $S (0 | - \frac{28}{9})$ in den Term ein:
$- \frac{28}{9}$ $=$ $- \frac{1}{12} {(0 - 1)}^{2} (0 - 7) (0 - n)$
↓
Verrechne
$- \frac{28}{9}$ $=$ $- \frac{7}{12} n$ $: (- \frac{7}{12})$
$\frac{16}{3}$ $=$ $n$
Achtung! Da die exakte Lage gefragt ist, darf nicht (direkt) der gerundete Wert 5,33 angegeben werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Verwende die Produktform (Linearfaktorendarstellung), um einen möglichen Funktionsterm aufzustellen.
Nullstellen kannst du dem Graphen entnehmen.
Leitkoeffizient der Aufgabenstellung.
Die unbekannte Nullstelle bezeichnest du mit einem beliebigen Buchstaben.
Bestimme den Wert der Nullstelle, indem du S einsetzt.
Die Funktion T ist gegeben durch die Funktionsgleichung $T (t) = - \frac{1}{12} (t^{4} - \frac{43}{3} t^{3} + 63 t^{2} - 87 t + \frac{112}{3})$ mit der Definitionsmenge $D_{T} = [0; 8]$ .
Runden Sie Ihre Ergebnisse gegebenenfalls auf zwei Nachkommastellen.
Bestimmen Sie die Wertemenge $W_{T}$ der Funktion T und interpretieren Sie diese im Sachzusammenhang. (9 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertemenge
Bestimmung der Extremstellen
Bestimme die erste Ableitung $T^{'} :$
$T^{'} (t) = - \frac{1}{12} (4 t^{3} - 43 t^{2} + 126 t - 87)$
Bestimme die Nullstellen der 1. Ableitung.
$T^{'} (t)$ $=$ $0$
$0$ $=$ $- \frac{1}{12} (4 t^{3} - 43 t^{2} + 126 t - 87)$ $: (- \frac{1}{12})$
$0$ $=$ $4 t^{3} - 43 t^{2} + 126 t - 87$
Du musst eine Polynomdivision ausführen.
Du weißt aus dem Graphen, dass bei $x = 1$ ein Hochpunkt liegt, also wird die Ableitungsfunktion dort eine Nullstelle haben.
Verwende diese für die Polynomdivision:
$\begin{array}{lll} (4 t^{3} - 43 t^{2} + 126 t - 87) & : (t - 1) & = 4 t^{2} - 39 t + 87 \\ - (4 t^{3} - 4 t^{2}) \\ - 39 t^{2} + 126 t \\ - (- 39 t^{2} + 39 t) \\ + 87 t - 87 \\ - (87 t - 87) \\ 0 \end{array}$
Bestimme die Lösungen von $0 = 4 t^{2} - 39 t + 87$ mithilfe der Mitternachtsformel, um die anderen beiden Extremstellen zu bekommen.
$t_{2 / 3} = \frac{- (- 39) \pm \sqrt{(- 39)^{2} - 4 \cdot 4 \cdot 87}}{2 \cdot 4}$ liefert $t_{2} \approx 3,46$ und $t_{3} \approx 6,29$
Da alle drei Nullstellen der Ableitung eine einfache Vielfachheit haben, hat $G_{T}$ drei Extremstellen (wie im Graph bereits zu sehen).
Die Art der Extremstellen ist nicht gefragt, deshalb kannst du direkt die Lage der relevanten Extremstellen bestimmen.
Lage der relevanten Extremstellen
Da du den Graph gegeben hast, siehst du bereits, dass bei $t = 8$ der absolute Tiefpunkt liegen wird und bei $t \approx 6,29$ der absolute Hochpunkt.
Setze diese Werte in T ein:
$T (8) = - \frac{98}{9} \approx - 10,89$ und $T (6,29) \approx 1,58$
Damit ergibt sich die Wertemenge $W = [- 10,89; 1,58]$
Interpretation im Sachkontext
Der Delfin erreicht im Zeitraum von 0 bis 8 Sekunden eine maximale Tiefe von $10,89 m$ unter der Wasseroberfläche und eine maximale Sprunghöhe von $1,58 m$ über der Wasseroberfläche.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Beachte, dass du einen Graph gegeben hast. Dadurch ersparst du dir unnötige Rechnungen.
Um die Wertemenge anzugeben, musst du folgende Schritte ausführen:
Bestimme die Lage der relevanten Extrema
Bestimme die "normalen" Extrema mithilfe der ersten Ableitung
Beachte auch die Randextrema (beide Ränder sind eingeschlossen, deshalb gibt es zwei Randextrema)
Setze nur die Stellen ein, bei denen du im Graph erkennen kannst, dass ein globaler Hoch- oder Tiefpunkt vorliegt und gib die Wertemenge an.
Vergiss nicht, die Wertemenge im Sachzusammenhang zu interpretieren: Was bedeutet die Wertemenge für den Delfin?
Für $t \in] 1; 5,3 [$ befindet sich der Delfin unter Wasser. Ermitteln Sie rechnerisch, ob in diesem Zeitintervall der Betrag der größten Abtauchgeschwindigkeit größer als der Betrag der größten Auftauchgeschwindigkeit ist. (6 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Der Graph hat eine Stelle lokal stärkster Abnahme, wenn der Graph der Ableitungsfunktion $G_{T^{'}}$ einen Tiefpunkt unter der x-Achse besitzt.
Analog gibt es eine Stelle lokal stärkster Zunahme, wenn der Graph der Ableitungsfunktion $G_{T^{'}}$ einen Hochpunkt über der x-Achse besitzt.
Extremstellen der 1. Ableitung
Bestimme die 2. Ableitung von $T^{'} (t) = - \frac{1}{12} (4 t^{3} - 43 t^{2} + 126 t - 87)$ :
$T^{''} (t) = - \frac{1}{12} (12 t^{2} - 86 t + 126)$
Bestimme die Nullstellen von $T^{''}$ :
$T^{''} (t)$ $=$ $0$
$- \frac{1}{12} (12 t^{2} - 86 t + 126)$ $=$ $0$ $: (- \frac{1}{12})$
$12 t^{2} - 86 t + 126$ $=$ $0$
Bestimme die Lösungen mit der Mitternachtsformel:
$t_{1 / 2} = \frac{- (- 86) \pm \sqrt{(- 86)^{2} - 4 \cdot 12 \cdot 126}}{2 \cdot 12}$
Du erhältst die Lösungen $t_{1} \approx 2,05$ und $t_{2} \approx 5,11$
Entscheidung, ob Zu- oder Abnahme
Betrachte das Monotonieverhalten des Graphen $G_{T^{'}}$ der Ableitungsfunktion:
t
0<t<
t=2,05
<t<
t=5,11
<t
Vorzeichen $T^{''}$
$-$
$0$
$+$
$0$
$-$
Verlauf $G_{T^{'}}$
$↘$
TIP
$↗$
HOP
$↘$
Verhalten $G_{T}$
Kandidat für stärkste Abnahme
Kandidat für stärkste Zunahme
Abtauchgeschwindigkeit und Auftauchgeschwindigkeit
Setze $t = 2,05$ und $t = 5,11$ in die erste Ableitung ein. Dadurch beweist du nicht nur, dass es sich tatsächlich um die Stellen stärkster Zu- oder Abnahme handelt, du bestimmst auch die gesuchten Abtauch- und Auftauchgeschwindigkeiten.
$T^{'} (2,05) \approx - 2,09$ ( $G_{T^{'}}$ hat TIP unter x-Achse)
$T^{'} (5,11) \approx 2,69$ ( $G_{T^{'}}$ hat HOP über der x-Achse)
Die größte Auftauchgeschwindigkeit ist mit $2,69 \frac{m}{s}$ größer als die größte Abtauchgeschwindigkeit von $2,09 \frac{m}{s}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Gesucht sind die Stellen, in denen der Delfin am schnellsten abtaucht bzw. auftaucht.
Das sind die Stellen lokal stärkster Ab- oder Zunahme.
Du suchst also die Extremstellen der 1. Ableitung.

t	0<t<	t=2,05	<t<	t=5,11	<t
Vorzeichen $T^{''}$	$-$	$0$	$+$	$0$	$-$
Verlauf $G_{T^{'}}$	$↘$	TIP	$↗$	HOP	$↘$
Verhalten $G_{T}$		Kandidat für stärkste Abnahme		Kandidat für stärkste Zunahme

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

$- \frac{28}{9}$	$=$	$- \frac{1}{12} {(0 - 1)}^{2} (0 - 7) (0 - n)$
	↓	Verrechne
$- \frac{28}{9}$	$=$	$- \frac{7}{12} n$	$: (- \frac{7}{12})$
$\frac{16}{3}$	$=$	$n$

$T^{'} (t)$	$=$	$0$
$0$	$=$	$- \frac{1}{12} (4 t^{3} - 43 t^{2} + 126 t - 87)$	$: (- \frac{1}{12})$
$0$	$=$	$4 t^{3} - 43 t^{2} + 126 t - 87$

$T^{''} (t)$	$=$	$0$
$- \frac{1}{12} (12 t^{2} - 86 t + 126)$	$=$	$0$	$: (- \frac{1}{12})$
$12 t^{2} - 86 t + 126$	$=$	$0$

Verhalten des Delfins für x∈[5,3;7]

Verhalten für x→∞

Hast du eine Frage oder Feedback?

Funktionsterm aufstellen

Punkt S einsetzen

Hast du eine Frage oder Feedback?

Bestimmung der Extremstellen

Lage der relevanten Extremstellen

Interpretation im Sachkontext

Hast du eine Frage oder Feedback?

Extremstellen der 1. Ableitung

Entscheidung, ob Zu- oder Abnahme

Abtauchgeschwindigkeit und Auftauchgeschwindigkeit

Hast du eine Frage oder Feedback?

Verhalten des Delfins für $x \in [5,3; 7]$

Verhalten für $x \to \infty$