Teil 2 Analysis I

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgaben zum Ausdrucken als PDF findest du hier.

Bei der Bearbeitung der Aufgaben dürfen Hilfsmittel verwendet werden

Das Auf- und Abtauchverhalten eines Delfins im Meer wird mittels eines an ihm angebrachten Sensors untersucht. Die momentane Höhe des Sensors in Metern bezogen auf dei Wasseroberfläche in Abhängigkeit von der Zeit t in Sekunden lässt sich annähernd durch die Funktionswerte der Funktion T beschreiben.

Der Graph der Funktion T wird mit $G_T$ bezeichnet und ist im Zeitraum von 0 bis 8 Sekunden im nebenstehenden Koordinatensystem abgebildet.

Die Funktion T ist eine ganzrationale Funktion vierten Grades und zum Zeitpunkt $t_1=1$ befindet sich der Delfin an der Wasseroberfläche.

Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.

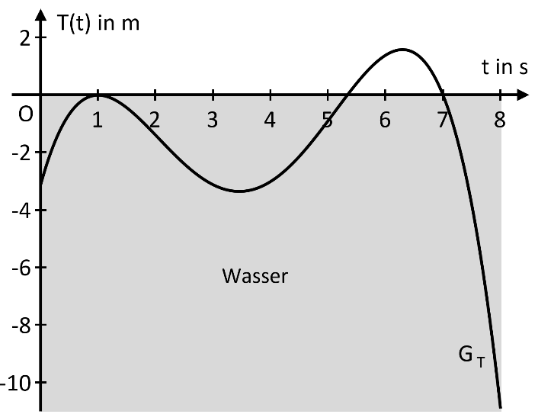
Beschreiben Sie anhand des Funktionsgraphen $G_T$ den Bewegungsablauf des Delfins im Bereich von $t\approx 5{,}3$ bis $t=7$ und erläutern Sie, ob für die Funktion T das Intervall $[0;\infty[$ für den beschriebenen Sachverhalt eine sinnvolle Definitionsmenge ist. (2 BE)

Verhalten des Delfins für $x\in [5{,}3;7]$
Da die x-Achse der Wasseroberfläche entspricht, ist der Delfin für $x\in[5{,}3;7]$ über der Wasseroberfläche. Er springt also aus dem Wasser.
Verhalten für $x\to\infty$
Da der Graph zu einer Funktion 4. Grades gehört, deren drei Extremstellen bereits im dargestellten Bereich sind, fällt er immer weiter.
Der Delfin würde also unendlich tief tauchen, was nicht möglich ist, da das Meer nicht unendlich tief ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Lese dir aufmerksam durch, was durch den Graph dargestellt wird und was du über die Funktion weißt.

Der Leitkoeffizient im Funktionsterm von T ist gegeben durch $a=-\frac 1{12}$ . Zudem ist bekannt, dass $G_T$ den Schnittpunkt $S(0|-\frac{28}9)$ mit der Ordinatenachse besitzt.

Die zwei ganzzahligen Nullsteleln von T können der Zeichnung entnommen werden.

Berechnen Sie den exakten Wert der fehlenden Nullstelle von T. (4 BE)

Die Funktion T ist gegeben durch die Funktionsgleichung $T(t)=-\frac 1{12}(t^4-\frac{43}3t^3+63t^2-87t+\frac{112}3)$ mit der Definitionsmenge $D_T=[0;8]$ .

Runden Sie Ihre Ergebnisse gegebenenfalls auf zwei Nachkommastellen.

Bestimmen Sie die Wertemenge $W_T$ der Funktion T und interpretieren Sie diese im Sachzusammenhang. (9 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertemenge

Bestimmung der Extremstellen

Bestimme die erste Ableitung $T':$

$T'(t)=-\frac 1 {12}(4t^3-43t^2+126t-87)$

Bestimme die Nullstellen der 1. Ableitung.

$\displaystyle T'\left(t\right)$	$=$	$\displaystyle 0$
$\displaystyle 0$	$=$	$\displaystyle -\frac{1}{12}\left(4t^3-43t^2+126t-87\right)$	$\displaystyle :\left(-\frac{1}{12}\right)$
$\displaystyle 0$	$=$	$\displaystyle 4t^3-43t^2+126t-87$

Du musst eine Polynomdivision ausführen.

Du weißt aus dem Graphen, dass bei $x=1$ ein Hochpunkt liegt, also wird die Ableitungsfunktion dort eine Nullstelle haben.

Verwende diese für die Polynomdivision:

$\def\arraystretch{1.25} \begin{array}{lll} \phantom{-}(4t^3-43t^2+126t-87)&:(t-1)&=4t^2-39t+87\\ \underline{-(4t^3-4t^2)}\\ \phantom{-(4t^3}-39t^2+126t\\ \phantom{-(4t}\underline{-(-39t^2+39t)}\\ \phantom{-(4t^3-39t^2)}+87t-87\\ \phantom{-(4t^3-39t^2)}\underline{-(87t-87)}\\ \phantom{-(4x^3-39x^2xxxxxxx)}0 \end{array}$

Bestimme die Lösungen von $0=4t^2-39t+87$ mithilfe der Mitternachtsformel, um die anderen beiden Extremstellen zu bekommen.

$t_{2/3}=\frac{-(-39)\pm\sqrt{(-39)^2-4\cdot4\cdot 87}}{2\cdot 4}$ liefert $t_2\approx3{,}46$ und $t_3\approx6{,}29$

Da alle drei Nullstellen der Ableitung eine einfache Vielfachheit haben, hat $G_T$ drei Extremstellen (wie im Graph bereits zu sehen).

Die Art der Extremstellen ist nicht gefragt, deshalb kannst du direkt die Lage der relevanten Extremstellen bestimmen.

Lage der relevanten Extremstellen

Da du den Graph gegeben hast, siehst du bereits, dass bei $t=8$ der absolute Tiefpunkt liegen wird und bei $t\approx 6{,}29$ der absolute Hochpunkt.

Setze diese Werte in T ein:

$T(8)=-\frac{98}9\approx -10{,}89$ und $T(6{,}29)\approx1{,}58$

Damit ergibt sich die Wertemenge $W=[-10{,}89;1{,}58]$

Interpretation im Sachkontext

Der Delfin erreicht im Zeitraum von 0 bis 8 Sekunden eine maximale Tiefe von $10{,}89 m$ unter der Wasseroberfläche und eine maximale Sprunghöhe von $1{,}58m$ über der Wasseroberfläche.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Für $t\in]1;5{,}3[$ befindet sich der Delfin unter Wasser. Ermitteln Sie rechnerisch, ob in diesem Zeitintervall der Betrag der größten Abtauchgeschwindigkeit größer als der Betrag der größten Auftauchgeschwindigkeit ist. (6 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen

Der Graph hat eine Stelle lokal stärkster Abnahme, wenn der Graph der Ableitungsfunktion $G_{T'}$ einen Tiefpunkt unter der x-Achse besitzt.

Analog gibt es eine Stelle lokal stärkster Zunahme, wenn der Graph der Ableitungsfunktion $G_{T'}$ einen Hochpunkt über der x-Achse besitzt.

Extremstellen der 1. Ableitung

Bestimme die 2. Ableitung von $T'(t)=-\frac 1{12}(4t^3-43t^2+126t-87)$ :

$T''(t)=-\frac 1{12}(12t^2-86t+126)$

Bestimme die Nullstellen von $T''$ :

$\displaystyle T''\left(t\right)$	$=$	$\displaystyle 0$
$\displaystyle -\frac{1}{12}\left(12t^2-86t+126\right)$	$=$	$\displaystyle 0$	$\displaystyle :\left(-\frac{1}{12}\right)$
$\displaystyle 12t^2-86t+126$	$=$	$\displaystyle 0$

Bestimme die Lösungen mit der Mitternachtsformel:

$t_{1/2}=\frac{-(-86)\pm\sqrt{(-86)^2-4\cdot 12\cdot 126}}{2\cdot12}$

Du erhältst die Lösungen $t_1\approx 2{,}05$ und $t_2\approx 5{,}11$

Entscheidung, ob Zu- oder Abnahme

Betrachte das Monotonieverhalten des Graphen $G_{T'}$ der Ableitungsfunktion:

t	0<t<	t=2,05	<t<	t=5,11	<t
Vorzeichen $T''$	$-$	$0$	$+$	$0$	$-$
Verlauf $G_{T'}$	$\searrow$	TIP	$\nearrow$	HOP	$\searrow$
Verhalten $G_T$		Kandidat für stärkste Abnahme		Kandidat für stärkste Zunahme

Abtauchgeschwindigkeit und Auftauchgeschwindigkeit

Setze $t=2{,}05$ und $t=5{,}11$ in die erste Ableitung ein. Dadurch beweist du nicht nur, dass es sich tatsächlich um die Stellen stärkster Zu- oder Abnahme handelt, du bestimmst auch die gesuchten Abtauch- und Auftauchgeschwindigkeiten.

$T'(2{,}05)\approx-2{,}09$ ( $G_{T'}$ hat TIP unter x-Achse)

$T'(5{,}11)\approx 2{,}69$ ( $G_{T'}$ hat HOP über der x-Achse)

Die größte Auftauchgeschwindigkeit ist mit $2{,}69 \frac{m}{s}$ größer als die größte Abtauchgeschwindigkeit von $2{,}09\frac m s$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

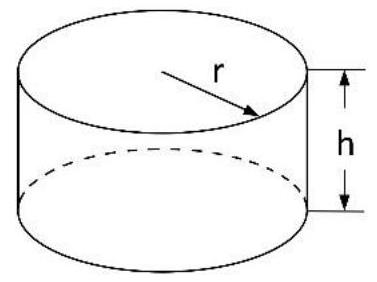
An einem Küstenabschnitt stranden immer wieder Delfine. Diese werden in einer Auffangstation gesund gepflegt, bis sie wieder in freier Natur überleben können. Um die Kapazität der Auffangstation zu erhöhen, soll ein zusätzliches Becken aus Edelstahl angefertigt werden, welches die Form eines geraden Kreiszylinders hat und nach oben offen ist.

Dazu steht ein begrenzter Vorrat an Edelstahlblechen zur Verfügung. Diese haben modellhaft insgesamt eine Fläche von $180 \pi \mathrm{m}^{2}$ . Aus Platzgründen kann das Becken nur einen maximalen Durchmesser von $20 \mathrm{~m}$ haben.

Die Funktion $V: r \mapsto V(r)$ beschreibt die Maßzahl des Volumens des Beckens in Kubikmetern in Abhängigkeit vom Radius $r$ in Metern.

Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden. Runden Sie Ihre Ergebnisse gegebenenfalls auf eine Nachkommastelle.

Stellen Sie eine Gleichung der Funktion V auf. Begründen Sie, dass für die mathematisch maximale Definitionsmenge der Funktion $V$ gilt: $\left.D_{V}=\right] 0 ; 10$ ]

[ Mögliches Ergebnis: $V(r)=-\frac{1}{2} \pi r^{3}+90 \pi r$ ] (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe

Haupt- und Nebenbedingung

Es handelt sich um ein Aquarium in Form eines Zylinders, dessen maximales Volumen später gesucht ist. Deshalb ist unsere Hauptbedingung, die von der Höhe h und dem Radius r abhängig ist:

$V(h,r)=r^2\pi h$

Die Nebenbedingung kannst du aus dem Text herauslesen: Das Aquarium ist nach oben geöffnet und besteht aus $180\pi \mathrm{m}^2$ .

Der Oberflächeninhalt A ist gegeben
	↓
$\displaystyle A$	$=$	$\displaystyle 180\pi$
$\displaystyle Boden+Mantel$	$=$	$\displaystyle 180\pi$
	↓	Der Mantel ist ein Rechteck mit den Seitenlängen $2\pi r$ und h, wobei $2\pi r$ dem Umfang des Kreises entspricht.
$\displaystyle r^2\ \pi+2\pi r\cdot h$	$=$	$\displaystyle 180\pi$

Nebenbedingung umformen und in Hauptbedingung einsetzen

In deiner Hauptbedingung soll nur noch die Variable r vorkommen. Forme deswegen die Nebenbedingung nach h um:

$\displaystyle r^2\pi\ +\ 2\pi rh$	$=$	$\displaystyle 180\pi$	$\displaystyle -r^2\pi$
$\displaystyle 2\pi rh$	$=$	$\displaystyle 180\pi-r^2\pi$	$\displaystyle :2\pi r$
$\displaystyle h$	$=$	$\displaystyle \frac{180\pi-r^2\pi}{2\pi r}$
	↓	Setze h in die Hauptbedingung ein
$\displaystyle V\left(r\right)$	$=$	$\displaystyle r^2\pi\cdot\frac{180\pi-r^2\pi}{2\pi r}$
$\displaystyle V(r)$	$=$	$\displaystyle \frac{r^{\not2}\not{\pi}\cdot\left(180\pi-r^2\pi\right)}{2\not{\pi} \not r}$
	↓	Kürze
$\displaystyle V(r)$	$=$	$\displaystyle 90\pi r-0{,}5r^3$

Untersuchung der Definitionsmenge

untere Grenze: Die Zahl 0 ist aus der Definitionsmenge ausgeschlossen, da der Radius nicht negativ sein kann und auch für den Radius 0 noch kein Aquarium entsteht.

obere Grenze: Laut Vorgabe in der Aufgabenstellung soll der Durchmesser maximal 20m betragen. Der Radius ist der halbe Durchmesser, also 10m.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Zeigen Sie, dass unter den oben genannten Vorgaben das Becken für einen Radius von $r=2 \sqrt{15}$ den maximalen Rauminhalt aufweist. Überprüfen Sie anschließend, ob dieses Becken für eine vorübergehende Haltung von drei Delfinen ausreicht, wenn pro Delfin $360 \mathrm{~m}^{3}$ Wasser zur Verfügung stehen sollen.

(7 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen

Ableitung von V

Die Ableitung von $V(r)=-\frac 1 2 \pi r^3+90\pi r$ ist:

$V'(r)=-1{,}5\pi r^2+90\pi$

Kandidaten für Extremstellen

Die Kandidaten für Extremstellen von $V$ liegen bei den Nullstellen von $V'$ :

$\displaystyle 0$	$=$	$\displaystyle V'(r)$
$\displaystyle 0$	$=$	$\displaystyle -1{,}5\pi r^2+90\pi$
	↓	$-1{,}5\pi$ ausklammern
$\displaystyle 0$	$=$	$\displaystyle -1{,}5\pi\left(r^2-60\right)$	$\displaystyle :\left(-1{,}5\pi\right)$
$\displaystyle 0$	$=$	$\displaystyle r^2-60$	$\displaystyle +60$
$\displaystyle 60$	$=$	$\displaystyle r^2$
	↓	Ziehe die Wurzel, beachte, dass es zwei Lösungen gibt
$\displaystyle r$	$=$	$\displaystyle \pm\sqrt{60}$
	↓	Zeige, dass $\sqrt{60}=2\sqrt{15}$
$\displaystyle r$	$=$	$\displaystyle \pm\sqrt{4\cdot15}$
	↓	Teilweise radizieren
$\displaystyle r$	$=$	$\displaystyle \pm2\sqrt{15}$

Die Lösung $r=-2\sqrt{15}$ ist negativ und liegt somit nicht in $D_V$ .

Die Lösung $r=2\sqrt{15}\approx7{,}7$ liegt in $D_V=]0;10]$

(Da die Nullstelle eine einfache Vielfachheit hat und es somit eine Nullstelle mit Vorzeichenwechsel ist, liegt dort auch tatsächlich eine Extremstelle)

Funktionswerte an den Extrema und Rändern

Setze die Extremstelle $r=2\sqrt{15}\approx7{,}7$ und die Randextremstelle $r=10$ in $V(r)$ ein:

$V(2\sqrt{15})\approx1460{,}1$

$V(10)\approx1256{,}6$

Da der linke Rand ausgeschlossen ist, musst du hier den Grenzwert von $V(r)$ für $r\to0$ bestimmen:

$lim_{r\to 0}V(r)=0$

Das maximale Volumen gibt es also bei einem Radius von $7{,}7$ m. Es beträgt $1460{,}1 m^3$ .

Artgerechte Delfinhaltung

Drei Delfine brauchen laut Angabe ein Becken, dass mindestens $3\cdot360m^3=1080m^3$ groß ist.

Damit ist das Becken mit $1460{,}1m^3$ ausreichend groß.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Berechnen Sie für den unter 2.2 gegebenen Beckenradius die Größe der Grundfläche des Beckens $A_{0}$ in Quadratmetern.
[ Ergebnis: $A_{0} \approx 188{,}5 \mathrm{~m}^{2}$ ]
(2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisumfang und Kreisfläche
Setze $r=2\sqrt{15}$ in die Formel $A=r^2\pi$ ein:
$A=(2\sqrt{15})^2\pi=60\pi\approx 188{,}5$
Das größtmögliche Becken hat eine Grundfläche von $188{,}5m^2$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Verwende die Formel für den Flächeninhalt des Kreises. Den Radius bekommst du aus der letzten Teilaufgabe.
Ein zu Beginn (Zeitpunkt $t_{0}=0$ ) $0{,}5 \mathrm{~m}^{2}$ großer Algenteppich, der sich am Boden des Beckens mit der Grundfläche $A_{0}$ (siehe 2.3) gebildet hat, verdoppelt seine Fläche täglich.
Stellen Sie eine Gleichung der Funktion $A: t \mapsto A(t)$ auf, welche die Fläche des Algenteppichs in Quadratmetern in Abhängigkeit von der Zeit $t$ in Tagen angibt. Für die Definitionsmenge der Funktion $A$ gilt $D_{A}=[0 ; 8]$ .
(2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Verwende eine einfache Exponentialfunktion der Form $A(t)=a\cdot b^t$
Zu Beginn ist der Algenteppich $0{,}5m^2$ groß: $a=0{,}5$
Die Größe verdoppelt sich täglich: $b=2$
Insgesamt also: $A(t)=0{,}5\cdot 2^t$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es handelt sich um eine Exponentialfunktion
Überlege dir den Startwert
Überlege dir den Wachstumsfaktor

Zeigen Sie, dass sich die Wachstumsfunktion A näherungsweise durch die Funktionsgleichung $\tilde{A}(t)=0{,}5 \cdot e^{0{,}6931 \cdot t}$ mit $D_{\tilde{A}}=D_{A}$ darstellen lässt und berechnen Sie damit, nach wie vielen Tagen zwei Drittel der gesamten Grundfläche des Beckens von Algen bedeckt wären, wenn nicht eingegriffen würde.

Runden Sie Ihr Ergebnis auf ganze Tage.

(6 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle -\frac{28}{9}$	$=$	$\displaystyle -\frac{1}{12}\left(0-1\right)^2\left(0-7\right)\left(0-n\right)$
	↓	Verrechne
$\displaystyle -\frac{28}{9}$	$=$	$\displaystyle -\frac{7}{12}n$	$\displaystyle :\left(-\frac{7}{12}\right)$
$\displaystyle \frac{16}{3}$	$=$	$\displaystyle n$

$\displaystyle \tilde{A}\left(t\right)$	$=$	$\displaystyle 0{,}5\cdot e^{0{,}6931t}$
	↓	Potenzgesetz $a^{x\cdot y}=(a^x)^y$
	$=$	$\displaystyle 0{,}5\cdot\left(e^{0{,}6931}\right)^t$
	↓	Berechne die Potenz in der Klammer: $e^{0{,}6931}\approx1{,}99991\approx2$
	$=$	$\displaystyle 0{,}5\cdot2^t$
	$=$	$\displaystyle A\left(t\right)$

$\displaystyle \tilde{A}\left(t\right)$	$=$	$\displaystyle 40\pi$
$\displaystyle 0{,}5\cdot e^{0{,}6931t}$	$=$	$\displaystyle 40\pi$	$\displaystyle \cdot2$
$\displaystyle e^{0{,}6931t}$	$=$	$\displaystyle 80\pi$
	↓	Verwende den ln
$\displaystyle 0{,}6931t$	$=$	$\displaystyle \ln\left(80\pi\right)$	$\displaystyle :0{,}6931$
$\displaystyle t$	$≈$	$\displaystyle 8{,}0$

Teil 2 Analysis I

Verhalten des Delfins für $x\in [5{,}3;7]$

Verhalten für $x\to\infty$

Hast du eine Frage oder Feedback?

Funktionsterm aufstellen

Punkt S einsetzen

Hast du eine Frage oder Feedback?

Bestimmung der Extremstellen

Lage der relevanten Extremstellen

Interpretation im Sachkontext

Hast du eine Frage oder Feedback?

Extremstellen der 1. Ableitung

Entscheidung, ob Zu- oder Abnahme

Abtauchgeschwindigkeit und Auftauchgeschwindigkeit

Hast du eine Frage oder Feedback?

Haupt- und Nebenbedingung

Nebenbedingung umformen und in Hauptbedingung einsetzen

Untersuchung der Definitionsmenge

Hast du eine Frage oder Feedback?

Ableitung von V

Kandidaten für Extremstellen

Funktionswerte an den Extrema und Rändern

Artgerechte Delfinhaltung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Äquivalenz der Funktionsterme

Bewachsene Beckenfläche

Zeitpunkt berechnen

Hast du eine Frage oder Feedback?

Teil 2 Analysis I

Verhalten des Delfins für x∈[5,3;7]x\in [5{,}3;7]x∈[5,3;7]

Verhalten für x→∞x\to\inftyx→∞

Hast du eine Frage oder Feedback?

Funktionsterm aufstellen

Punkt S einsetzen

Hast du eine Frage oder Feedback?

Bestimmung der Extremstellen

Lage der relevanten Extremstellen

Interpretation im Sachkontext

Hast du eine Frage oder Feedback?

Extremstellen der 1. Ableitung

Entscheidung, ob Zu- oder Abnahme

Abtauchgeschwindigkeit und Auftauchgeschwindigkeit

Hast du eine Frage oder Feedback?

Haupt- und Nebenbedingung

Nebenbedingung umformen und in Hauptbedingung einsetzen

Untersuchung der Definitionsmenge

Hast du eine Frage oder Feedback?

Ableitung von V

Kandidaten für Extremstellen

Funktionswerte an den Extrema und Rändern

Artgerechte Delfinhaltung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Äquivalenz der Funktionsterme

Bewachsene Beckenfläche

Zeitpunkt berechnen

Hast du eine Frage oder Feedback?

Verhalten des Delfins für $x\in [5{,}3;7]$

Verhalten für $x\to\infty$