An einem Küstenabschnitt stranden immer wieder Delfine. Diese werden in einer Auffangstation gesund gepflegt, bis sie wieder in freier Natur überleben können. Um die Kapazität der Auffangstation zu erhöhen, soll ein zusätzliches Becken aus Edelstahl angefertigt werden, welches die Form eines geraden Kreiszylinders hat und nach oben offen ist.
Dazu steht ein begrenzter Vorrat an Edelstahlblechen zur Verfügung. Diese haben modellhaft insgesamt eine Fläche von . Aus Platzgründen kann das Becken nur einen maximalen Durchmesser von haben.
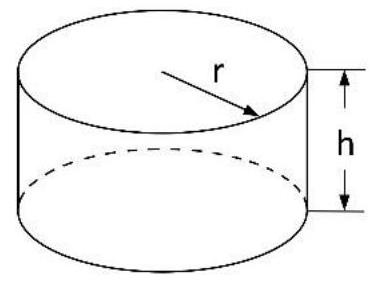
Die Funktion beschreibt die Maßzahl des Volumens des Beckens in Kubikmetern in Abhängigkeit vom Radius in Metern.
Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden. Runden Sie Ihre Ergebnisse gegebenenfalls auf eine Nachkommastelle.
Stellen Sie eine Gleichung der Funktion V auf. Begründen Sie, dass für die mathematisch maximale Definitionsmenge der Funktion gilt: ]
[ Mögliches Ergebnis: ] (5 BE)
Zeigen Sie, dass unter den oben genannten Vorgaben das Becken für einen Radius von den maximalen Rauminhalt aufweist. Überprüfen Sie anschließend, ob dieses Becken für eine vorübergehende Haltung von drei Delfinen ausreicht, wenn pro Delfin Wasser zur Verfügung stehen sollen.
(7 BE)
Berechnen Sie für den unter b) gegebenen Beckenradius die Größe der Grundfläche des Beckens in Quadratmetern.
[ Ergebnis: ]
(2 BE)
Ein zu Beginn (Zeitpunkt ) großer Algenteppich, der sich am Boden des Beckens mit der Grundfläche (siehe c)) gebildet hat, verdoppelt seine Fläche täglich.
Stellen Sie eine Gleichung der Funktion auf, welche die Fläche des Algenteppichs in Quadratmetern in Abhängigkeit von der Zeit in Tagen angibt. Für die Definitionsmenge der Funktion gilt .
(2 BE)
Zeigen Sie, dass sich die Wachstumsfunktion A näherungsweise durch die Funktionsgleichung mit darstellen lässt und berechnen Sie damit, nach wie vielen Tagen zwei Drittel der gesamten Grundfläche des Beckens von Algen bedeckt wären, wenn nicht eingegriffen würde.
Runden Sie Ihr Ergebnis auf ganze Tage.
(6 BE)
