Teil 2 Analysis 2 - lernen mit Serlo!

Der Graph der Funktion $f$ mit der Definitionsmenge $D_{f}=\R$ schneidet in einem kartesischen Koordinatensystem die $y$ -Achse beim Wert $y=2$ und verläuft durch den Extrempunkt $\mathrm{E}(2 \mid 1{,}2)$ . Außerdem ist bekannt, dass der Funktionsterm durch $f(x)=a x^{3}+b x^{2}-0{,}9 x+c$ mit $a, b, c \in I R$ und $a \neq 0$ dargestellt werden kann.

Bestimmen Sie im Funktionsterm von $\mathrm{f}$ die Werte der Parameter $\mathrm{a}, \mathrm{b}$ und $\mathrm{c}$ . (6 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steckbriefaufgaben

Aufstellen der Bedingungsgleichungen

Die Funktion $f(x)=ax^3+bx^2-0{,}9x+c$ hat die Ableitung:

$f'(x)=3ax^2+2bx-0{,}9$

Verwende das für die Bedingungsgleichungen:

"schneidet die y-Achse beim Wert $y=2$ " bedeutet, dass $f(0)=2$
"verläuft durch den Extrempunkt E(2|1,2)" bedeutet:
- $f(2)=1{,}2$
- $f'(2)=0$

Übersetzen in ein Gleichungssystem

Daraus erhältst du die drei Gleichungen

$I) 2=a\cdot 0^3+b\cdot 0^2-0{,}9\cdot 0+c\\ II) 1{,}2=a\cdot 2^3+b\cdot 2^2-0{,}9\cdot 2+c\\ III)0=3a\cdot 2^2+2b\cdot 2 - 0{,}9$

Aus Gleichung I) erhältst du direkt $I)2=c$

Setze c in die anderen beiden Gleichungen ein und vereinfache:

$II)1{,}2=8a+4b-1{,}8+2$

$III)0=12a+4b-0{,}9$

Lösen des Gleichungssystem

Nach Verrechnung aller Konstanten hat das System die Form:

$I) 1=8a+4b\\ II)0{,}9=12a+4b$

Löse dieses System zum Beispiel mit dem Additions/Subtraktionsverfahren:

$\def\arraystretch{1.25} \begin{array}{lrl} &1=&8a+4b\\ -&0{,}9=&12a+4b\\ \hline &0{,}1=&-4a&|:(-4)\\ &-\frac 1{40}=&a \end{array}$

Setze $a=-\frac 1 {40}$ in eine der Gleichungen ein, um b zu ermitteln:

$\displaystyle 1$	$=$	$\displaystyle 8\cdot(-\frac{1}{40})+4b$
$\displaystyle 1$	$=$	$\displaystyle -\frac{1}{5}+4b$	$\displaystyle +\frac{1}{5}$
$\displaystyle 1{,}2$	$=$	$\displaystyle 4b$	$\displaystyle :4$
$\displaystyle 0{,}3$	$=$	$\displaystyle b$

Der Funktionsterm lautet also $f(x)=-\frac 1 {40}x^3+0{,}3x^2-0{,}9x+2$

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Im Folgenden wird die Funktion $g$ mit $g(x)=f(x)=-0{,}025\left(x^{3}-12 x^{2}+36 x-80\right)$ und der Definitionsmenge $D_{g}=[0 ; 7]$ betrachtet. Der Graph von $g$ in einem kartesischen Koordinatensystem wird mit $\mathrm{G}_{\mathrm{g}}$ bezeichnet.

Bestimmen Sie jeweils die Art und die Koordinaten aller Extrempunkte von $\mathrm{G}_{\mathrm{g}}$ und geben Sie die Wertemenge $W_{g}$ von $g$ an. (9 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen

Lage der Randextrema

Da beide Ränder des Definitionsbereichs eingeschlossen sind, gibt es zwei Randextrempunkte, deren Lage du durch Einsetzen in g erhältst:

$g(0)=2$

$g(7)=1{,}825$

Die Art dieser Extremstellen erhältst du am einfachsten, wenn du, gemeinsam mit den normalen Extremstellen, eine Monotonietabelle anlegst.

Lage weitere Extremstellen

Bestimme die anderen Extremstellen mithilfe der 1. Ableitung:

$g'(x)=-0{,}025(3x^2-24x+36)$

Du brauchst die Nullstellen der 1. Ableitung:

$\displaystyle g'\left(x\right)$	$=$	$\displaystyle 0$
$\displaystyle -0{,}025\left(3x^2-24x+36\right)$	$=$	$\displaystyle 0$	$\displaystyle :\left(-0{,}025\right)$
$\displaystyle 3x^2-24x+36$	$=$	$\displaystyle 0$

Bestimme die Nullstellen mit der Mitternachtsformel:

$x_{1/2}=\frac{-(-24)\pm\sqrt{(-24)^2-4\cdot 3\cdot 36}}{2\cdot 3}$

$x_1=2$ und $x_2=6$

Beide Nullstellen liegen im Definitionsbereich und es handelt sich bei beiden Nullstellen von $g'$ um Extremstellen von $g$ , da es einfache Nullstellen von $g'$ sind)

Ermittele die y-Koordinate dieser Extremstellen:

$g(2)=1{,}2$

$g(6)=2$

Art der Extremstellen

Fertige eine Monotonietabelle an, um die Art aller Extremstellen zu bestimmen.

x	0	<x<	2	<x<	6	<x<	7
VZ $g'$		-	0	+	0	-
$G_g$	RHOP	$\searrow$	TIP	$\nearrow$	HOP	$\searrow$	RTIP

Es gibt also die Extremstellen

$RHOP(0|2), TIP(2|1{,}2), HOP(6|2), RTIP(7|1{,}825)$

Wertemenge

Der kleinste und größte y-Wert der Extrempunkte legt die Wertemenge fest:

$W=[1{,}2;2]$

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

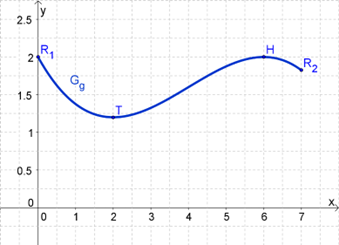
Zeichnen Sie den Graphen $\mathrm{G}_{\mathrm{g}}$ unter Verwendung aller bisherigen Ergebnisse und weiterer geeigneter Funktionswerte für $0 \leq x \leq 7$ in ein Koordinatensystem.
Maßstab für die $x$ -Achse: $1 \mathrm{LE}=1 \mathrm{~cm}$ , für die $y$ -Achse: $1 \mathrm{LE}=2 \mathrm{~cm}$
(4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
Beachte, dass auf der y-Achse bei 1 cm erst die 0,5 markiert wird.
Beim Eintragen der Funktionswerte musst du diese geänderte Skalierung ebenfalls beachten.
Zeichne nicht über die Definitionsmenge $D=[0;7]$ hinaus!
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die y-Achse hat einen veränderten Maßstab
Fertige eine Wertetabelle an und zeichne den Graphen. Halte dabei die Definitionsmenge ein!
Der Graph $\mathrm{G}_{\mathrm{g}}$ , die $\mathrm{x}$ -Achse und die beiden Geraden mit den Gleichungen $\mathrm{x}=2$ und $\mathrm{x}=6$ schließen ein endliches Flächenstück ein. Berechnen Sie die Maßzahl des Flächeninhalts dieses Flächenstücks. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bestimmtes Integral berechnen
Da das gesamte Flächenstück oberhalb der x-Achse liegt, kannst du den Flächeninhalt direkt mit dem bestimmten Integral berechnen:
$A=\int_2^6g(x)dx=[-0{,}025\cdot(\frac 1 4x^4-4x^3+18x^2-80x)]^6_2=9{,}3-2{,}9=6{,}4$
Die Fläche ist also $6{,}4 FE$ groß
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme den Wert des bestimmten Integrals