Teil 2 Analysis 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgaben zum Ausdrucken als PDF findest du hier.

Bei der Bearbeitung der Aufgaben dürfen Hilfsmittel verwendet werden

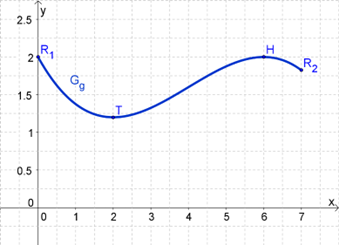
Der Graph der Funktion $f$ mit der Definitionsmenge $D_{f}=\R$ schneidet in einem kartesischen Koordinatensystem die $y$ -Achse beim Wert $y=2$ und verläuft durch den Extrempunkt $\mathrm{E}(2 \mid 1{,}2)$ . Außerdem ist bekannt, dass der Funktionsterm durch $f(x)=a x^{3}+b x^{2}-0{,}9 x+c$ mit $a, b, c \in I R$ und $a \neq 0$ dargestellt werden kann.

Bestimmen Sie im Funktionsterm von $\mathrm{f}$ die Werte der Parameter $\mathrm{a}, \mathrm{b}$ und $\mathrm{c}$ . (6 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steckbriefaufgaben

Aufstellen der Bedingungsgleichungen

Die Funktion $f(x)=ax^3+bx^2-0{,}9x+c$ hat die Ableitung:

$f'(x)=3ax^2+2bx-0{,}9$

Verwende das für die Bedingungsgleichungen:

"schneidet die y-Achse beim Wert $y=2$ " bedeutet, dass $f(0)=2$
"verläuft durch den Extrempunkt E(2|1,2)" bedeutet:
- $f(2)=1{,}2$
- $f'(2)=0$

Übersetzen in ein Gleichungssystem

Daraus erhältst du die drei Gleichungen

$I) 2=a\cdot 0^3+b\cdot 0^2-0{,}9\cdot 0+c\\ II) 1{,}2=a\cdot 2^3+b\cdot 2^2-0{,}9\cdot 2+c\\ III)0=3a\cdot 2^2+2b\cdot 2 - 0{,}9$

Aus Gleichung I) erhältst du direkt $I)2=c$

Setze c in die anderen beiden Gleichungen ein und vereinfache:

$II)1{,}2=8a+4b-1{,}8+2$

$III)0=12a+4b-0{,}9$

Lösen des Gleichungssystem

Nach Verrechnung aller Konstanten hat das System die Form:

$I) 1=8a+4b\\ II)0{,}9=12a+4b$

Löse dieses System zum Beispiel mit dem Additions/Subtraktionsverfahren:

$\def\arraystretch{1.25} \begin{array}{lrl} &1=&8a+4b\\ -&0{,}9=&12a+4b\\ \hline &0{,}1=&-4a&|:(-4)\\ &-\frac 1{40}=&a \end{array}$

Setze $a=-\frac 1 {40}$ in eine der Gleichungen ein, um b zu ermitteln:

$\displaystyle 1$	$=$	$\displaystyle 8\cdot(-\frac{1}{40})+4b$
$\displaystyle 1$	$=$	$\displaystyle -\frac{1}{5}+4b$	$\displaystyle +\frac{1}{5}$
$\displaystyle 1{,}2$	$=$	$\displaystyle 4b$	$\displaystyle :4$
$\displaystyle 0{,}3$	$=$	$\displaystyle b$

Der Funktionsterm lautet also $f(x)=-\frac 1 {40}x^3+0{,}3x^2-0{,}9x+2$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Im Folgenden wird die Funktion $g$ mit $g(x)=f(x)=-0{,}025\left(x^{3}-12 x^{2}+36 x-80\right)$ und der Definitionsmenge $D_{g}=[0 ; 7]$ betrachtet. Der Graph von $g$ in einem kartesischen Koordinatensystem wird mit $\mathrm{G}_{\mathrm{g}}$ bezeichnet.

Bestimmen Sie jeweils die Art und die Koordinaten aller Extrempunkte von $\mathrm{G}_{\mathrm{g}}$ und geben Sie die Wertemenge $W_{g}$ von $g$ an. (9 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen

Lage der Randextrema

Da beide Ränder des Definitionsbereichs eingeschlossen sind, gibt es zwei Randextrempunkte, deren Lage du durch Einsetzen in g erhältst:

$g(0)=2$

$g(7)=1{,}825$

Die Art dieser Extremstellen erhältst du am einfachsten, wenn du, gemeinsam mit den normalen Extremstellen, eine Monotonietabelle anlegst.

Lage weitere Extremstellen

Bestimme die anderen Extremstellen mithilfe der 1. Ableitung:

$g'(x)=-0{,}025(3x^2-24x+36)$

Du brauchst die Nullstellen der 1. Ableitung:

$\displaystyle g'\left(x\right)$	$=$	$\displaystyle 0$
$\displaystyle -0{,}025\left(3x^2-24x+36\right)$	$=$	$\displaystyle 0$	$\displaystyle :\left(-0{,}025\right)$
$\displaystyle 3x^2-24x+36$	$=$	$\displaystyle 0$

Bestimme die Nullstellen mit der Mitternachtsformel:

$x_{1/2}=\frac{-(-24)\pm\sqrt{(-24)^2-4\cdot 3\cdot 36}}{2\cdot 3}$

$x_1=2$ und $x_2=6$

Beide Nullstellen liegen im Definitionsbereich und es handelt sich bei beiden Nullstellen von $g'$ um Extremstellen von $g$ , da es einfache Nullstellen von $g'$ sind)

Ermittele die y-Koordinate dieser Extremstellen:

$g(2)=1{,}2$

$g(6)=2$

Art der Extremstellen

Fertige eine Monotonietabelle an, um die Art aller Extremstellen zu bestimmen.

x	0	<x<	2	<x<	6	<x<	7
VZ $g'$		-	0	+	0	-
$G_g$	RHOP	$\searrow$	TIP	$\nearrow$	HOP	$\searrow$	RTIP

Es gibt also die Extremstellen

$RHOP(0|2), TIP(2|1{,}2), HOP(6|2), RTIP(7|1{,}825)$

Wertemenge

Der kleinste und größte y-Wert der Extrempunkte legt die Wertemenge fest:

$W=[1{,}2;2]$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Zeichnen Sie den Graphen $\mathrm{G}_{\mathrm{g}}$ unter Verwendung aller bisherigen Ergebnisse und weiterer geeigneter Funktionswerte für $0 \leq x \leq 7$ in ein Koordinatensystem.
Maßstab für die $x$ -Achse: $1 \mathrm{LE}=1 \mathrm{~cm}$ , für die $y$ -Achse: $1 \mathrm{LE}=2 \mathrm{~cm}$
(4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
Beachte, dass auf der y-Achse bei 1 cm erst die 0,5 markiert wird.
Beim Eintragen der Funktionswerte musst du diese geänderte Skalierung ebenfalls beachten.
Zeichne nicht über die Definitionsmenge $D=[0;7]$ hinaus!
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die y-Achse hat einen veränderten Maßstab
Fertige eine Wertetabelle an und zeichne den Graphen. Halte dabei die Definitionsmenge ein!
Der Graph $\mathrm{G}_{\mathrm{g}}$ , die $\mathrm{x}$ -Achse und die beiden Geraden mit den Gleichungen $\mathrm{x}=2$ und $\mathrm{x}=6$ schließen ein endliches Flächenstück ein. Berechnen Sie die Maßzahl des Flächeninhalts dieses Flächenstücks. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bestimmtes Integral berechnen
Da das gesamte Flächenstück oberhalb der x-Achse liegt, kannst du den Flächeninhalt direkt mit dem bestimmten Integral berechnen:
$A=\int_2^6g(x)dx=[-0{,}025\cdot(\frac 1 4x^4-4x^3+18x^2-80x)]^6_2=9{,}3-2{,}9=6{,}4$
Die Fläche ist also $6{,}4 FE$ groß
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme den Wert des bestimmten Integrals

Beim Aufladen des Akkus eines Smartphones fließt ein Ladestrom von 2000 Milliampere. Sobald der Akku optimal geladen ist, verringert das Ladegerät den Ladestrom um eine Überladung zu vermeiden.

Die Funktion $I$ mit $I(t)=2000 \cdot 0{,}5^{\frac{t}{4{,}88}}$ und $t \in D_{1} \subset \mathbb{R}$ modelliert den Verlauf des Ladestroms ab dem Erreichen der optimalen Akkuladung zur Zeit $t=0$ bis zur endgültigen Abschaltung des Ladegeräts zur Zeit $t_{\text {end }}>0$ . Die Funktionswerte von I entsprechen der Stärke des Ladestroms in Milliampere und $t$ entspricht der Zeit in Minuten.

Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.

Zeigen Sie, dass sich der Funktionsterm näherungsweise auch in der Form $\tilde{I}(t)=2000 \cdot e^{-0{,}142 \cdot t}$ schreiben lässt. (3 BE)

Das Ladegerät schaltet sich komplett ab, wenn die Ladestromstärke auf 100 Milliampere abgesunken ist. Ermitteln Sie $t_{\text {end }}$ unter Verwendung des Funktionsterms aus 2.1. Runden Sie das Ergebnis auf ganze Minuten und geben Sie eine sinnvolle Definitionsmenge für $\tilde{\mathrm{I}}$ an. (4 BE)

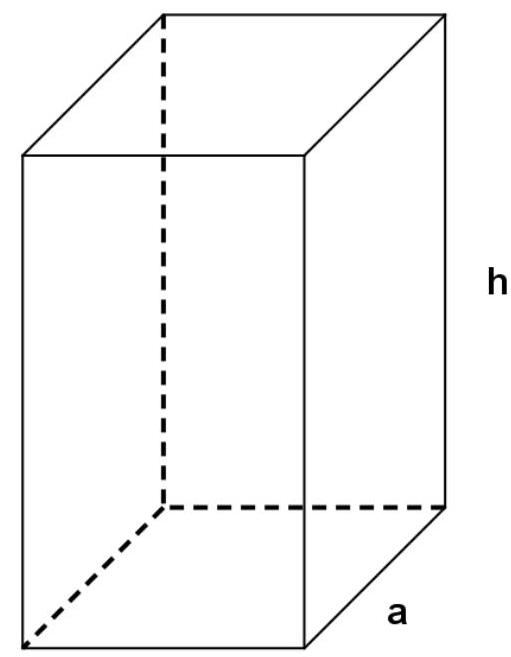
Die Firma FACTUS soll für einen Süßwarenhersteller quaderförmige Verpackungen für Schokoladenbonbons produzieren. Der Auftraggeber verlangt, dass die Verpackung eine quadratische Grundfläche aufweist und dass die Summe aus Länge, Breite und Höhe $45 \mathrm{~cm}$ beträgt, damit der Verpackungsautomat die gefalteten Verpackungen verarbeiten und befüllen kann. Die Seitenlänge der quadratischen Grundfläche wird mit a bezeichnet.

Die Werte der Funktion $V: a \mapsto V(a)$ geben jeweils das Volumen der Verpackung in $\mathrm{cm}^{3}$ an. Damit die Verpackung handlich bleibt, soll die Seitenlänge a der Grundfläche mindestens $10 \mathrm{~cm}$ und höchstens $20 \mathrm{~cm}$ betragen.

Bei den Berechnungen kann auf das Mitführen der Einheiten verzichtet werden.

Bestimmen Sie einen Funktionsterm der Funktion V .
[ Mögliches Ergebnis: $\mathrm{V}(\mathrm{a})=45 \mathrm{a}^{2}-2 \mathrm{a}^{3}$ ]
(3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Hauptbedingung
Die Zielfunktion/Hauptbedingung beschreibt das Volumen des Quaders. Der Quader hat eine quadratische Grundfläche, deshalb gilt für das Volumen:
$V(a,h)=a^2\cdot h$
Nebenbedingung
Dein Ziel ist es, h in der Hauptbedingung loszuwerden. Du weißt aus der Aufgabenstellung, dass die Summe aus Länge, Breite und Höhe exakt 45 cm ist:
$a+a+h=45$
Forme diese Nebenbedingung nach h um:
$\displaystyle 2a+h$ $=$ $\displaystyle 45$ $\displaystyle -2a$
$\displaystyle h$ $=$ $\displaystyle 45-2a$
Nebenbedingung in Hauptbedingung
Ersetze h in der Hauptbedingung:
$\displaystyle V\left(a\right)$ $=$ $\displaystyle a^2\cdot\left(45-2a\right)$
$=$ $\displaystyle 45a^2-2a^3$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es handelt sich um eine Extremwertaufgabe.
Hier sollst du den Funktionsterm der Hauptbedingung in Abhängigkeit von a herausfinden.
Stelle eine Hauptbedingung auf
Stelle eine Nebenbedingung auf
Forme die Nebenbedingung nach h um und setze in die Hauptbedingung ein

Ermitteln Sie die Maße einer Verpackung der Firma FACTUS, die den Vorgaben entspricht und dabei maximales Volumen besitzt. Geben Sie die spezielle Form dieser Verpackung an und berechnen Sie das Volumen. (7 BE)

Die Firma FACTUS bekommt den Auftrag, 6000 würfelförmige und bedruckte Verpackungen mit einer Kantenlänge von $15 \mathrm{~cm}$ herzustellen.
Aus Kostengründen überlegt die Firma, ob sie den Druckauftrag an die eigene Druckerei FACTUS-Print geben soll oder ob das Angebot der Konkurrenzfirma PappDruck günstiger ist. Bei den Verpackungen werden alle Außenflächen außer der Bodenfläche bedruckt.
(4 BE)
Druckkosten
Rabatt
FACTUS-Print
8 Cent pro 1000 cm²
kein Rabatt
PappDruck
9 Cent pro Verpackung
Bedruckung jedes 10. Würfels gratis
Entscheiden Sie rechnerisch, welche Firma aus wirtschaftlicher Sicht den Druckauftrag bekommen sollte. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnung mittels Formeln
FACTUS-Print
Hier musst du wissen, wie groß die Oberfläche des Würfels ist. Der Karton ist nach oben offen, eine Seitenfläche ist ein Quadrat mit Seitenlänge $a=15$ :
$O=5\cdot (15\cdot 15)=1125 \quad[cm^2]$
Insgesamt sind es 6000 Würfel, also werden $6000\cdot1125 cm^2=6750000cm^2$ bedruckt.
Es sind 0,08€ pro $1000cm^2$ zu bezahlen, also:
$(6750000cm^2:1000cm^2)\cdot 0{,}08€=540€$
PappDruck
Da jeder 10. Würfel gratis ist, zahlst du nur 90% der Würfel.
Das sind $6000\cdot 0{,}9=5400$ Stück.
Pro Würfel zahlst du 0,09€:
$5400\cdot 0{,}09 €=486€$
Entscheidung
Es sollte bei PappDruck gedruckt werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme den Oberflächeninhalt der Verpackung
Berechne daraus den Preis bei FACTUS-Print
Bestimme, wie viele Würfel bei PappDruck bezahlt werden müssen und bestimme ebenfalls den Preis
Vergleiche die Preise und gib eine Empfehlung ab

	Druckkosten	Rabatt
FACTUS-Print	8 Cent pro 1000 cm²	kein Rabatt
PappDruck	9 Cent pro Verpackung	Bedruckung jedes 10. Würfels gratis

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle I\left(t\right)$	$=$	$\displaystyle 2000\cdot0{,}5^{\frac{t}{4{,}88}}$
	↓	Ziehe das t aus dem Zähler des Bruchs
	$=$	$\displaystyle 2000\cdot0{,}5^{\frac{1}{4{,}88}\cdot t}$
	↓	Verwende $b^{x\cdot y}=(b^x)^y$
	$=$	$\displaystyle 2000\cdot\left(0{,}5^{\frac{1}{4{,}88}}\right)^t$
	↓	Berechne den Wert in der Klammer
	$≈$	$\displaystyle 2000\cdot\left(0{,}8676\right)^t$

$\displaystyle \tilde{I}\left(t\right)$	$=$	$\displaystyle 2000\cdot e^{-0{,}142t}$
	↓	Verwende erneut $b^{x\cdot y}=(b^x)^y$
	$=$	$\displaystyle 2000\cdot\left(e^{-0{,}142}\right)^t$
	$=$	$\displaystyle 2000\cdot\left(0{,}8676\right)^t$
	$=$	$\displaystyle I\left(t\right)$

$\displaystyle 100$	$=$	$\displaystyle \tilde{I}\left(t\right)$
$\displaystyle 100$	$=$	$\displaystyle 2000\cdot e^{-0{,}142t}$	$\displaystyle :2000$
$\displaystyle \frac{1}{20}$	$=$	$\displaystyle e^{-0{,}142t}$
	↓	Verwende den ln
$\displaystyle \ln\left(\frac{1}{20}\right)$	$=$	$\displaystyle -0{,}142t$	$\displaystyle :\left(-0{,}142\right)$
$\displaystyle t$	$≈$	$\displaystyle 21{,}10$

$\displaystyle 90-6a$	$=$	$\displaystyle 0$	$\displaystyle +6a$
$\displaystyle 90$	$=$	$\displaystyle 6a$	$\displaystyle :6$
$\displaystyle 15$	$=$	$\displaystyle a$

Teil 2 Analysis 2

Aufstellen der Bedingungsgleichungen

Übersetzen in ein Gleichungssystem

Lösen des Gleichungssystem

Hast du eine Frage oder Feedback?

Lage der Randextrema

Lage weitere Extremstellen

Art der Extremstellen

Wertemenge

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Zeitpunkt bestimmen

Definitionsmenge

Hast du eine Frage oder Feedback?

Hauptbedingung

Nebenbedingung

Nebenbedingung in Hauptbedingung

Hast du eine Frage oder Feedback?

Randextrema

übrige Extrema

Höhe des Quaders und Form

Hast du eine Frage oder Feedback?

FACTUS-Print

PappDruck

Entscheidung

Hast du eine Frage oder Feedback?

$\displaystyle 2a+h$	$=$	$\displaystyle 45$	$\displaystyle -2a$
$\displaystyle h$	$=$	$\displaystyle 45-2a$

$\displaystyle V\left(a\right)$	$=$	$\displaystyle a^2\cdot\left(45-2a\right)$
	$=$	$\displaystyle 45a^2-2a^3$

$\displaystyle 0$	$=$	$\displaystyle V'\left(a\right)$
$\displaystyle 0$	$=$	$\displaystyle 90a-6a^2$
	↓	Klammere $a$ aus
$\displaystyle 0$	$=$	$\displaystyle a\left(90-6a\right)$