Die Firma FACTUS soll für einen Süßwarenhersteller quaderförmige Verpackungen für Schokoladenbonbons produzieren. Der Auftraggeber verlangt, dass die Verpackung eine quadratische Grundfläche aufweist und dass die Summe aus Länge, Breite und Höhe beträgt, damit der Verpackungsautomat die gefalteten Verpackungen verarbeiten und befüllen kann. Die Seitenlänge der quadratischen Grundfläche wird mit a bezeichnet.
Die Werte der Funktion geben jeweils das Volumen der Verpackung in an. Damit die Verpackung handlich bleibt, soll die Seitenlänge a der Grundfläche mindestens und höchstens betragen.
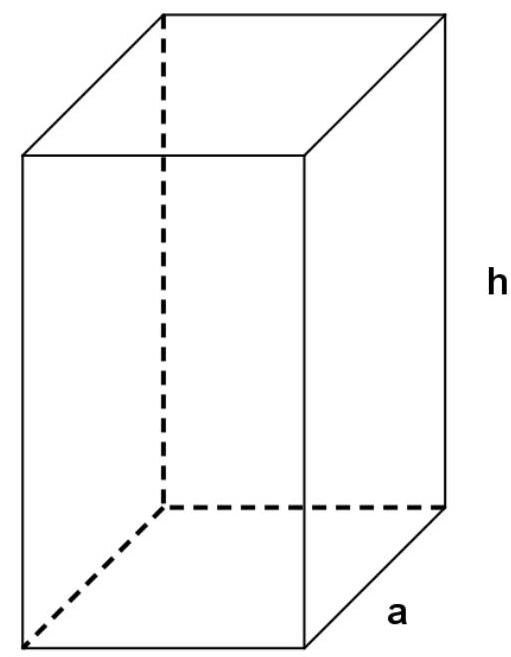
Bei den Berechnungen kann auf das Mitführen der Einheiten verzichtet werden.
Bestimmen Sie einen Funktionsterm der Funktion V .
[ Mögliches Ergebnis: ]
(3 BE)
Ermitteln Sie die Maße einer Verpackung der Firma FACTUS, die den Vorgaben entspricht und dabei maximales Volumen besitzt. Geben Sie die spezielle Form dieser Verpackung an und berechnen Sie das Volumen. (7 BE)
Die Firma FACTUS bekommt den Auftrag, würfelförmige und bedruckte Verpackungen mit einer Kantenlänge von herzustellen.
Aus Kostengründen überlegt die Firma, ob sie den Druckauftrag an die eigene Druckerei FACTUS-Print geben soll oder ob das Angebot der Konkurrenzfirma PappDruck günstiger ist. Bei den Verpackungen werden alle Außenflächen außer der Bodenfläche bedruckt.
(4 BE)
Druckkosten
Rabatt
FACTUS-Print
Cent pro
kein Rabatt
PappDruck
Cent pro Verpackung
Bedruckung jedes Würfels gratis
Entscheiden Sie rechnerisch, welche Firma aus wirtschaftlicher Sicht den Druckauftrag bekommen sollte. (4 BE)
