Aufgabe 3A
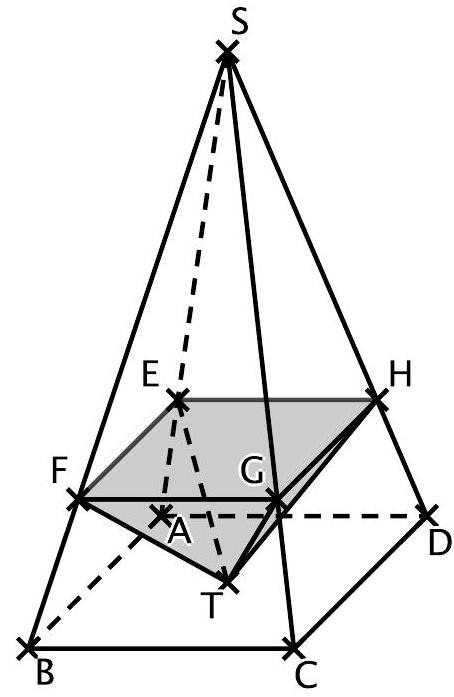
Die Abbildung zeigt die Pyramide mit
und .
Die Grundfläche ist quadratisch.
Der Schnittpunkt der Diagonalen der Grundfläche wird mit bezeichnet.
Geben Sie die Koordinaten des Punktes an.
Berechnen Sie den Inhalt der Oberfläche der Pyramide . (6BE)
Bestimmen Sie die Größe des Winkels zwischen den Kanten und . (3BE)
Der Mittelpunkt der Kante wird mit bezeichnet.
Untersuchen Sie, ob es einen Punkt auf der Kante gibt, für den das Dreieck im Punkt rechtwinklig ist. (5BE)
Die vier Punkte und liegen jeweils auf einer der vier vom Punkt ausgehenden Kanten und haben alle die -Koordinate (vgl. Abbildung).
Gegeben ist die folgende Lösung einer Aufgabe im Zusammenhang mit den betrachteten geometrischen Objekten:
liefert und damit und .
Geben Sie eine passende Aufgabenstellung an und erläutern Sie den Ansatz der gegebenen Lösung. (3BE)
Ermitteln Sie das Volumen der Pyramide . (3BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
