Aufgabe 3: Muster
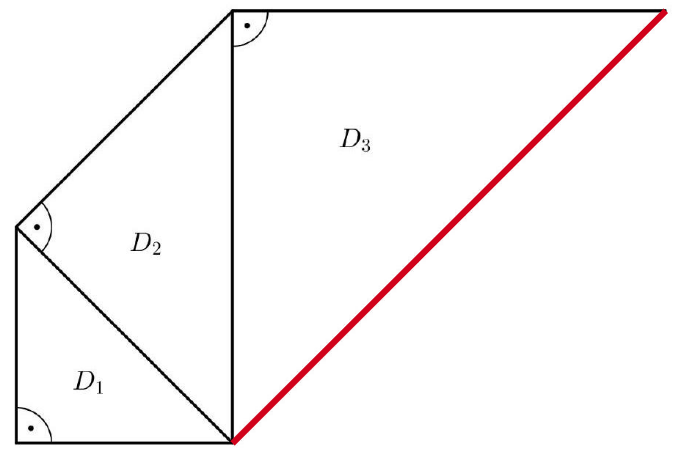
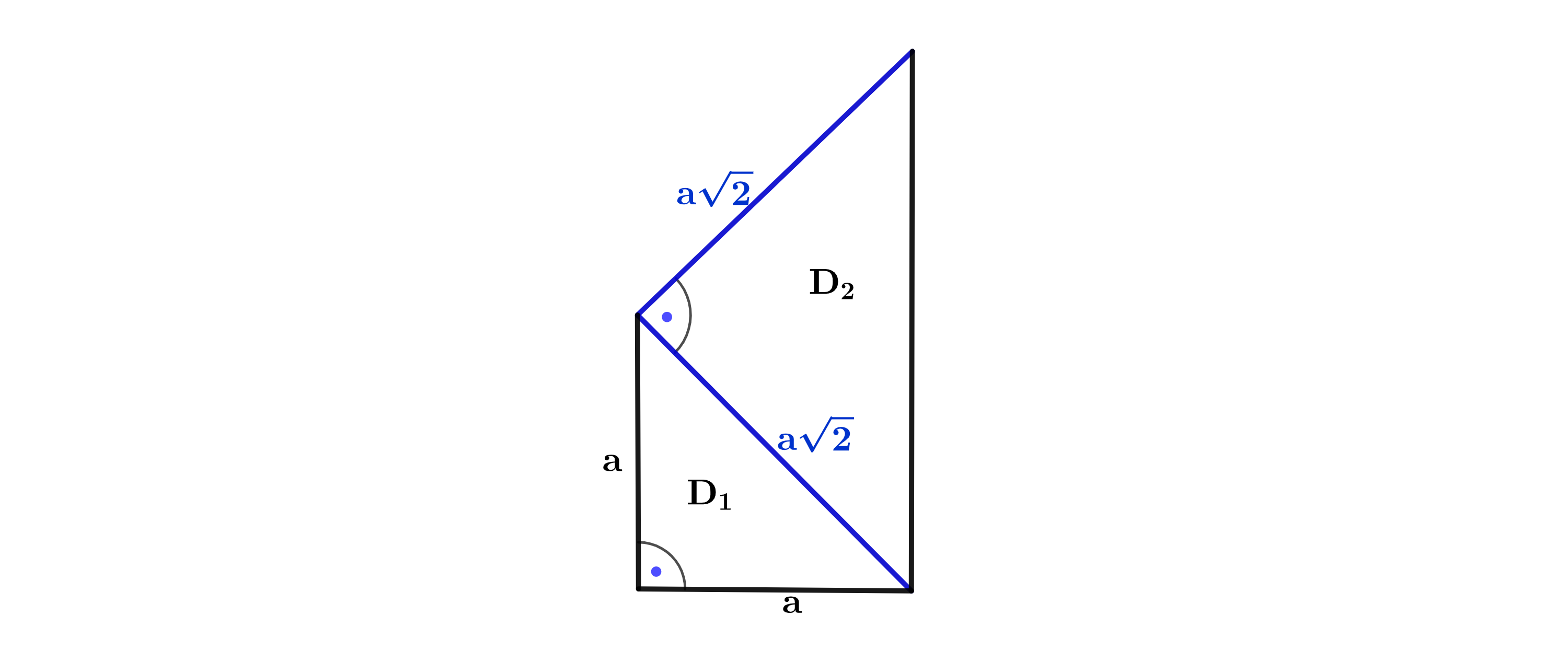
Jan möchte ein Muster aus rechtwinkligen gleichschenkligen Dreiecken konstruieren. Er beginnt mit dem Dreieck (Abbildung 1).
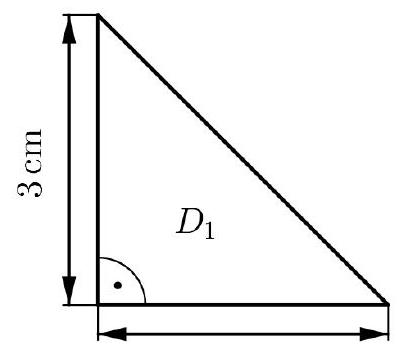
Abbildung 1: Dreieck
Zeige mit einer Rechnung, dass die Länge der Hypotenuse von Dreieck ca. beträgt. (3 P)
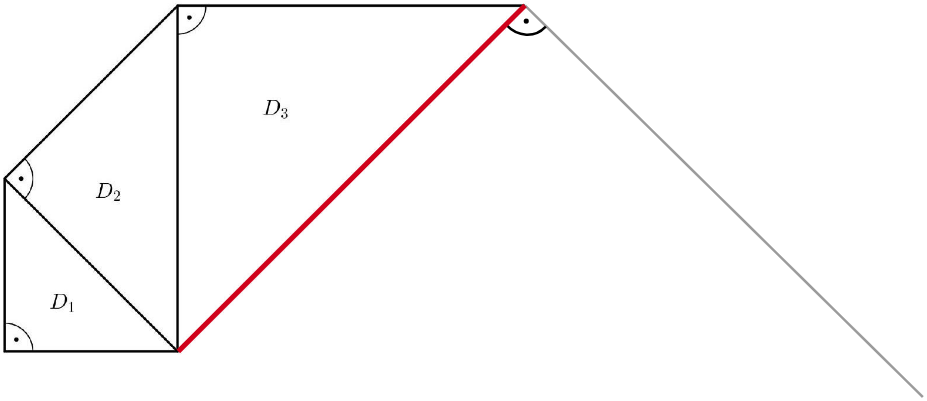
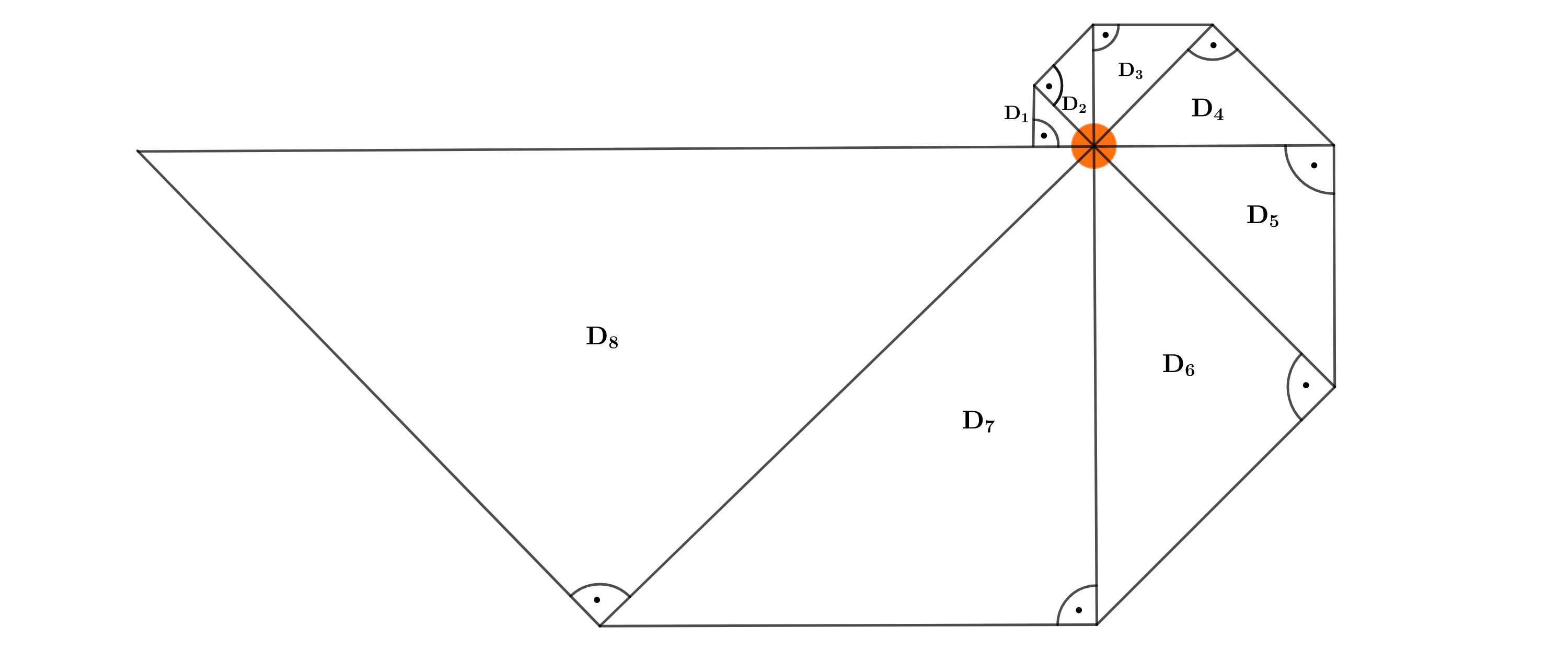
Jan setzt das Muster mit den beiden weiteren Dreiecken und fort (Abbildung 2).
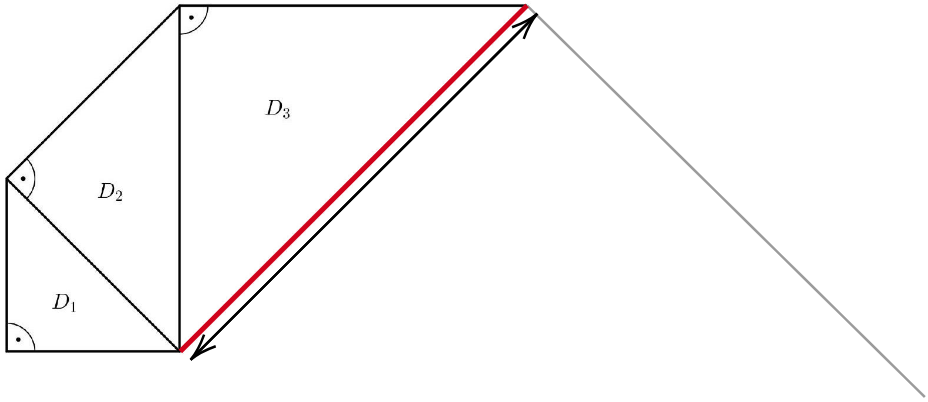
Ergänze das Dreieck zeichnerisch in Abbildung 2. Beschreibe, wie du vorgegangen bist. (4 P)
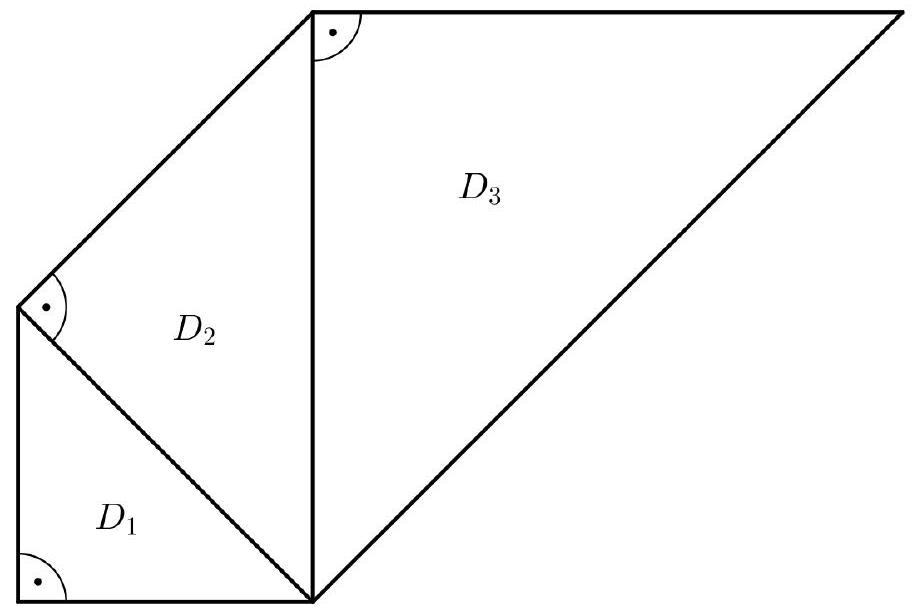
Abbildung 2: Muster bis Dreieck zu Teilaufgabe b) - d)
Jan kann nur acht Dreiecke zeichnen, ohne dass die Dreiecke sich überschneiden. Begründe dies mithilfe der Winkel. (2 P)
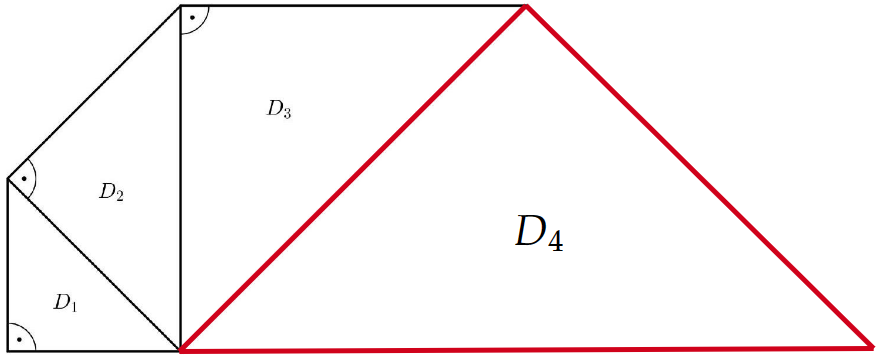
Zeige rechnerisch, dass der Flächeninhalt von Dreieck doppelt so groß ist wie der Flächeninhalt von Dreieck . (3 P)
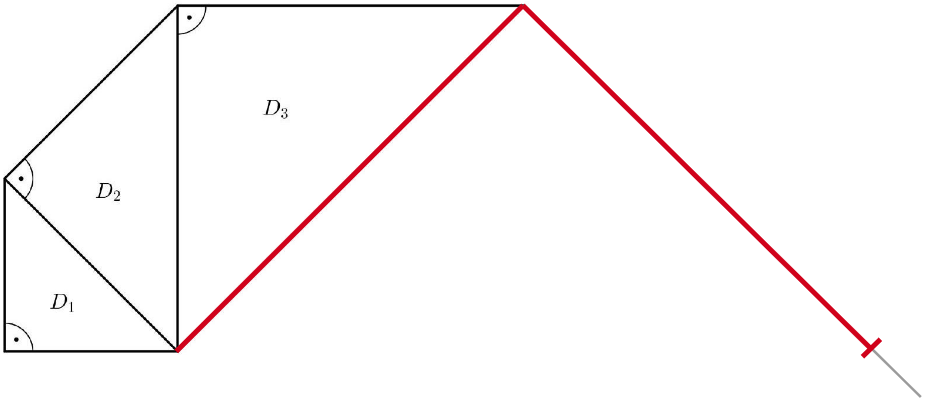
Jan berechnet weitere Flächeninhalte der Dreiecke in seinem Muster (Abbildung 3) und hält die Ergebnisse in einer Tabelle fest.

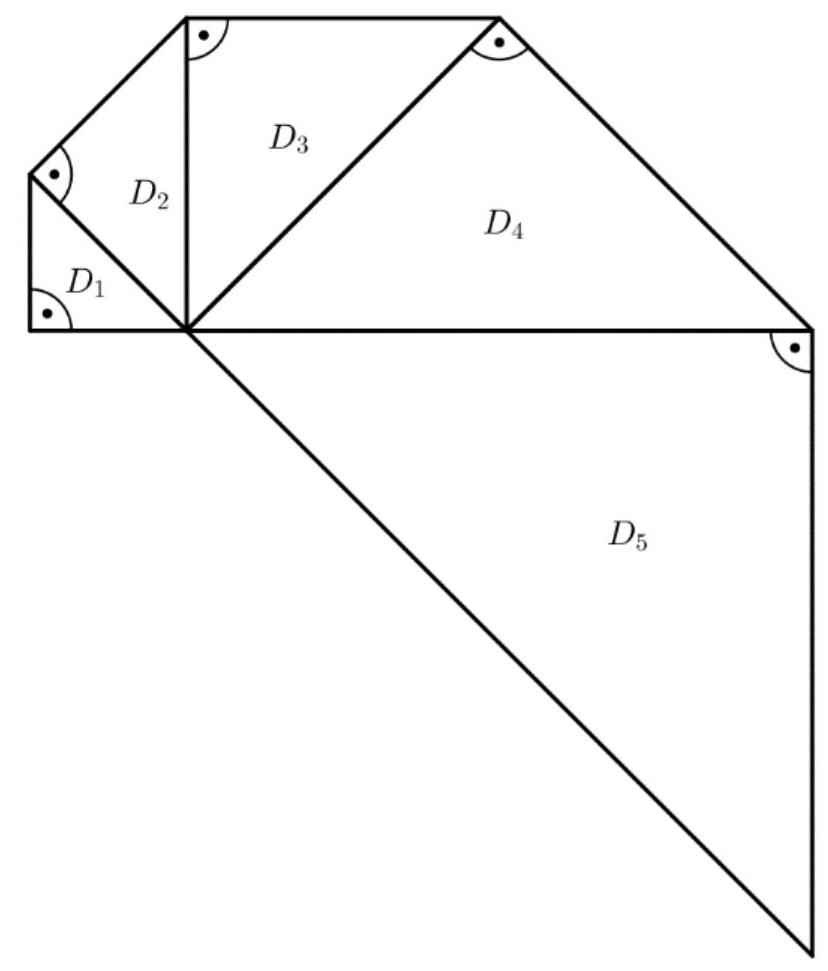
Abbildung 3: Muster bis Dreieck verkleinert dargestellt
Begründe, dass kein Dreieck in dem Muster einen Flächeninhalt von genau hat. (2 P)
Jan möchte das Muster aus Papier herstellen. Dazu schneidet er die einzelnen Dreiecke aus DIN-A4-Blättern ( 29,7 cm) aus. Jan behauptet: „Auch das Dreieck kann ich aus einem einzigen DIN-A4-Blatt ausschneiden.“
Entscheide begründet, ob Jans Behauptung zutrifft. (3 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?