Prüfungsteil 2 2021
🎓 Prüfungsbereich für Nordrhein-Westfalen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben aus dem Prüfungsteil 1 der ZP 10 Mathe 2021 für den MSA mit ausführlichen Musterlösungen. Diese Aufgaben wurden in einer anderen Variante zum Haupttermin 1 verwendet.
Für diese Aufgaben stehen dir in der Zentralen Prüfung 90 Minuten Bearbeitungszeit zur Verfügung. Taschenrechner und Formelsammlung sind für diesen Prüfungsteil erlaubt.
- 1
Aufgabe 1: Glaskugeln
Ein Unternehmen stellt lackierte Glaskugeln her (Abbildung 1).
Die Glaskugeln haben einen Durchmesser von .

Abbildung 1: Glaskugel
Berechne das Volumen einer Glaskugel. (3 P)
Nach der Herstellung der Form wird die Kugeloberfläche lackiert.
Mit einem Liter Farbe kann eine Fläche von lackiert werden.
Berechne, wie viele Glaskugeln mit einem Liter Farbe lackiert werden können. (4 P)
GlaskugelnEin Praktikant behauptet: „Für eine Glaskugel mit doppeltem Durchmesser benötigt man auch doppelt so viel Farbe.“
Hat der Praktikant recht? Begründe. (4 P)
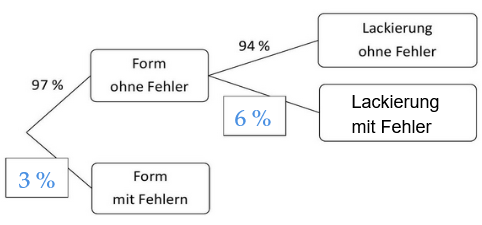
Bevor die lackierten Glaskugeln verpackt werden, durchlaufen sie eine Qualitätskontrolle. Zuerst wird die Form, danach die Lackierung auf Fehler kontrolliert. Alle Glaskugeln mit einem Fehler werden direkt aussortiert. Das Baumdiagramm zeigt die Anteile. Die Anteile werden im Folgenden als Wahrscheinlichkeiten gedeutet.
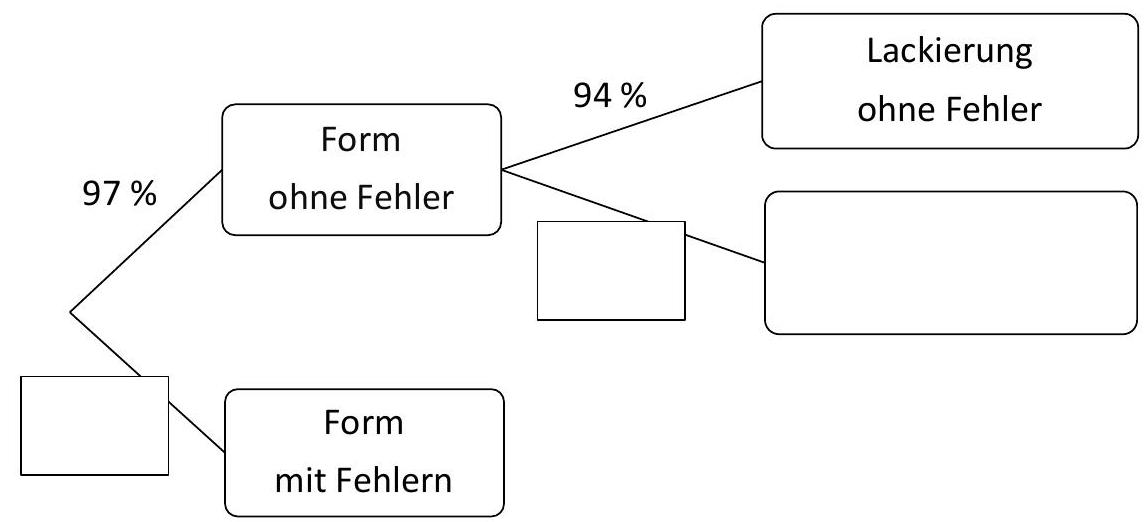
Ergänze die drei fehlenden Angaben im Baumdiagramm. (2 P)
Begründe, warum der untere Ast des Baumdiagramms nicht fortgeführt ist. (2 P)
Insgesamt werden 2000 Glaskugeln kontrolliert.
Berechne, wie viele fehlerfreie Glaskugeln zu erwarten sind. (3 P)
- 2
Aufgabe 2: Blobbing
Blobbing ist eine Wassersportart im Freien (Abbildung 1).
Eine vereinfachte Darstellung des Ablaufs ist in Abbildung 2 dargestellt. Beim Blobbing liegt ein mit Luft gefülltes Kissen im Wasser.
(1) Der Jumper springt vom Turm auf das Luftkissen.
(2) Auf der anderen Seite des Kissens ist der Blobber. Durch den Sprung befördert der Jumper den Blobber in die Luft.
(3) Der Blobber wird in die Luft geschleudert und landet dann im Wasser.

Abbildung 1: Ablauf eines Blobbingsprunges als überlagerte Aufnahme
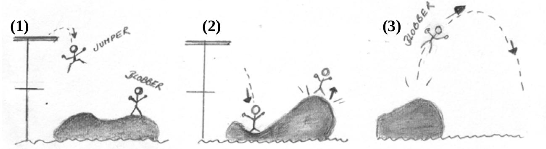
Abbildung 2: Vereinfachte Darstellung des Blobbing-Ablaufs (nicht maßstabsgetreu)
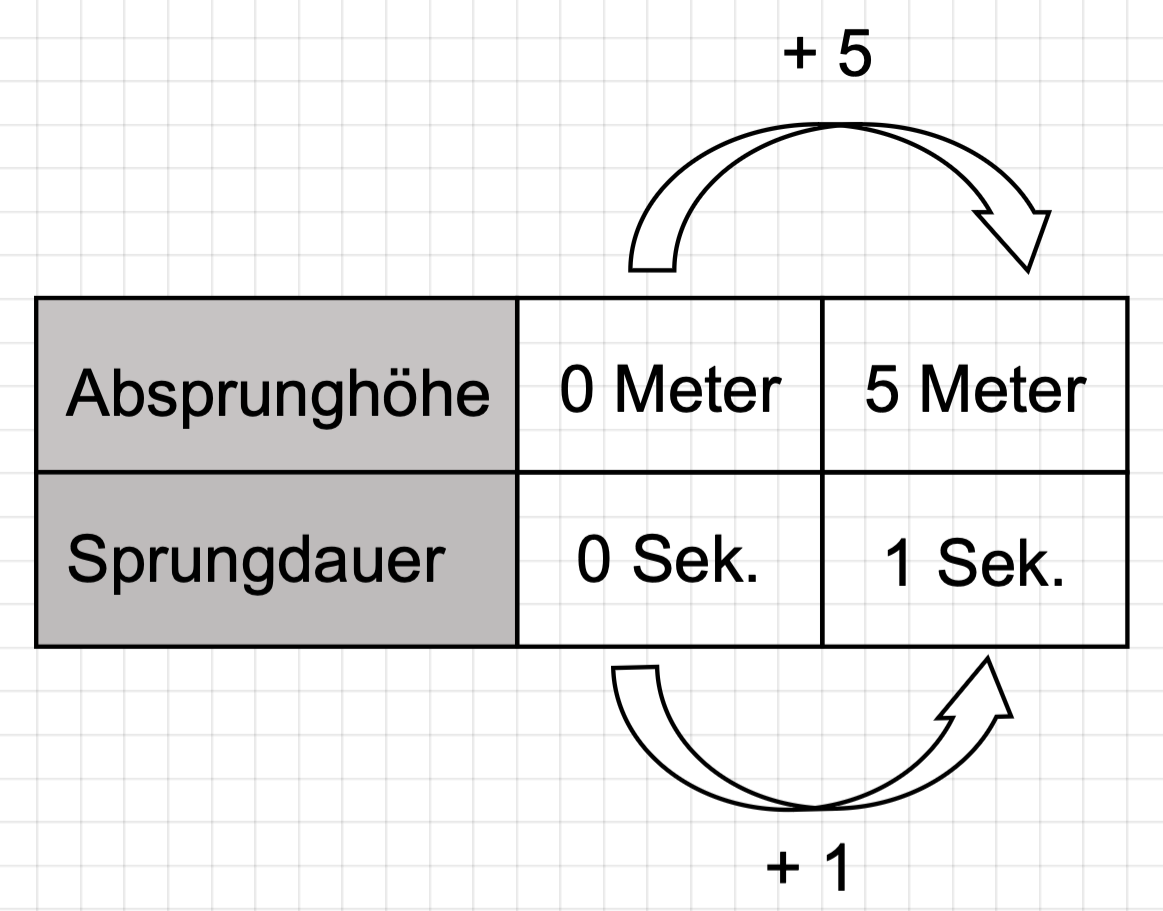
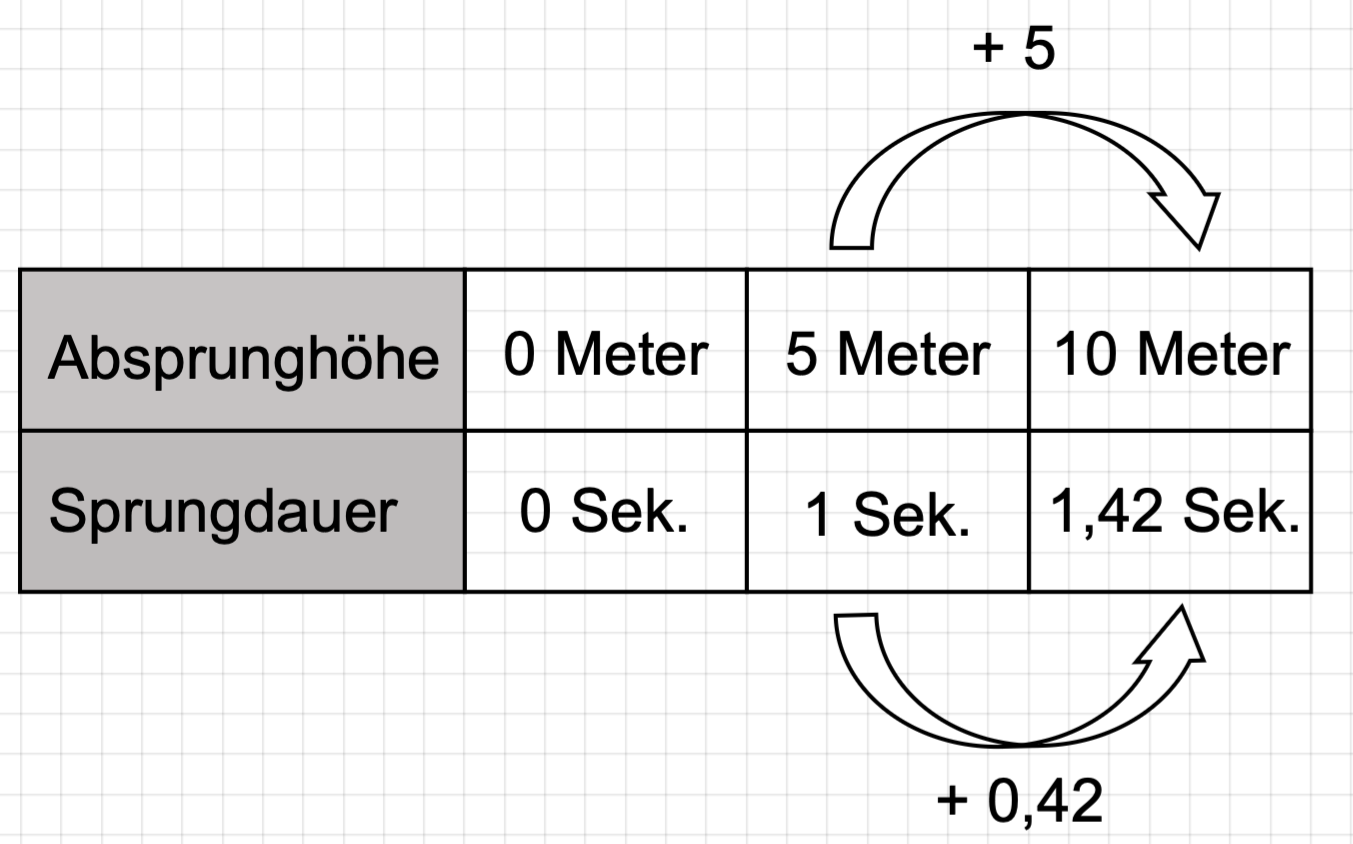
Der Jumper kann zwischen verschiedenen Absprunghöhen wählen. Ein Sprung aus fünf Meter Höhe dauert ca. 1 Sekunde. Ein Sprung aus zehn Meter Höhe dauert ca. 1,42 Sekunden.
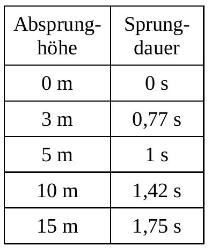
Tabelle 1: Sprungdauer in Abhängigkeit von der Absprunghöhe
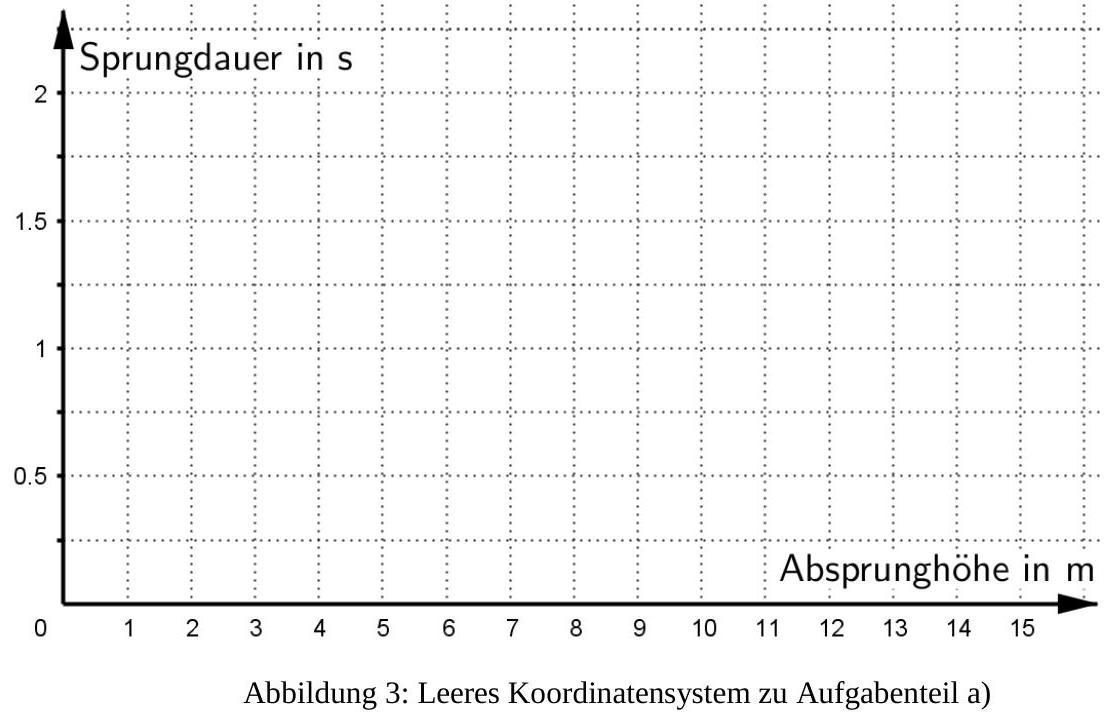
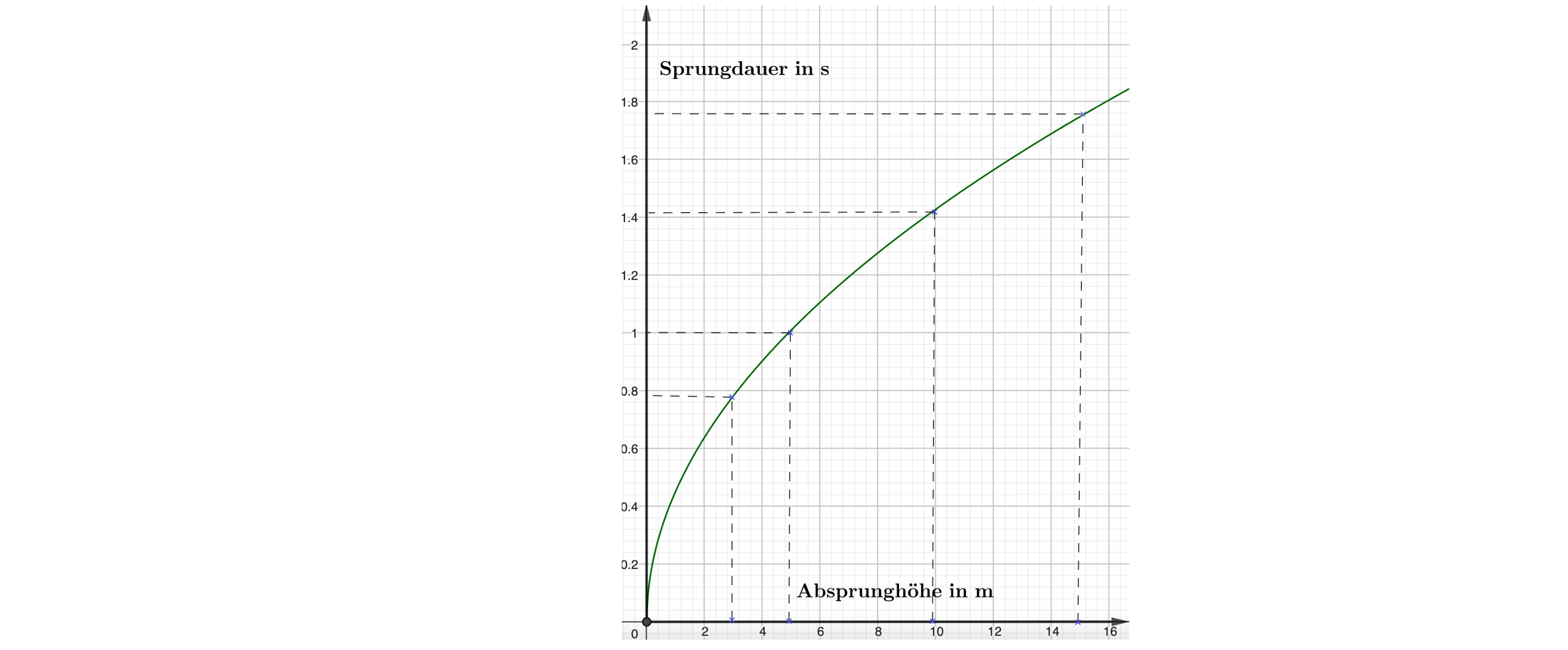
Skizziere zu den Werten aus Tabelle 1 den passenden Graphen in dem abgebildeten Koordinatensystem (Abbildung 3). (3 P)
Überprüfe, ob es zwischen der Absprunghöhe und der Sprungdauer einen linearen Zusammenhang gibt. Notiere deinen Lösungsweg. (2 P)
Abbildung 4 zeigt die Flugbahn eines Blobbers A.
Begründe mithilfe der Abbildung 4, dass sich die Funktion mit
zur Modellierung der Flugbahn von Blobber A eignet. (3 P)
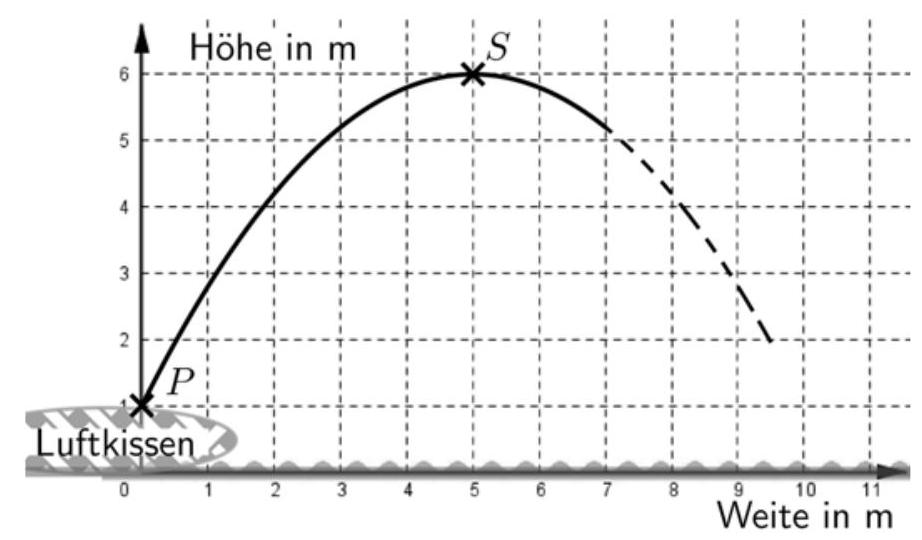
Abbildung 4: Flugbahn des Blobbers A
Zeige durch eine Rechnung, dass der Streckfaktor a hier beträgt. (2 P)
Die Flugbahn von Blobber A kann somit durch die Funktion mit beschrieben werden.
Die Funktionsgleichung mit beschreibt dieselbe Flugbahn.
Zeige durch Termumformungen, dass die Funktionsgleichungen von und dieselbe Parabel beschreiben. (3 P)
Berechne, wie weit Blobber A geflogen ist. (4 P)
Die Flugbahn eines zweiten Blobbers B wird mit der Funktion mit beschrieben.
Nenne eine Gemeinsamkeit und einen Unterschied der Flugbahn des zweiten Blobbers B im Vergleich zur Flugbahn von Blobber A. (2 P)
- 3
Aufgabe 3: Muster
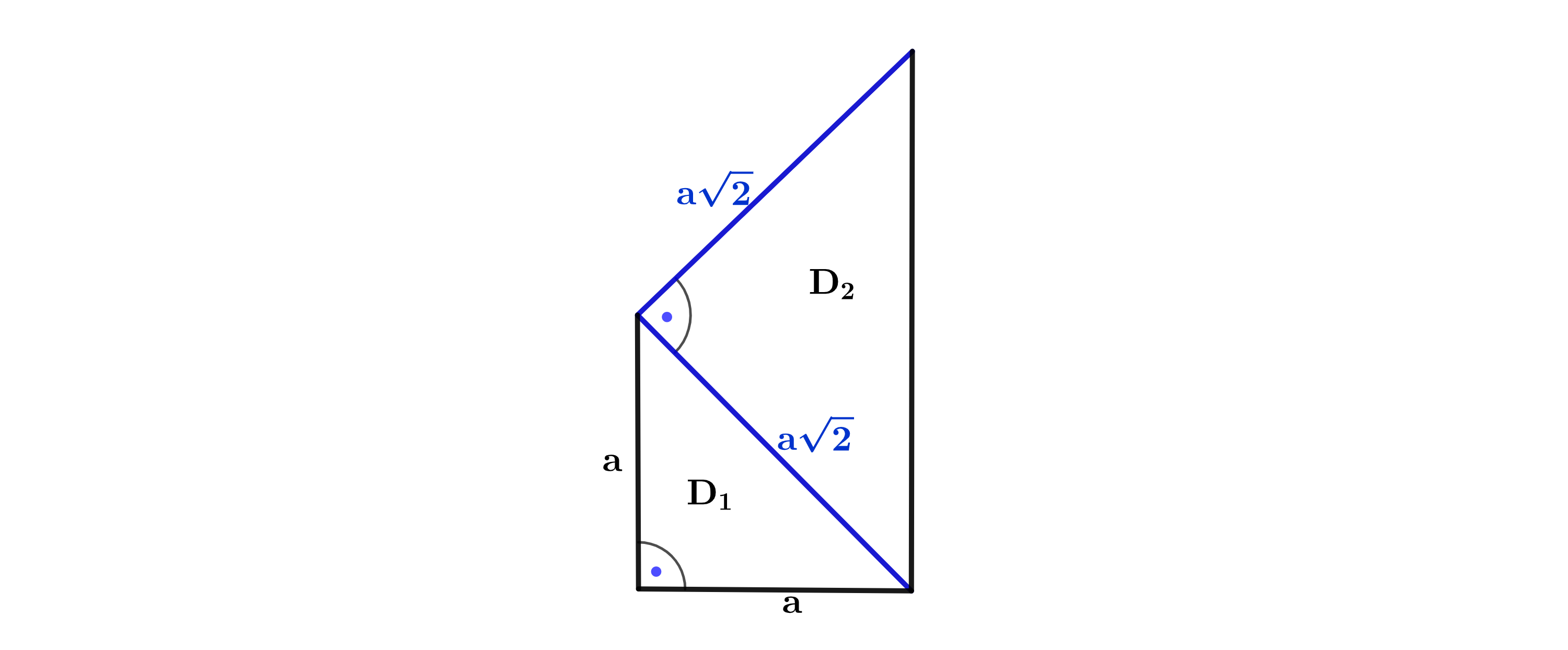
Jan möchte ein Muster aus rechtwinkligen gleichschenkligen Dreiecken konstruieren. Er beginnt mit dem Dreieck (Abbildung 1).
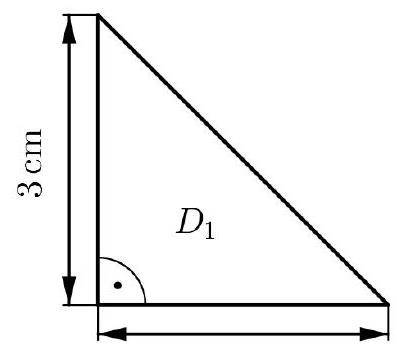
Abbildung 1: Dreieck
Zeige mit einer Rechnung, dass die Länge der Hypotenuse von Dreieck ca. beträgt. (3 P)
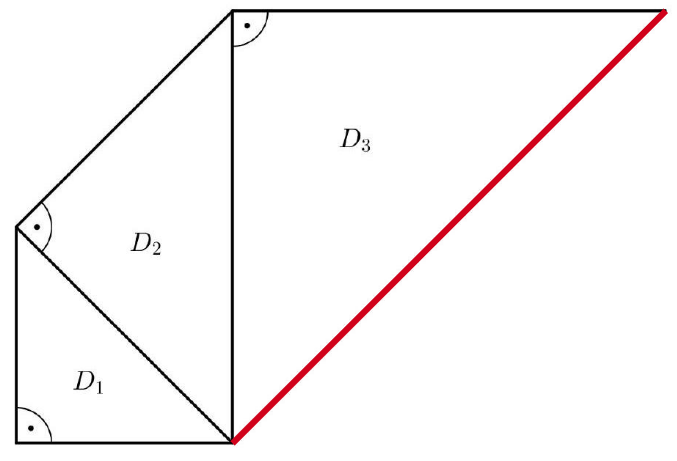
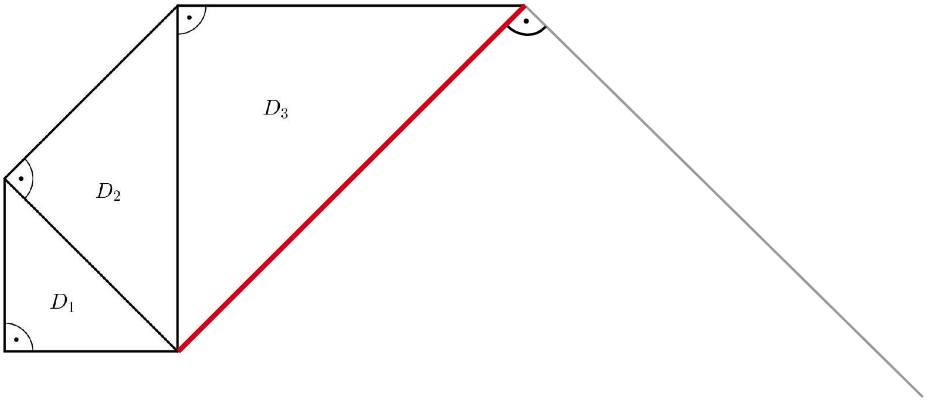
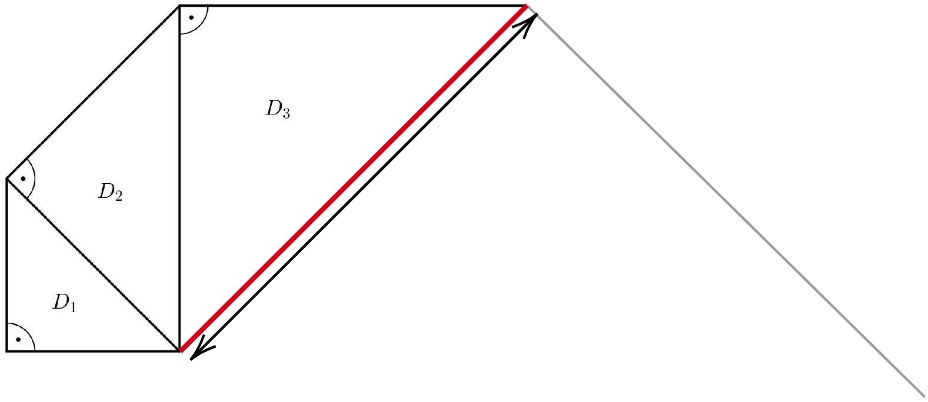
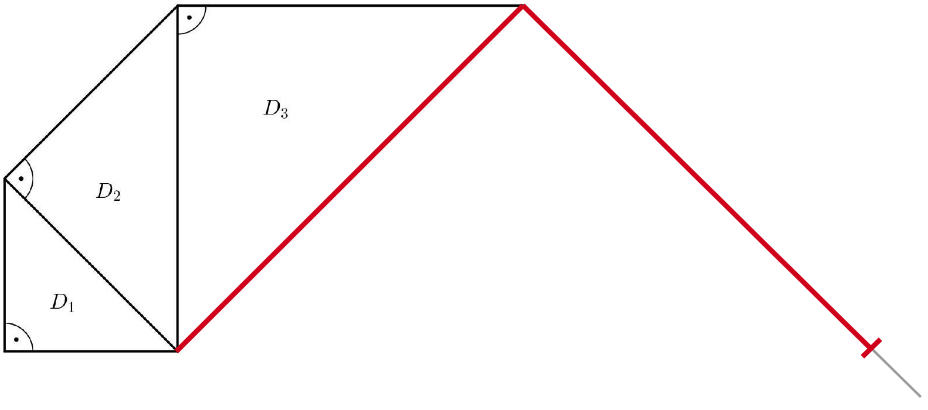
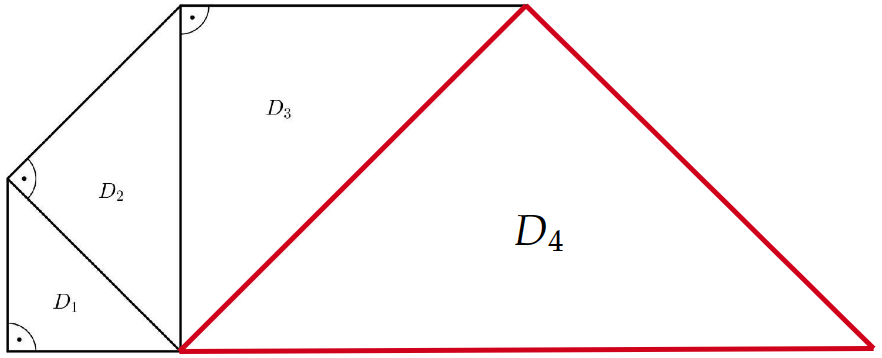
Jan setzt das Muster mit den beiden weiteren Dreiecken und fort (Abbildung 2).
Ergänze das Dreieck zeichnerisch in Abbildung 2. Beschreibe, wie du vorgegangen bist. (4 P)
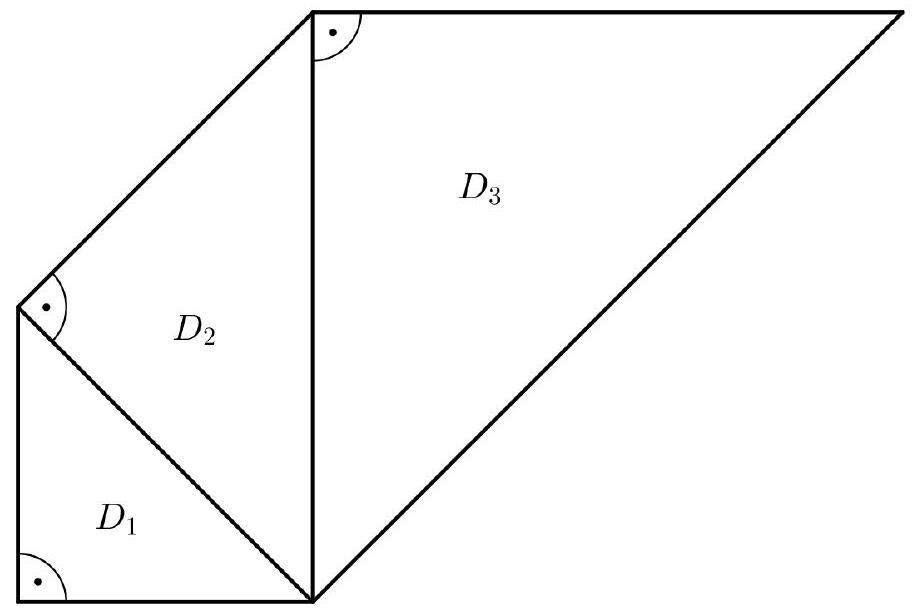
Abbildung 2: Muster bis Dreieck zu Teilaufgabe b) - d)
Jan kann nur acht Dreiecke zeichnen, ohne dass die Dreiecke sich überschneiden. Begründe dies mithilfe der Winkel. (2 P)
Zeige rechnerisch, dass der Flächeninhalt von Dreieck doppelt so groß ist wie der Flächeninhalt von Dreieck . (3 P)
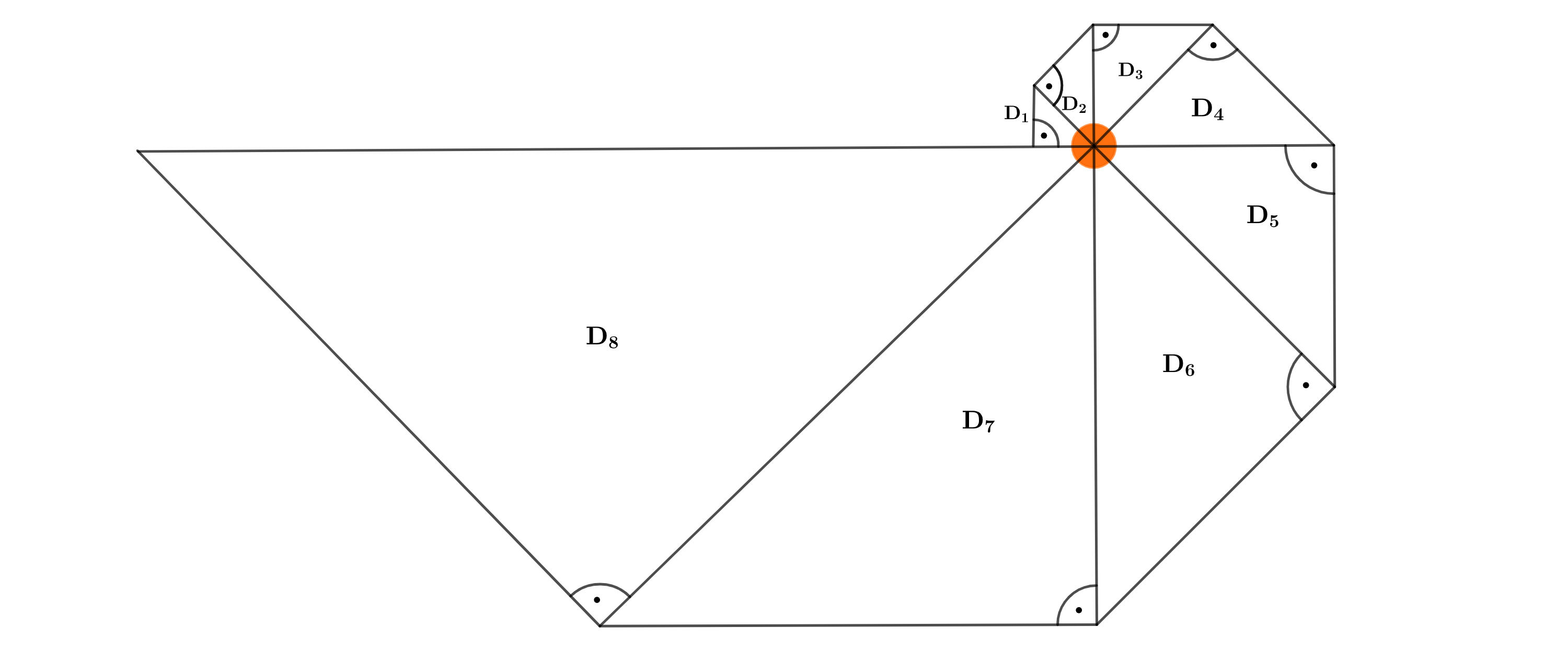
Jan berechnet weitere Flächeninhalte der Dreiecke in seinem Muster (Abbildung 3) und hält die Ergebnisse in einer Tabelle fest.

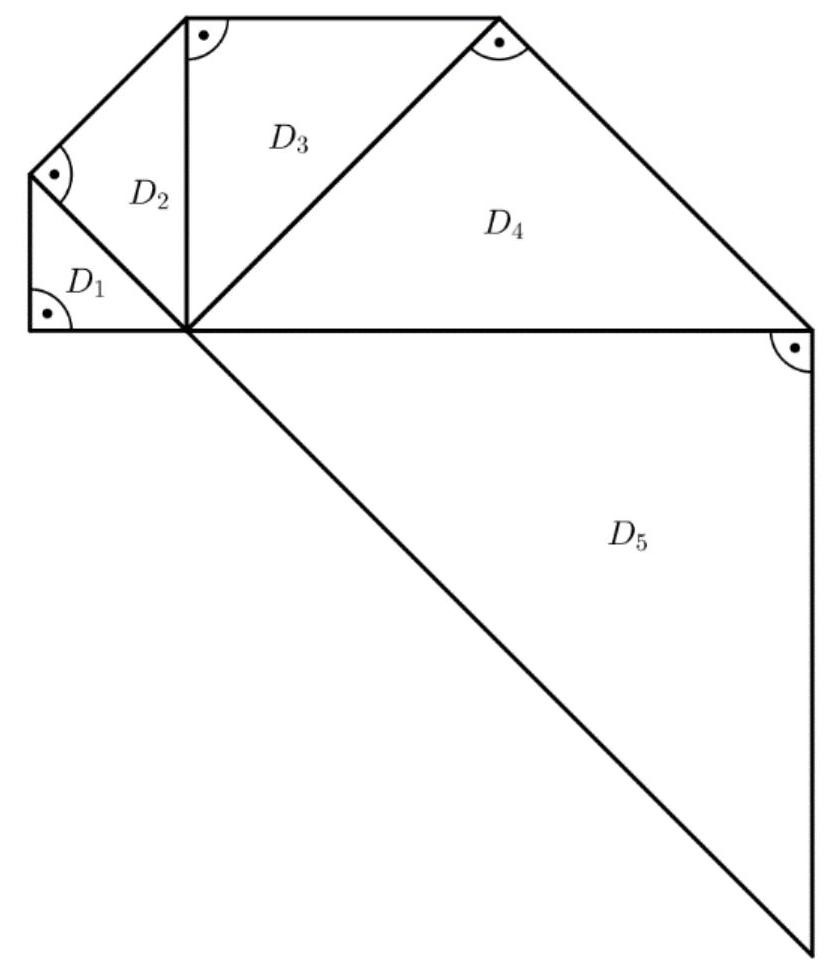
Abbildung 3: Muster bis Dreieck verkleinert dargestellt
Begründe, dass kein Dreieck in dem Muster einen Flächeninhalt von genau hat. (2 P)
Jan möchte das Muster aus Papier herstellen. Dazu schneidet er die einzelnen Dreiecke aus DIN-A4-Blättern ( 29,7 cm) aus. Jan behauptet: „Auch das Dreieck kann ich aus einem einzigen DIN-A4-Blatt ausschneiden.“
Entscheide begründet, ob Jans Behauptung zutrifft. (3 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?