Wahlteil - CAS - lernen mit Serlo!

Aufgabe 3C

Gegeben sind der Punkt $A (2 ∣ 2 ∣ 1)$ und die Gerade $g$ mit $\def\arraystretch{1.25} \vec{x}=\left(\begin{array}{c}0 \\ -2 \\ -1\end{array}\right)+s \cdot\left(\begin{array}{l}1 \\ 2 \\ 1\end{array}\right), s \in \mathbb{R}$ .

Zeigen Sie, dass $A$ ein Punkt von $g$ ist.
Die Ebene $E$ enthält den Punkt $A$ . $E$ und $g$ sind orthogonal zueinander.
Bestimmen Sie eine Gleichung für $E$ . (6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden und Ebenen im Raum
$A$ ist ein Punkt von $g$
Setze $A$ in $g$ ein:
$\begin{pmatrix}2 \\ 2 \\ 1\end{pmatrix}=\begin{pmatrix}0 \\ -2 \\ -1\end{pmatrix}+s\cdot\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$
Aus Gleichung $\mathrm{(I)}$ folgt, dass $s = 2$ ist. Die zweite und dritte Gleichung sind für $s = 2$ auch erfüllt. $A$ ist ein Punkt von $g$ .
Gleichung für $E$
$E$ und $g$ sind orthogonal zueinander, d.h. der Richtungsvektor der Geraden $\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$ ist der Normalenvektor der Ebene $E$ :
$E:\;\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}\circ \vec x=d$
Wegen $A\in E$ folgt: $\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}\circ \begin{pmatrix}2 \\ 2 \\ 1\end{pmatrix}=d\;\Rightarrow\;1\cdot 2+2\cdot 2+1\cdot 1=d\;\Rightarrow\;d=7$
$E:\; x+2y+z=7$ ist die gesuchte Ebenengleichung.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Setze $A$ in $g$ ein und prüfe, ob die $3$ Gleichungen für ein $s$ erfüllt sind.
$E$ und $g$ sind orthogonal zueinander, d.h. der Richtungsvektor der Geraden $\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$ ist der Normalenvektor der Ebene $E$ . Beachte auch, dass $A\in E$ ist.
Gegeben sind die Geraden $h_{a}$ mit $\def\arraystretch{1.25} \vec{x}=\left(\begin{array}{l}3 \\ 4 \\ 4\end{array}\right)+r \cdot\left(\begin{array}{c}a \\ -1 \\ 0\end{array}\right), r \in \mathbb{R}, a \in \mathbb{R}$ .
Geben Sie eine Gleichung der Ebene $H$ an, in der alle Geraden $h_{a}$ liegen.
Zeigen Sie, dass nicht jeder Punkt der Ebene $H$ auch ein Punkt von $h_{a}$ ist. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden und Ebenen im Raum
Gleichung der Ebene $H$ an, in der alle Geraden $h_{a}$ liegen
Es ist $\def\arraystretch{1.25} h_a:\;\vec{x}=\left(\begin{array}{l}3 \\ 4 \\ 4\end{array}\right)+r \cdot\left(\begin{array}{c}a \\ -1 \\ 0\end{array}\right)$
Die dritte Gleichung ist $z = 4$ . Das ist auch die Gleichung der Ebene $H$ .
Überprüfung: $h_a\cap H\;\Rightarrow\;0\cdot(3+r\cdot a)+0\cdot(4-r)+4+r\cdot 0=4\;\checkmark$
Nicht jeder Punkt der Ebene $H$ ist auch ein Punkt von $h_{a}$
Wähle z.B. den Punkt $B (0 ∣ 4 ∣ 4)$ . Es gilt: $B\in E$ . Prüfe, ob $B\in h_a$ :
$\displaystyle \begin{pmatrix}0 \\ 4 \\ 4\end{pmatrix}=\begin{pmatrix}3 \\ 4 \\ 4\end{pmatrix}+r\cdot\begin{pmatrix}a \\ -1 \\ 0\end{pmatrix}$
Aus Gleichung $\mathrm{(II)}$ folgt, dass $r = 0$ ist.
Dann ergibt sich Gleichung $\mathrm{(I)}$ : $0=3+0\cdot a\;\Rightarrow\;0=3$
Das ist aber ein Widerspruch, sodass $B\notin h_a$ .
Damit ist gezeigt, dass nicht jeder Punkt der Ebene $H$ auch ein Punkt von $h_{a}$ ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Betrachte die dritte Gleichung der Geradengleichung.
Teil 2
Wähle einen Punkt mit den Koordinaten $(x ∣ 4 ∣ 4)$ ( $x$ beliebig) und prüfe, ob dieser Punkt in der Ebene $H$ liegt.

Klassifizieren Sie die Geraden $h_{a}$ nach der Anzahl ihrer gemeinsamen Punkte mit der Ebene, mit der Gleichung $x + 2 y + z = 7$ . (4 BE)

Eine der Geraden von $h_{a}$ hat einen Schnittpunkt mit $g$ .

Berechnen Sie den Schnittpunkt und den Schnittwinkel. (8 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung zwischen zwei Geraden

Schnittpunkt von $h_{a}$ mit g

$h_a\cap g:$

$\displaystyle \begin{pmatrix}3 \\ 4 \\ 4\end{pmatrix}+r\cdot\begin{pmatrix}a \\ -1 \\ 0\end{pmatrix}$	$=$	$\displaystyle \begin{pmatrix}0 \\ -2 \\ -1\end{pmatrix}+s\cdot\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$	$\displaystyle -\begin{pmatrix}0 \\ -2 \\ -1\end{pmatrix}$
	↓	Bringe die Richtungsvektoren auf eine Seite der Gleichung und die Stützvektoren auf die andere Gleichungsseite.
$\displaystyle \begin{pmatrix}3 \\ 4 \\ 4\end{pmatrix}+r\cdot\begin{pmatrix}a \\ -1 \\ 0\end{pmatrix}-\begin{pmatrix}0 \\ -2 \\ -1\end{pmatrix}$	$=$	$\displaystyle s\cdot\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$	$\displaystyle -r\cdot\begin{pmatrix}a \\ -1 \\ 0\end{pmatrix}$
$\displaystyle \begin{pmatrix}3 \\ 4 \\ 4\end{pmatrix}-\begin{pmatrix}0 \\ -2 \\ -1\end{pmatrix}$	$=$	$\displaystyle s\cdot\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}-r\cdot\begin{pmatrix}a \\ -1 \\ 0\end{pmatrix}$
	↓	Berechne die Differenz.
$\displaystyle \begin{pmatrix}3 \\ 6 \\ 5\end{pmatrix}$	$=$	$\displaystyle s\cdot\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}-r\cdot\begin{pmatrix}a \\ -1 \\ 0\end{pmatrix}$

Aus der dritten Gleichung folgt $s = 5$ .

In Gleichung $\mathrm{(II)}$ wird $s = 5$ eingesetzt: $6=5\cdot 2+r\;\Rightarrow\;r=-4$ .

$r = - 4$ und $s = 5$ in Gleichung $\mathrm{(I)}$ eingesetzt ergibt: $3=5-(-4)\cdot a\;\Rightarrow\;-2=4\cdot a\;\Rightarrow\;a=-0{,}5$

Setzt man $s = 5$ in $g$ ein, erhält man den Schnittpunkt der beiden Geraden:

\displaystyle \vec x_S=\begin{pmatrix}0 \\ -2 \\ -1\end{pmatrix}+5\cdot\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}=\begin{pmatrix}5 \\ 8 \\ 4\end{pmatrix}\;\Rightarrow\;S(5|8|4)

Der Schnittpunkt von $h_{-0{,}5}$ mit $g$ hat die Koordinaten $S (5 ∣ 8 ∣ 4)$ .

Berechnen Sie den Schnittwinkel von $h_{-0{,}5}$ mit g

Der Richtungsvektor von $h_{-0{,}5}$ ist $\vec u=\begin{pmatrix}-0{,}5 \\ -1 \\ 0\end{pmatrix}$ und der Richtungsvektor von $g$ ist $\vec v=\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$ . Für den Schnittwinkel gilt dann:

$\displaystyle \cos \alpha$	$=$	$\displaystyle \dfrac{\|\vec u\circ \vec v\|}{\|\vec u\|\cdot \|\vec v\|}$
	$=$	$\displaystyle \dfrac{\left\|\begin{pmatrix}-0{,}5 \\ -1 \\ 0\end{pmatrix}\circ \begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}\right\|}{\sqrt{(-0{,}5)^2+(-1)^2+0^2}\cdot \sqrt{1^2+2^2+1^2}}$
	↓	Berechne das Skalarprodukt.
	$=$	$\displaystyle \dfrac{\left\|-0{,}5-2\right\|}{\sqrt{1{,}25}\cdot \sqrt{6}}$
	↓	Berechne den Betrag.
	$=$	$\displaystyle \dfrac{2{,}5}{\sqrt{7{,}5}}$

$\alpha=\cos^{-1}\left(\dfrac{2{,}5}{\sqrt{7{,}5}}\right)\approx24{,}1^\circ$

Der Schnittwinkel zwischen den beiden Geraden beträgt rund $24{,}1^\circ$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

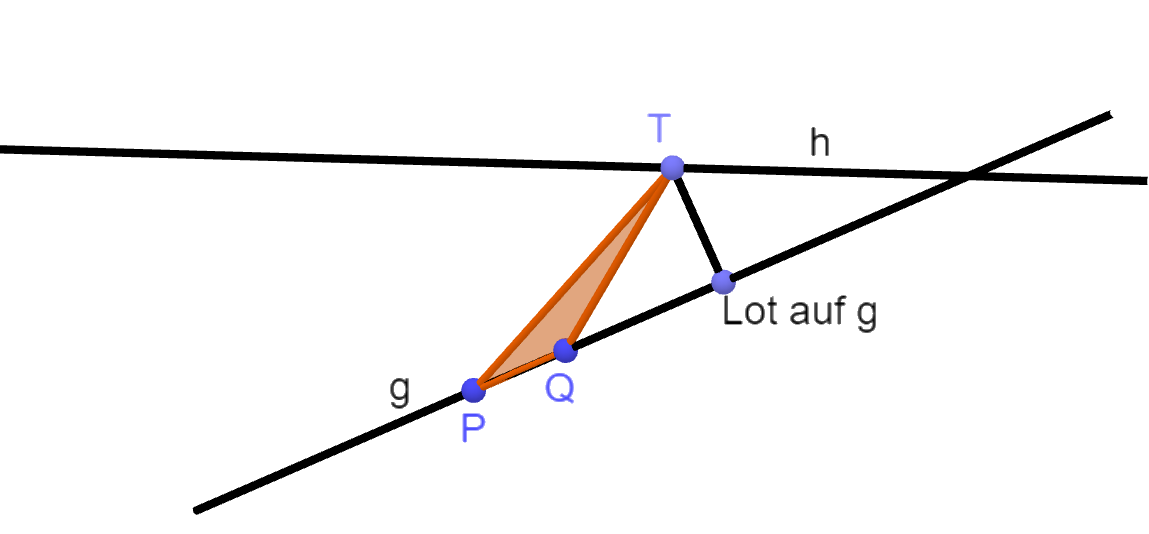
Der Punkt $T$ bewegt sich auf der Geraden $h_{0}$ und bildet mit zwei Punkten $P$ und $Q$ auf der Geraden $g$ ein Dreieck.
Begründen Sie, dass es genau einen Punkt $T$ gibt, für den das Dreieck $P Q T$ minimalen Flächeninhalt hat. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand zweier Geraden
Begründung, dass es genau einen Punkt $T$ gibt, für den das Dreieck $P Q T$ minimalen Flächeninhalt hat
Der Punkt $T$ bewegt sich auf der Geraden $h_{0}$ . Zwei Punkte $P$ und $Q$ liegen auf der Geraden $g$ und bilden zusammen mit $T$ ein Dreieck. Die beiden Geraden $g$ und $h_{0}$ sind windschief.
Siehe Skizze:
Die Dreiecksfläche ist $A_{PQT}=\dfrac{1}{2}\cdot |\overline {PQ}|\cdot h$ .
Dabei ist die Höhe $h$ das Lot von $T$ auf $g$ .
Diese Höhe ist am kleinsten, wenn $T$ auf $h_{0}$ dort liegt, wo sich $g$ und $h_{0}$ am nächsten sind. Das ist dann der Fall, wenn der Abstand von $T$ und $g$ genauso groß wie der Abstand von $g$ und $h_{0}$ ist.
In diesem Fall hat das Dreieck $P Q T$ einen minimalen Flächeninhalt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Dreiecksfläche ist $A_{PQT}=\dfrac{1}{2}\cdot |\overline {PQ}|\cdot h$ . Dabei ist die Höhe $h$ das Lot von $T$ auf $g$ .
Suche einen Ort für den Punkt $T$ auf $h_{0}$ , an dem die Höhe $h$ minimal wird.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle (3+r\cdot a)+2\cdot(4-r)+(4+r\cdot0)$	$=$	$\displaystyle 7$
	↓	Löse die Klammern auf
$\displaystyle 3+ra+8-2r+4$	$=$	$\displaystyle 7$
	↓	Fasse zusammen.
$\displaystyle 15+r(a-2)$	$=$	$\displaystyle 7$	$\displaystyle -15$
$\displaystyle r(a-2)$	$=$	$\displaystyle -8$	$\displaystyle :(a-2)$
$\displaystyle r$	$=$	$\displaystyle \dfrac{-8}{a-2}$
	↓	Klammere im Zähler und Nenner $(- 1)$ aus und kürze.
$\displaystyle r$	$=$	$\displaystyle \dfrac{8}{2-a}$

Aufgabe 3C

$A$ ist ein Punkt von $g$

Gleichung für $E$

Hast du eine Frage oder Feedback?

Gleichung der Ebene $H$ an, in der alle Geraden $h_{a}$ liegen

Nicht jeder Punkt der Ebene $H$ ist auch ein Punkt von $h_{a}$

Hast du eine Frage oder Feedback?

Gerade in Ebene einsetzen

Parameter untersuchen

Hast du eine Frage oder Feedback?

Schnittpunkt von $h_{a}$ mit g

Berechnen Sie den Schnittwinkel von $h_{-0{,}5}$ mit g

Hast du eine Frage oder Feedback?

Begründung, dass es genau einen Punkt $T$ gibt, für den das Dreieck $P Q T$ minimalen Flächeninhalt hat

Hast du eine Frage oder Feedback?

Aufgabe 3C

AAA ist ein Punkt von ggg

Gleichung für EEE

Hast du eine Frage oder Feedback?

Gleichung der Ebene HHH an, in der alle Geraden hah_{a}ha​ liegen

Nicht jeder Punkt der Ebene HHH ist auch ein Punkt von hah_{a}ha​

Hast du eine Frage oder Feedback?

Gerade in Ebene einsetzen

Parameter untersuchen

Hast du eine Frage oder Feedback?

Schnittpunkt von hah_{a}ha​ mit g

Berechnen Sie den Schnittwinkel von h−0,5h_{-0{,}5}h−0,5​ mit g

Hast du eine Frage oder Feedback?

Begründung, dass es genau einen Punkt TTT gibt, für den das Dreieck PQTP Q TPQT minimalen Flächeninhalt hat

Hast du eine Frage oder Feedback?

$A$ ist ein Punkt von $g$

Gleichung für $E$

Gleichung der Ebene $H$ an, in der alle Geraden $h_{a}$ liegen

Nicht jeder Punkt der Ebene $H$ ist auch ein Punkt von $h_{a}$

Schnittpunkt von $h_{a}$ mit g

Berechnen Sie den Schnittwinkel von $h_{-0{,}5}$ mit g

Begründung, dass es genau einen Punkt $T$ gibt, für den das Dreieck $P Q T$ minimalen Flächeninhalt hat