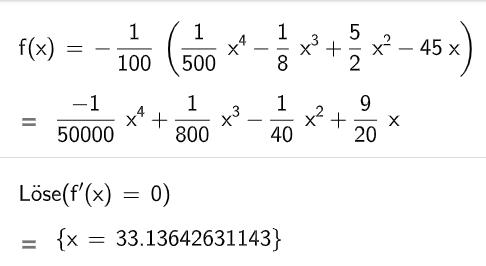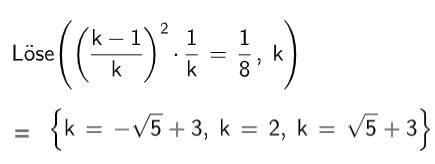Abiturprüfungen Mathe eA mit Lösungen

Aufgabe 1A

Die auf $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=5 \cdot\left(e^{-0{,}3 x}-e^{-4 x}\right)$ modelliert für $0 \leq x \leq 12$ die Konzentration eines Medikamentenwirkstoffes im Blut. Dabei beschreibt $x$ die Zeit in Stunden $(h)$ nach der Einnahme des Medikamentes und $f(x)$ die Konzentration in Milligramm pro Liter $\left(\frac{m g}{l}\right)$ .

Berechnen Sie die Konzentration eine Stunde nach der Einnahme des Medikamentes. Geben Sie den Zeitpunkt an, zu dem die Konzentration erstmals den Wert 2,8 $\frac{m g}{l}$ annimmt.
Bestimmen Sie, wie lange die Konzentration mindestens $0{,}5 \frac{\mathrm{mg}}{\mathrm{l}}$ beträgt. (6 BE)
Gib zunächst den Term in deinen CAS-Rechner ein.
Konzentration nach einer Stunde
Bestimme mithilfe des Rechners den Funktionswert einfach durch Einsetzen:
$f(1)\approx 3{,}6$
Somit beträgt die Konzentration nach einer Stunde noch $3{,}6 \frac{mg}{l}$
Konzentration übersteigt 2,8 $\frac {mg}{l}$
Verwende den "Löse"-Befehl (nSolve), um herauszufinden, wann $f(x)=2{,}8$ ist.
Der CAS liefert $x\approx 0{,}25$ und $x\approx1{,}93$ .
Dabei ist x in Stunden angegeben.
Da nach dem erstmaligen Überschreiten des Wertes gefragt ist, nimmst du den kleineren x-Wert als Lösung und rundest sinnvoll:
0,25 Stunden sind $0{,}25\cdot60=15$ Minuten.
Also wird der Wert erstmals nach ca 15 Minuten überschritten.
Konzentration mindestens $0{,}5\frac{mg}{l}$
Verwende erneut den "Löse"-Befehl (nSolve), um herauszufinden, wann $f(x)=0{,}5$ . Notiere dir diesmal beide Lösungen.
$x\approx 0{,}03$ und $x\approx 7{,}68$ (erneut in Stunden)
Um herauszufinden, wie lange die Konzentration im Blut mindestens $0{,}5\frac{mg}l$ beträgt, subtrahierst du die beiden Zeitpunkte voneinander:
$\Delta x=7{,}68-0{,}03=7{,}65$ .
Die Konzentration ist also für 7,6 Stunden höher als $0{,}5 \frac{mg}l$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Aus der Angabe weißt du:
$x$ : vergangene Zeit in Stunden seit der Einnahme
$f(x):$ vorhandene Konzentration in $\frac{mg}{l}$
Berechne den Funktionswert, indem du den x-Wert für eine Stunde einsetzt.
Berechne den x-Wert, indem du den Term mit dem Wert 2,8 gleichsetzt und die Gleichung löst.
Bestimme die Zeitpunkte, an denen die Funktion den Funktionswert 0,5 annimmt. Anschließend musst du aus den beiden Zeitpunkten eine Zeitspanne machen, indem du die Werte subtrahierst.
Zeigen Sie rechnerisch, dass die Konzentration ungefähr 0,7 Stunden nach der
Einnahme des Medikamentes mit etwa 3,75 $\frac{m g}{l}$ am größten ist. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
x-Koordinate der Extremstelle
Du kannst im ersten Schritt die Ableitungsfunktion mithilfe des CAS bestimmen:
$f'(x)=0{,}5(40e^{-4x}-3e^{-0{,}3x})$
Anschließend bestimmst du mit dem Löse-Befehl die Lösungen der Gleichung $f'(x)=0$
Wie in der Aufgabenstellung angegeben, erhältst du $x\approx0{,}7$ .
Art der Extremstelle
Bilde die zweite Ableitung:
$f''(x)=\frac 1 {20}(-1600e^{-4x}+9e^{-0{,}3x})$
Setze den soeben gefundenen Wert $x=0{,}7$ ein:
$f''(0{,}7)\approx -4{,}5$
Da der zugehörige Wert der 2. Ableitung negativ ist, hat der Graph von f bei $x=0{,}7$ einen Hochpunkt.
y-Koordinate bzw. zugehörige Konzentration
Setze zum Schluss noch $x=0{,}7$ in die Funktion $f$ ein, um die angegebene Konzentration im Blut zu überprüfen:
$f(0{,}7)\approx 3{,}75$
Die Konzentration ist nach rund $0{,}7$ Stunden mit etwa $375\;\frac{m g}{l}$ am höchsten.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme mithilfe des CAS-Rechners den Extrempunkt des Graphen:
Bestimme die Ableitung $f'$
Bestimme die Nullstellen der Ableitung $f'(x)=0$
Bestimme die Art der gefundenen Extremstelle mithilfe der zweiten Ableitung:
Bilde die zweite Ableitung $f''$
Setze den soeben gefundenen x-Wert in $f''$ ein
Überprüfe den zugehörigen y-Wert, indem du den x-Wert auch in $f$ einsetzt.
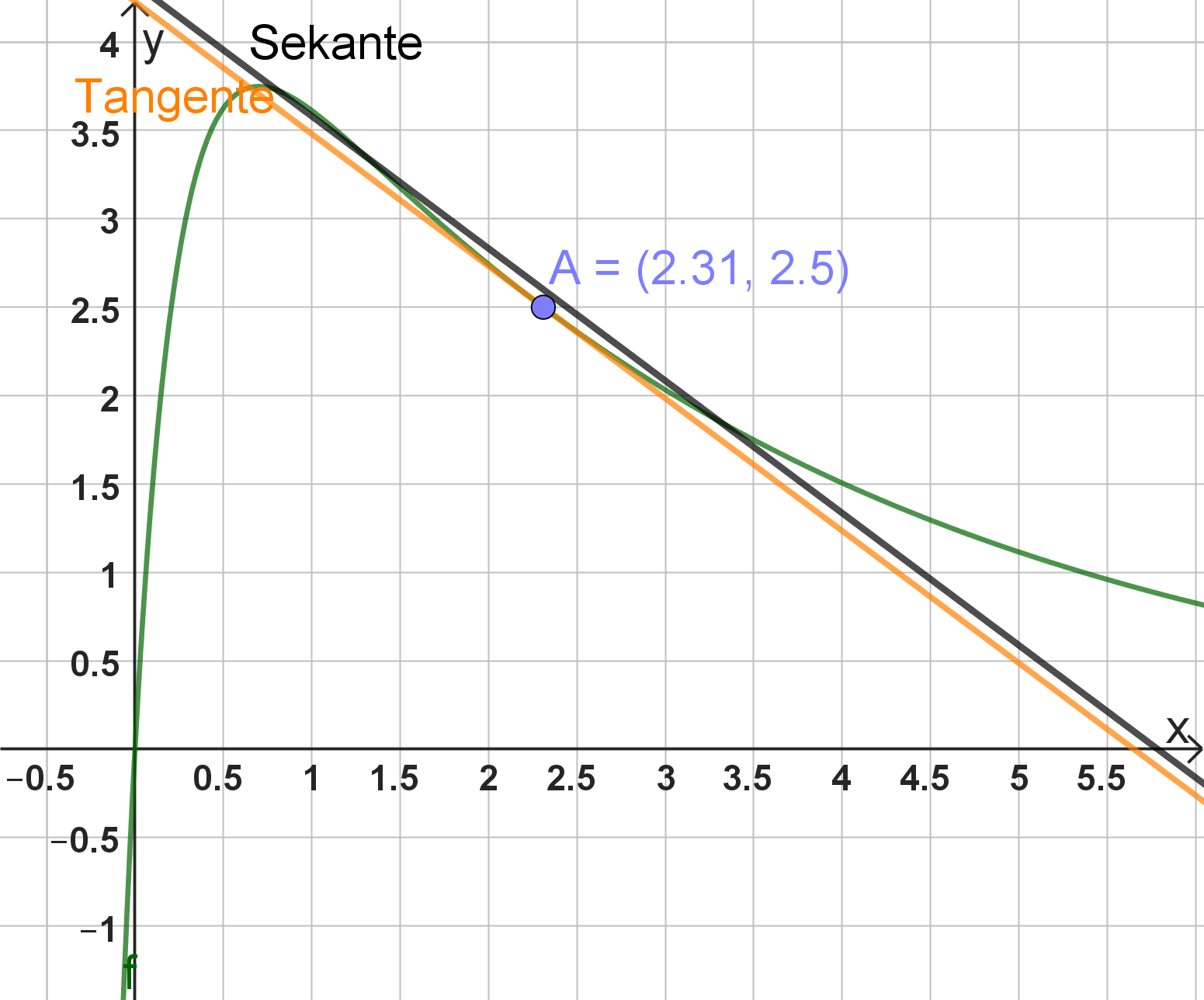
Berechnen Sie den Zeitpunkt, zu dem die Konzentration genau so groß ist wie zwei Stunden später. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Berechnung des x-Wertes
Sei $x_0$ ein beliebiger Startzeitpunkt. Dann ist gesucht, wann der Wert, der zwei Stunden nach $x_0$ angenommen wird, genauso groß ist wie der von $x_0:$
Der CAS-Rechner liefert $x\approx 0{,}22$
Also nach 0,2 Stunden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Verwende den CAS-Rechner, um den Zeitpunkt $x_0$ herauszufinden, bei dem $f(x_0)$ und $f(x_0+2)$ übereinstimmen.
Bestimmen Sie die Lösung der Gleichung $f^{\prime}(x)=\frac{f(x+1)-f(x-1)}{2}$ und interpretieren Sie die Lösung im Sachzusammenhang. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Differenzenquotient
Der CAS-Rechner liefert nach dem Löse-Befehl (nSolve) für $f'(x)=\frac{f(x+1)-f(x-1)}2$ : $x\approx 2{,}3$
Die Ableitungsfunktion $f'$ beschreibt die (Tangenten-)Steigung einer Funktion an einem ausgewählten x-Wert.
Der Bruch auf der rechten Seite ist ein Differenzenquotient: Es wird die durchschnittliche Steigung (Sekantensteigung) zwischen zwei x-Werten bestimmt, von denen einer um eins größer ist als der gerade betrachtete x-Wert und einer um eins kleiner.
In der Abbildung unten siehst du die graphische Interpretation: Gesucht ist der Punkt, an dem die Tangentensteigung genau so groß ist wie die oben definierte Sekantensteigung.
Skizze der Graphen
Deuten solltest du die Gleichung aber auch im Sachkontext:
2,3 Stunden nach der Einnahme ist die durchschnittliche Abnahme der Konzentration im Zeitraum zwischen 1,3 und 3,3 Stunden genau so groß wie die tatsächliche, momentane Abnahme der Konzentration.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Besimme zunächst die Lösung der Gleichung mit dem CAS-Rechner.
Zur Interpretation musst du dich an den Differenzenquotient (bzw. die Sekantensteigung) und die Bedeutung der Ableitungsfunktion erinnern.
Eine vereinfachte Modellierung geht davon aus, dass bis 6 Stunden nach der Einnahme des Medikamentes die Konzentration durch $f$ beschrieben wird und danach die Abnahmerate der Konzentration konstant ist. Dabei ist die konstante Abnahmerate so groß wie die Änderungsrate der durch $f$ beschriebenen Konzentration nach 6 Stunden.
Berechnen Sie den Zeitpunkt nach der Einnahme des Medikamentes, zu dem die Konzentration nach diesem Modell null ist. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Tangente bestimmen
Da der Graph an der Stelle $x=6$ stetig fortgesetzt werden soll, muss die Gerade, die daran anschließt, die gleiche Steigung haben. Es handelt sich also um die Tangente im Punkt $P(6|f(6))$ .
Du kannst die Tangente im CAS-Rechner bestimmen, zur Kontrolle hier aber das Ergebnis Schritt für Schritt berechnet:
$m=f'(6)\approx-0{,}25$ (gleiche Steigung)
und
$f(6)\approx 0{,}83$ (gleicher Funktionswert).
Also ist die Tangente in Punkt-Steigungs-Form:
$y=-0{,}25(x-6)+0{,}83$
bzw.
$y=-0{,}25x+2{,}33$
Nullstelle der Tangente
Bestimme im CAS-Rechner die Nullstelle der Tangente, indem du die Lösung der Gleichung $-0{,}25x+2{,}33=0$ bestimmst oder berechne sie durch Umformen selbst.
Du erhältst: $x\approx 9{,}3$
Also sinkt die Konzentration $9{,}3$ Stunden nach der Einnahme auf $0\;\frac{mg}l$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme zunächst die Tangente am Graphen im Punkt $P(6|f(6))$ . Vielleicht kann das dein CAS-Rechner, sonst benötigst du die Steigung an dieser Stelle ( $f'(6)=0$ ) und den Funktionswert $(f(6))$ .
Bestimme dann die Nullstelle der Tangente.
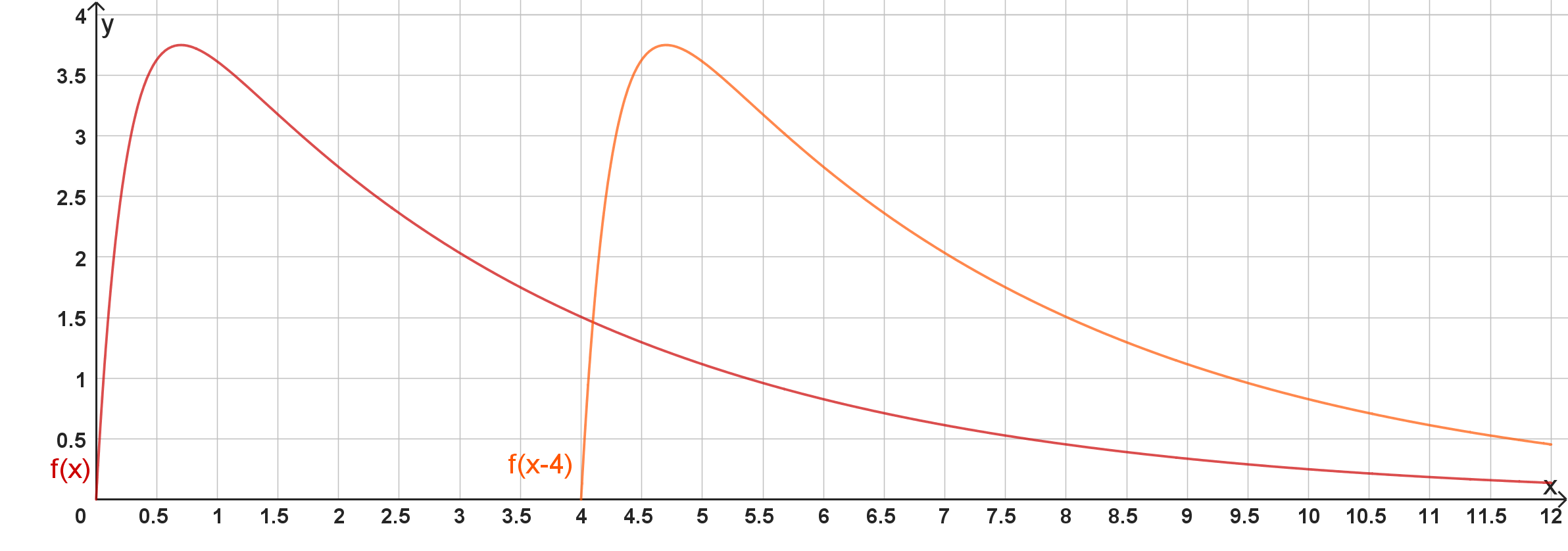
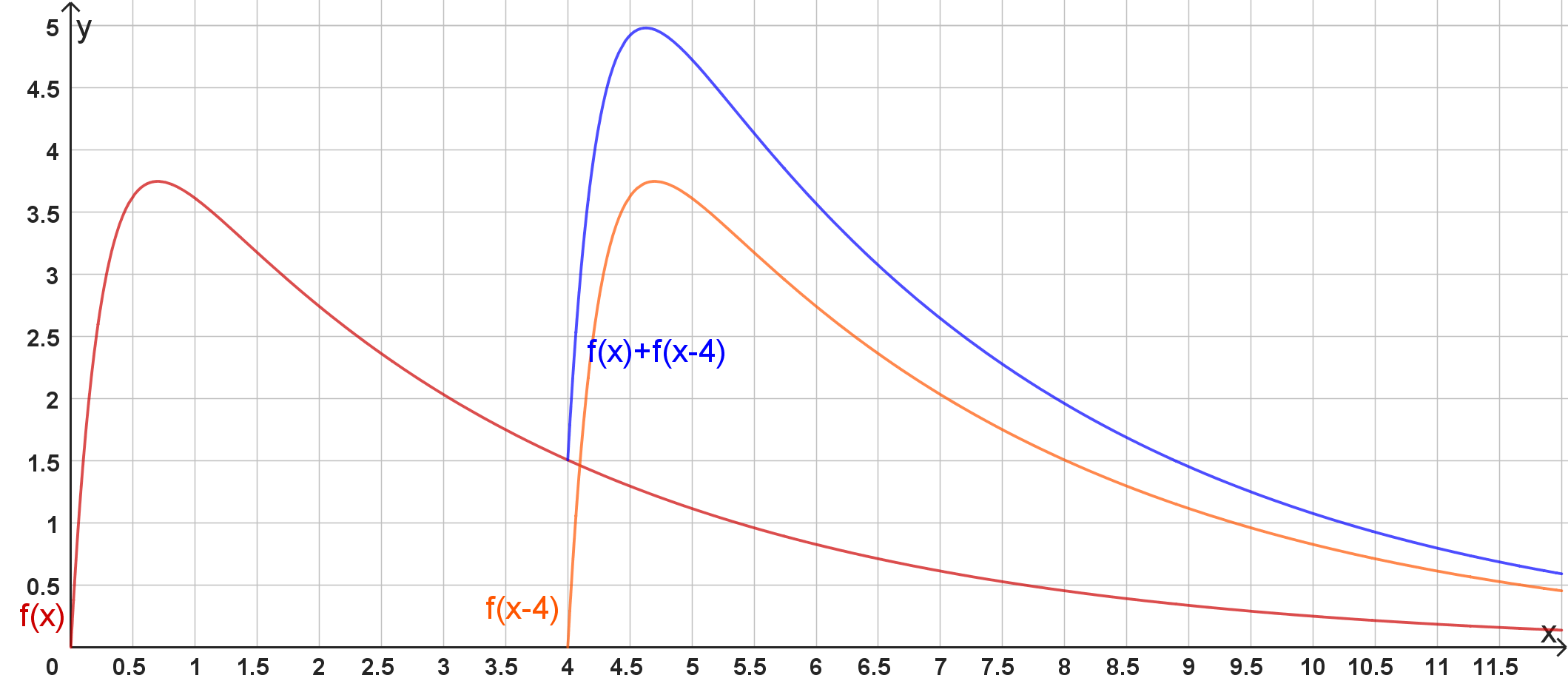
Vier Stunden nach der ersten Einnahme wird das Medikament in der gleichen Dosierung erneut eingenommen. Die Gesamtkonzentration ist zu jedem Zeitpunkt die Summe der durch $f$ beschriebenen Konzentrationen, die sich aus der ersten und zweiten Einnahme ergeben. Die Gesamtkonzentration soll $6 \frac{\mathrm{mg}}{\mathrm{l}}$ nicht übersteigen.
Untersuchen Sie, ob diese Vorgabe eingehalten wird. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Aus einer früheren Teilaufgabe weißt du, dass die höchste Konzentration 3,75 $\frac{mg}{l}$
Term für die Einnahme der zweiten Tablette
Durch $f(x-4)$ wird der Graph der Funktion f um vier nach rechts verschoben:
Darstellung der Graphen
Das allein genügt jedoch nicht, denn die bereits vorhandene Menge im Blut muss ebenfalls berücksichtigt werden. Diese muss dazuaddiert werden:
$f(x)+f(x-4)$
Darstellung der Graphen
Hochpunkt des neuen Funktionsgraphen
Bestimme mithilfe des CAS-Rechners die Extremstellen der neuen Hilfs-Funktion $h(x)=f(x)+f(x-4):$
$h'(x)=5(4e^{-4x}-0{,}3e^{-0{,}3x})+5(4e^{-4(x-4)}-0{,}3e^{-0{,}3(x-4)})$
Bestimme die Nullstellen der Ableitung:
$h'(x)=0$ für $x\approx4{,}63$
Bestimme die Art, indem du den Wert in die zweite Ableitung einsetzt:
$h''(4{,}63)<0$ also liegt ein Hochpunkt vor.
Bestimme den zugehörigen Funktionswert:
$h(4{,}63)\approx 4{,}98$
Die höchste Konzentration ist mit $4{,}98 \;\frac{mg}{l}$ unter dem vorgegebenen Höchstwert.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Untersuche, wie sich der Term verändert:
Statt bei $x=0$ zu starten, musst du bei $x=4$ starten, den Graphen also um 4 nach rechts verschieben
Außerdem musst du aber die noch vorhandene Restmenge von der ersten Tablette dazurechnen. Addiere den Term aus dem ersten Schritt zum Term der Ausgangsfunktion
Von dieser neuen Hilfsfunktion kannst du dann die Extremstelle und die zugehörige Konzentration bestimmen:
Bestimme die Ableitung
Bestimme die Nullstellen der Ableitung
Weise mit der 2. Ableitung nach, dass es sich um einen Hochpunkt handelt
Setze die gefundenen Nullstellen in die Hilfsfunktion ein und prüfe, ob der Wert kleiner als 6 $\frac{mg}l$ ist
Unabhängig vom Sachzusammenhang ist die Funktionenschar $f_{a}$ mit $f_{a}(x)=e^{-a \cdot x}-e^{-4 x}, x \in \mathbb{R}, a>0, a \neq 4$ , gegeben. In der Abbildung sind zwei Graphen der Schar dargestellt. Jeder Graph der Funktionenschar hat genau einen Extrempunkt.
Berechnen Sie die Werte von $a$ , für die die Fläche zwischen dem Graph von $f_{a}$ und der $x$ -Achse im Intervall $[0 ; 1]$ den Inhalt 0,2 hat. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Integral bestimmen
Nachdem du den Term mit dem Parameter $a$ eingegeben hast, kannst du das Integral im Bereich $[0;1]$ bestimmen und als Hilfsfunktion benennen:
Gleichung aufstellen und lösen
Du suchst die Werte von $a,$ für die der Betrag des Integrals gleich $0{,}2$ ist.
Löse die folgende Gleichung: $h(x)=0{,}2$
Du findest die beiden Werte $a_1\approx 1{,}9$ und $a_2\approx22{,}0$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Gib den neuen Term in den CAS-Rechner ein.
Bestimme das Integral im Bereich $[0;1]$ .
Setze das Ergebnis in Betragsstriche.
Bestimme, wann der Wert $0{,}2$ angenommen wird.

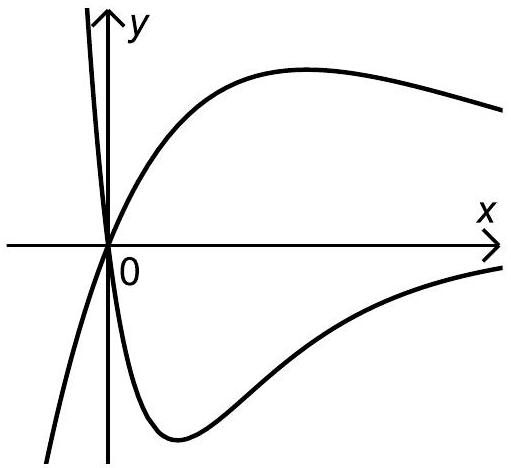
Entscheiden Sie, für welche Werte von $a$ an der Extremstelle ein Maximum und für welche ein Minimum vorliegt.

Begründen Sie Ihre Entscheidung ohne Berechnung der Extremstelle. (6 BE)

Extrema in Abhängigkeit von $a$

Aus der Abbildung in Teilaufgabe (g) erkennst du, dass es Graphen mit einem Tiefpunkt und Graphen mit einem Hochpunkt gibt.

Graphen mit einem Hochpunkt sind für $x>0$ oberhalb der x-Achse.

Graphen mit einem Tiefpunkt sind für $x>0$ unterhalb der x-Achse.

Der Funktionsterm nimmt für $x>0$ Werte in Abhängigkeit von $a$ an.

Die Terme $e^{-ax}$ und $e^{-4x}$ können mit dem Potenzgesetz umgeformt und verglichen werden, um herauszufinden, wann diese Fälle eintreten.

$\displaystyle e^{-ax}$	$=$	$\displaystyle e^{-4x}$
$\displaystyle (\frac{1}{e^{a}})^x$	$=$	$\displaystyle (\frac{1}{e^{4}})^x$
$\displaystyle \text{Beispiel für a>4: }~~~(\frac{1}{e^{8}})^x$	$<$	$\displaystyle (\frac{1}{e^{4}})^x~\text{weil }e^8>e^4$
$\displaystyle \text{Beispiel für 0<a<4: }~~~(\frac{1}{e^{2}})^x$	$>$	$\displaystyle (\frac{1}{e^{4}})^x~\text{weil }e^2<e^4$

Für $a=4$ wären die Terme gleich.

Also untersuchen wir zwei Fälle mit dem Funktionsterm:

$0<a<4$ , dann gilt für $x>0$ : $f_a(x)=\underbrace{e^{-a\cdot x}}_{\text{für a<4 größer als der andere Term}}-e^{-4x}>0$

$a>4$ , dann gilt für $x>0$ : $f_a(x)=\underbrace{e^{-a\cdot x}}_{\text{für a>4 kleiner als der andere Term}}-e^{-4x}<0$

Der erste Fall beschreibt Graphen mit einem Hochpunkt, der zweite Fall Graphen mit einem Tiefpunkt, siehe Abbildung.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Der Graph von $f_{a}$ wird an der $x$ -Achse gespiegelt.

Berechnen Sie die Werte von $a$ , für die sich der gespiegelte Graph und der Graph von $f_{a}$ unter einem rechten Winkel schneiden. (5 BE)

2

Aufgabe 1B

Gegeben ist die auf $\mathbb{R}$ definierte Funktionenschar $f_{a}$ mit $f_{a}(x)=x(x-a)(x-2 a), a \neq 0$

Geben Sie die Nullstellen des Graphen von $f_{3}$ an.

Berechnen Sie die Koordinaten des Hochpunktes des Graphen von $f_{3}$ . (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion mit Parameter

Nullstellen bestimmen

Ein Produkt ist genau dann $0$ , wenn einer der Faktoren gleich $0$ ist. Also gilt:

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Damit sind die Nullstellen: $x_1=0,\;x_2=3,\;x_3=6$

Funktion umformen

Um $f_a(x)$ leichter abzuleiten multiplizieren wir alle Klammern aus:

	$\displaystyle x\left(x-3\right)\left(x-6\right)$
$=$	$\displaystyle x\left(x^2-3x-6x+18\right)$
$=$	$\displaystyle x(x^2-9x+18)$
$=$	$\displaystyle x^3-9x^2+18x$

Ableitungen bilden

Mittels der Potenz- und Summenregel erhalten wir die ersten beiden Ableitungen:

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Hochpunkt berechnen

Alle Extremstellen sind auch Nullstellen der ersten Ableitung. Wir lösen also:

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Um dies zu lösen wenden wir die Mitternachtsformel mit $a=3$ , $b=-18$ und $c=18$ an und erhalten:

$\displaystyle x_{1{,}2}$	$=$	$\displaystyle \frac{18\pm\sqrt{18^2-4\cdot3\cdot18}}{2\cdot 3}$
	↓	Quadrate und Produkte ausrechnen
	$=$	$\displaystyle \frac{18\pm\sqrt{324-216}}{6}$
	↓	Die Summe auftrennen und kürzen
	$=$	$\displaystyle 3\pm\frac{\sqrt{108}}{6}$
	↓	Die $108$ faktorisieren
	$=$	$\displaystyle 3\pm\frac{\sqrt{3\cdot 36}}{6}$
	↓	Die $36$ aus der Wurzel ziehen und kürzen
	$=$	$\displaystyle 3\pm\sqrt{3}$

Wir setzen nun $x_{1{,}2}$ in $f_3''$ ein. Ist das Ergebnis negativ, so haben wir einen Hochpunkt gefunden:

$\displaystyle f_3''(x_{1{,}2})$	$=$	$\displaystyle 6(3\pm\sqrt{3})-18$
	$=$	$\displaystyle 18\pm6\sqrt{3}-18$
	$=$	$\displaystyle \pm6\sqrt3\overset{!}{<}0$

Da $6\sqrt{3}>0$ ist, ist der einzige Hochpunkt bei $x_H=3-\sqrt{3}$ . Nun rechnen wir noch die $y$ -Koordinate des Hochpunkts aus:

$\displaystyle f_3(x_H)$	$=$	$\displaystyle x_H(x_H-3)(x_H-6)$
	↓	Einsetzen und Summen ausrechnen
	$=$	$\displaystyle (3-\sqrt3)(-\sqrt{3})(-3-\sqrt3)$
	↓	3. Binomische Formel auf die 1. und 3. Klammer anwenden
	$=$	$\displaystyle -\sqrt{3}(-9+3)$
	↓	Summe ausrechnen
	$=$	$\displaystyle 6\sqrt3$

Also ist der Hochpunkt von $f_3$ bei $(3-\sqrt3\mid6\sqrt3)$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Bestimmen Sie den Wert von $a, a \neq 3$ , für den der zugehörige Graph von $f_{a}$ im Intervall $[-1 ; 0]$ dieselbe durchschnittliche Steigung hat wie der Graph von $f_{3}$ . (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Differenzenquotient

Erste Steigung

Um die durchschnittliche Steigung von $f_a$ im Intervall $[-1;0]$ zu finden, nutzen wir den Differenzenquotienten und erhalten:

$\displaystyle m_a$	$=$	$\displaystyle \frac{f_a(0)-f_a(-1)}{0-(-1)}$
	↓	Teilen durch $1$ weglassen
	$=$	$\displaystyle f_a(0)-f_a(-1)$
	↓	$0$ ist eine Nullstelle von $f_a$
	$=$	$\displaystyle -f_a(-1)$
	↓	Formel einsetzen
	$=$	$\displaystyle -(-1)(-1-a)(-1-2a)$
	↓	Aus allen Klammer ein Minus ausklammern
	$=$	$\displaystyle (1+a)(1+2a)$
	↓	Ausmultiplizieren.
	$=$	$\displaystyle 1+2a+a+2a^2$
	↓	Zusammenfassen
	$=$	$\displaystyle 2a^2+3a+1$

Zweite Steigung

Um die durchschnittliche Steigung von $f_3$ zu berechnen, setzen wir in die generelle Formel $a=3$ ein:

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Gleichsetzen

Wir setzen nun die beiden Steigung gleich und lösen nach $a$ :

$\displaystyle m_3$	$=$	$\displaystyle m_a$
$\displaystyle 28$	$=$	$\displaystyle 2a^2+3a+1$	$\displaystyle -28$
$\displaystyle 0$	$=$	$\displaystyle 2a^2+3a-27$

Um dies nach $a$ zu lösen, nutzen wir die Mitternachtsformel:

$\displaystyle a_{1{,}2}$	$=$	$\displaystyle \frac{-3\pm\sqrt{3^2-4\cdot2\cdot(-27)}}{2\cdot2}$
	↓	Potenzen und Produkte ausrechnen
	$=$	$\displaystyle \frac{-3\pm\sqrt{9+216}}{4}$
	↓	Summe ausrechnen
	$=$	$\displaystyle \frac{-3\pm\sqrt{225}}{4}$
	↓	Wurzel ausrechnen
	$=$	$\displaystyle \frac{-3\pm 15}{4}$

Also ist $a_1=\dfrac{12}{4}=3$ , was ein guter Konsistenzcheck ist. Damit ist der gesuchte Parameter: $a_2=-\dfrac{18}{4}=-4{,}5$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Begründen Sie, dass für jeden Wert von $a$ die Graphen zu $f_{a}$ und $f_{-a}$ im Koordinatenursprung dieselbe Tangente haben. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Ableitung
Wir formen zuerst $f_a$ um, damit wir die Ableitung leichter bilden können. Dazu multiplizieren wir alle Klammern aus:
Dann berechnen wir die Ableitung mit der Summen- und Potenzregel:
Parallelität
Die Steigung der Tangente zu $f_a$ bei $x=0$ ist $f_a'(0)$ . Dies können wir einfach ausrechnen: $m_a=f'_a(0)=2a^2$ . Analog ist die Steigung der Tangente zu $f_{-a}$ durch $f_{-a}'(0)$ gegeben:
Also haben beide Tangenten die gleiche Steigung, sind also parallel.
Identisch
Da $x=0$ eine Nullstelle von $f_a$ und von $f_{-a}$ ist, gilt $f_a(0)=0=f_{-a}(0)$ . Da die Tangenten zu $f_{\pm a}$ bei $x=0$ jeweils durch $f_{\pm a}(0)$ laufen, gehen beide durch den Punkt $(0\mid 0)$ . Insbesondere schneiden sich also beide Tangenten. Da sie außerdem parallel sind, müssen sie identisch sein.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bilde die Ableitung von $f_a$
Zeige, dass die Tangenten parallel sind
Begründe, warum die Tangenten identisch sein müssen

Zeigen Sie, dass für jeden Wert von $a$ der Graph zu $f_{a}$ durch eine Spiegelung am Punkt $(0|0)$ auf den Graphen von $f_{-a}$ abgebildet wird. (4 BE)

Betrachtet wird die Tangente an den Graphen von $f_{a}$ im Wendepunkt $(a \mid 0)$ .
Berechnen Sie die Werte von $a$ , für die diese Tangente mit den Koordinatenachsen ein gleichschenkliges Dreieck einschließt. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreieck
Beschreibung des Dreiecks
Da zwei der Seiten des Dreiecks auf den Koordinatenachsen liegen, ist es insbesondere ein rechtwinkliges Dreieck.
Da in einem gleichschenkligen Dreieck die zwei Basiswinkel gleich groß sein müssen, folgt mit der Innenwinkelsumme, dass die Basiswinkel 45 Grad groß sein müssen.
Steigung folgern
Wir wissen nun, dass die Tangente in einem Winkel von 45 Grad zu den Koordinatenachsen liegt. Die einzigen möglichen Steigungen sind damit $m=\pm1$ .
Parameter finden
Wir berechnen nun zuerst die Steigungen der Tangenten zu $f_a$ bei $x=a$ . Diese ist durch die Ableitung $f_a'(a)$ gegeben. Also gilt:
Wir wissen bereits, dass das Dreieck nur bei den Steigungen $m_{1{,}2}=\pm1$ gleichschenklig ist. Also setzen wir gleich und lösen nach $a$ :
Da Quadrate nicht negativ werden, kann der Fall $m=1$ nicht erreicht werden und wir lösen:
Also ist das gebildete Dreieck für $a=\pm1$ gleichschenklig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Überlege dir, wie dieses Dreieck aussieht
Folgere, welche Steigung die Tangenten haben muss
Löse nach dem Parameter $a$ auf

Berechnen Sie die Werte von $a$ , sodass die Fläche zwischen dem zugehörigen Graphen von $f_{a}$ und der $x$ -Achse im Intervall $[0 ; 2]$ den Inhalt 1 hat. (8 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen

Stammfunktion berechnen

Da wir im Laufe der Aufgabe das Integral von $f_a$ mehrfach ausrechnen müssen, berechnen wir die Stammfunktion einmal und wenden sie dann wiederholt an.

Zuerst multiplizieren wir $f_a$ aus und erhalten $f_a=x^3-3ax^2+2a^2x$ . Dann ist die Stammfunktion nach der Summen- und Potenzregel:

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Intervall auftrennen

Um die Fläche auszurechnen, müssen wir zuerst untersuchen, ob die Funktion im Intervall $]0;2[$ einen Vorzeichenwechsel hat. Da eine Funktion nur in Nullstellen ihr Vorzeichen wechseln kann, untersuchen wir die Nullstellen von $f_a$ .

Diese sind bei $x_1=0,x_2=a,x_3=2a$ .

Die verschiedenen Fälle sind also:

$a\leq0$ : Keine der Nullstellen liegt in $]0;2[$
$0<a<1$ : Die Nullstellen $a$ und $2a$ liegen in $]0;2[$
$1\leq a<2$ : Nur die Nullstelle $a$ liegt in $]0;2[$
$2\leq a$ : Keine der Nullstellen liegen in $]0;2[$

Da die anderen Fälle nicht leicht abzuschätzen sind, berechnen wir diese direkt.

Integrale berechnen

$0<a<1$ :

In diesem Fall trennen wir das Intervall zu $]0;a[\;\cup\;]a;2a[\;\cup\;]2a;2[$ auf. Dementsprechend müssen wir drei Integrale ausrechnen:

Also ist die Fläche im Fall $0<a<1$ :

$\displaystyle A_{0<a<1}$	$=$	$\displaystyle A_1+A_2+A_3$
	↓	Die Flächen müssen positiv sein
	$=$	$\displaystyle \|I_1\|+\|I_2\|+\|I_3\|$
	↓	Einsetzen
	$=$	$\displaystyle \frac{1}{4}a^4+\frac{1}{4}a^4+4(a-1)^2$
	↓	Zusammenfassen und die 2. Binomische Formel anwenden
	$=$	$\displaystyle \frac{1}{2}a^4+4(a^2-2a+1)$
	↓	Ausmultiplizieren
	$=$	$\displaystyle \frac{1}{2}a^4+4a^2-8a+4$

$1\leq a<2$ :

Wir trennen das Intervall zu $]0;a[\;\cap\;]a,2[$ auf.

Um nun die Fläche auszurechnen, müssen wir überprüfen, ob die Integrale positiv oder negativ sind. Das erste Integral ist offensichtlich nicht-negativ, da $a^4$ nicht-negativ ist. Das zweite Integral ist etwas komplizierter. Wir berechnen zuerst den Wert des Integrals für $a=1$ :

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Da wir unsere Intervalle so gewählt haben, dass die Funktion auf ihnen konstant negativ oder positiv ist, muss also $I_2'<0$ für das gesamte Intervall, also $1\leq a<2$ , gelten. Also ist:

$\displaystyle A$	$=$	$\displaystyle A_1'+A_2'$
	↓	Die Flächen müssen positiv sein
	$=$	$\displaystyle \|I_1'\|+\|I_2'\|$
	↓	Einsetzen der Integrale, wobei das zweite Integral invertiert werden muss
	$=$	$\displaystyle \frac{1}{4}a^4+\frac{1}{4}a^4-4a^2+8a-4$
	↓	Zusammenfassen
	$=$	$\displaystyle \frac{1}{2}a^4-4a^2+8a-4$

Lösen nach $a$

Wir setzen nun die Formeln der Fläche gleich $1$ und lösen nach $a$ . Da wir Polynome vom Grad $4$ nicht per Hand lösen können, lassen wir den Taschenrechner für uns rechnen. Nutze dazu den Befehl "nSolve".

Im ersten Fall liefert das: $a_1\approx 0{,}508$ und $a_2\approx 1{,}158$ .

Da wir im ersten Fall aber $0<a<1$ haben, ist der gesuchte Wert $a_1\approx 0{,}51$ .

Im zweiten Fall liefert der Rechner: $a_1\approx -3{,}629$ und $a_2\approx 1{,}267$ . Da wir hier $1\leq a<2$ haben, ist der gesuchte Wert $a_2\approx 1{,}27$ .

Also sind die Werte für $a$ , sodass die Fläche zwischen $f_a$ und der $x$ -Achse im Intervall $[0;2]$ die Größe $1$ hat: $a_1\approx 0{,}51$ und $a_2\approx 1{,}27$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Berechnen Sie die Koordinaten der Tiefpunkte der Graphen von $f_{a}$ . (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe

Ableitungen bilden

Wir multiplizieren die Funktion aus und berechnen die Ableitungen mit der Summen- und Potenzregel:

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Extremstellen finden

Extremstellen sind immer Nullstellen der ersten Ableitung. Diese Nullstellen finden wir mit der Mitternachtsformel:

Wir setzen die Werte für $a,b,c$ in die Mitternachtsformel ein
	↓
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle \frac{6a\pm\sqrt{36a^2-24a^2}}{6}$
	↓	Zusammenfassen und kürzen
	$=$	$\displaystyle a\pm\frac{\sqrt{12}a}{6}$
	↓	$12$ in Faktoren aufteilen
	$=$	$\displaystyle a\pm\frac{\sqrt{4\cdot 3}a}{6}$
	↓	Die $4$ aus der Wurzel ziehen
	$=$	$\displaystyle a\pm\frac{2\sqrt{3}a}{6}$
	↓	Kürzen und $\frac{\sqrt3}{3}=\frac{1}{\sqrt3}$
	$=$	$\displaystyle a\pm\frac{1}{\sqrt{3}}a$
$\displaystyle x_1$	$=$	$\displaystyle a+\frac{1}{\sqrt{3}}a$
$\displaystyle x_2$	$=$	$\displaystyle a-\frac{1}{\sqrt{3}}a$

Tiefpunkt finden

Bei einem Tiefpunkt ist die zweite Ableitung positiv. Wir setzen also unsere Extremstellen in $f_a''(x)$ ein und testen, ob $f''_a$ positiv ist.

$\displaystyle f_a''(x_1)$	$=$	$\displaystyle 6\left(a+\frac{a}{\sqrt{3}}\right)-6a$
	↓	Ausmultiplizieren
	$=$	$\displaystyle 6a+\frac{6}{\sqrt{3}}a-6a$
	↓	Zusammenfassen und kürzen
	$=$	$\displaystyle 2\sqrt{3}a$

Genau gleich erhält man für $f_a''(x_2)=-2\sqrt{3}a$

Für $a<0$ ist also $x_2$ die gesuchte Stelle, bei $a>0$ ist es $x_1$ .

Werte ausrechnen

Um die $y$ -Koordinaten auszurechnen, setzen wir $x_{1{,}2}$ in die Funktion ein:

$\displaystyle f_a(x_1)$	$=$	$\displaystyle \left(a+\frac{a}{\sqrt{3}}\right)\left(\left(a+\frac{a}{\sqrt{3}}\right)-a\right)\left(\left(a+\frac{a}{\sqrt{3}}\right)-2a\right)$
	↓	Zusammenfassen und $a$ ausklammern.
	$=$	$\displaystyle a^3\left(\frac{1}{\sqrt{3}}+1\right)\left(\frac{1}{\sqrt{3}}\right)\left(\frac{1}{\sqrt{3}}-1\right)$
	↓	3. Binomische Formel auf die äußeren Klammern anwenden
	$=$	$\displaystyle \frac{1}{\sqrt{3}}a^3\left(\frac{1}{3}-1\right)$
	↓	Zusammenfassen
	$=$	$\displaystyle -\frac{2}{3\sqrt{3}}a^3$

Für $f(x_2)$ ergibt der gleiche Rechenweg $f_a(x_2)=\frac{2}{3\sqrt{3}}a^3$ .

Also ist der Tiefpunkt von $f_a(x)$ bei $TP\left(a+\frac{a}{\sqrt{3}}\mid -\frac{2}{3\sqrt{3}}a^3\right)$ falls $a>0$ . Für $a<0$ liegt er bei $TP\left(a-\frac{a}{\sqrt{3}}\mid \frac{2}{3\sqrt{3}}a^3\right)$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Betrachtet wird nun die Funktion $f_{3}$ .

Die Tangente an den Graphen von $f_{3}$ im Tiefpunkt schließt mit dem Graphen von $f_{3}$ eine Fläche ein. Außerdem schließt der Graph von $f_{3}$ mit der $x$ -Achse im Intervall $[0 ; 3]$ eine Fläche ein.

Berechnen Sie das Verhältnis der Inhalte dieser beiden Flächen. (7 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen

Tangente finden

In der vorherigen Teilaufgabe haben wir bereits den Tiefpunkt von $f_a$ gefunden. Wir müssen also nur $a=3$ setzen und erhalten:

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Da die Stelle des Tiefpunkts eine Nullstelle der ersten Ableitung ist, ist die Steigung der Tangente einfach $0$ .

Da die Tangente durch den Tiefpunkt gehen muss, ist sie einfach die konstante Funktion: $t(x)=-6\sqrt{3}$ .

Schnittpunkte finden

Um die Schnittpunkte zu finden, setzen wir die Funktionen gleich:

$\displaystyle t(x)$	$=$	$\displaystyle f_3(x)$
	↓	Einsetzen
$\displaystyle -6\sqrt{3}$	$=$	$\displaystyle x^3-9x^2+18x$	$\displaystyle +6\sqrt{3}$
	↓	Alles auf eine Seite bringen
$\displaystyle 0$	$=$	$\displaystyle x^3-9x^2+18x+6\sqrt{3}$
	↓	Diese Gleichung kann der TR lösen. Alternativ kann mit der Polynomdivision von Hand weitergerechnet werden:
	$=$	$\displaystyle (x-(3+\sqrt{3}))\left(x^2-(6-\sqrt{3})x+(3-3\sqrt{3})\right)$

Erste Fläche berechnen

$\displaystyle I_1$	$=$	$\displaystyle \int_{x_2}^{x_1}f_3(x)-t(x)\;dx$
	$=$	$\displaystyle \int_{3-2\sqrt{3}}^{3+\sqrt{3}}x^3-9x^2+18x+6\sqrt{3}\;dx$
	$=$	$\displaystyle \left[\frac{1}{4}x^4-3x^3+9x^2+6\sqrt{3}x\right]_{3-2\sqrt{3}}^{3+\sqrt{3}}$
	↓	TR
	$=$	$\displaystyle \frac{243}{4}$

Zweite Fläche berechnen

Da die Nullstellen von $f_3$ nicht im Intervall $]0{,}3[$ liegen, müssen wir das Integral nicht auftrennen.

$\displaystyle A_2$	$=$	$\displaystyle \int_0^3f_3(x)dx$
	$=$	$\displaystyle \left[\frac{1}{4}x^4-3x^3+9x^2\right]_0^3$
	$=$	$\displaystyle \frac{81}{4}-3\cdot27+9\cdot9$
	$=$	$\displaystyle \frac{81}{4}$

Verhältnis ausrechnen

Das Verhältnis ist:

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Also ist die Fläche zwischen $f_3$ und $t$ $3$ -mal so groß, wie die Fläche unter $f_3$ im Intervall $[0{,}3]$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

3

Aufgabe 1C

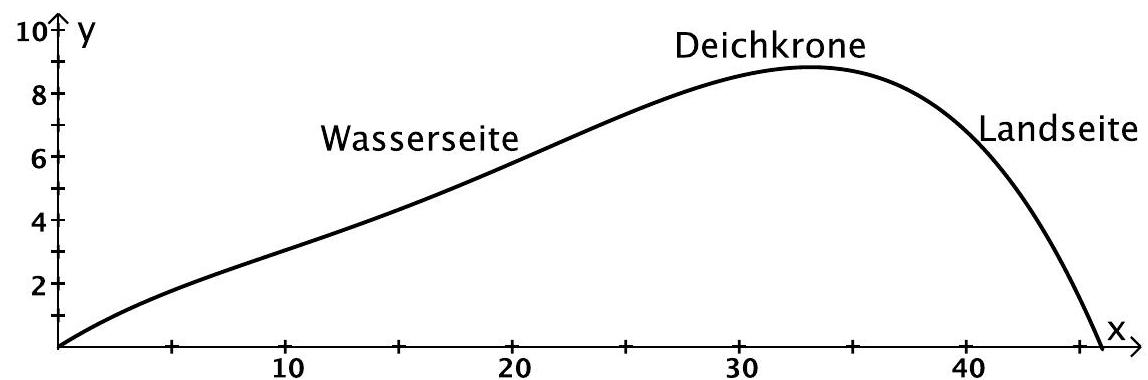
Gegeben ist die auf $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=-\frac{1}{100} \cdot\left(\frac{1}{500} x^{4}-\frac{1}{8} x^{3}+\frac{5}{2} x^{2}-45 x\right)$ . Im Küstenschutz ist ein neuer Deich von Bedeutung: der Klimadeich. Der Querschnitt eines Klimadeiches wird durch die von dem Graphen der Funktion $f$ und der $x$ -Achse eingeschlossenen Fläche modelliert. Dabei werden $x$ und $f(x)$ in Metern $(m)$ angegeben.

Die Abbildung zeigt den Graphen von $f$ . Markieren Sie auf der $x$ -Achse das Intervall, in dem der Klimadeich mindestens $5 \mathrm{~m}$ hoch ist.
Ein moderner Deich ist etwa fünfmal so breit wie er hoch ist.
Entscheiden Sie, ob der Klimadeich diese Regel erfüllt.
Begründen Sie Ihre Entscheidung nur mithilfe der Abbildung. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Intervall, in dem der Klimadeich mindestens $5 \mathrm{~m}$ hoch ist
Zeichne eine Parallele zur x-Achse im Abstand $5$ . Betrachte die x-Koordinaten der beiden Schnittpunkte der Parallelen mit dem Graphen von $f$ .
Dann gehen die Markierung auf der x-Achse von etwa $17$ bis etwa $42$ .

Entscheidung, ob der Klimadeich diese Regel (etwa fünfmal so breit wie er hoch) erfüllt
Die beiden Nullstellen von $f$ liegen bei $x=0$ und bei $x\approx46$ , d.h. der Deich hat eine Breite von etwa $46\;\text{m}$ . Die y-Koordinate des Maximums ist die Dammhöhe. Sie beträgt etwa $9\;\text{m}$ .
$\;\Rightarrow\;\dfrac{46}{9}\approx5$
Der Klimadeich erfüllt diese Regel.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Zeichne eine Parallele im Abstand $5$ zur x-Achse ein.
Betrachte die x-Koordinaten der beiden Schnittpunkte der Parallelen mit dem Graphen von $f$ .
Teil 2
Die Differenz der beiden Nullstellen ergibt die Breite des Damms. Die y-Koordinate des Maximums ist die Dammhöhe. Bilde den Quotienten.
Die maximale Höhe des Klimadeiches ist 0,9 $\mathrm{m}$ höher als die des zuvor vorhandenen Deiches.
Berechnen Sie die maximale Höhe des früheren Deiches auf $\mathrm{cm}$ genau. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Maximale Höhe des früheren Deiches auf $\mathrm{cm}$ genau
Berechne $f'(x)=0$ :
GeoGebra-TR
An der Stelle $x\approx 33{,}14$ liegt das Maximum der Funktion $f$ vor.
$f(33{,}14)$ ist die maximale Höhe des Deiches.
$f(33{,}14)=-\frac{1}{100} \cdot\left(\frac{1}{500}\cdot 33{,}14^{4}-\frac{1}{8} \cdot33{,}14^{3}+\frac{5}{2}\cdot 33{,}14^{2}-45\cdot 33{,}14\right)\approx8{,}83$
Die Höhe des früheren Deiches ist dann:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $f'(x)=0$ $\;\Rightarrow\; x_1$ (Stelle des höchsten Punkts).
Deichhöhe des Klimadeiches: Berechne $f(x_1)$ .
Höhe des früheren Deiches: Berechne $f(x_1)-0{,}9$ .
Berechnen Sie die durchschnittliche Steigung des Klimadeiches im Intervall $[0; 30]$ .
Berechnen Sie den Neigungswinkel des Klimadeiches an der Stelle $x=0$ . (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung und Steigungswinkel
Durchschnittliche Steigung des Klimadeiches im Intervall $[0; 30]$
Durchschnittliche Steigung $=\dfrac{f(30)-f(0)}{30-0}$
Mit $f(30)=\dfrac{171}{20}$ und $f(0)=0$ folgt dann:
Durchschnittliche Steigung $=\dfrac{\frac{171}{20}-0}{30}=\dfrac{57}{200}=0{,}285$
Die durchschnittliche Steigung des Klimadeiches im Intervall $[0; 30]$ beträgt $0{,}285$ .
Neigungswinkel des Klimadeiches an der Stelle $x=0$
Es ist $f'(0)=\dfrac{9}{20}$ .
Dann gilt für den Neigungswinkel des Klimadeiches:
Der Neigungswinkel des Klimadeiches an der Stelle $x=0$ beträgt rund $24^\circ$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Die durchschnittliche Steigung beträgt $\dfrac{f(30)-f(0)}{30-0}$ .
Teil2
Berechne $f'(0)\;\Rightarrow\alpha=\tan^{-1}\left(f'(0)\right)$ .
Der Klimadeich besteht aus einem Sandkern und einer Abdeckungsschicht aus Kleiboden. Im Querschnitt hat die Abdeckungsschicht aus Kleiboden im Bereich $5 \leq x \leq 42$ an jeder Stelle eine vertikale Dicke von $1{,}5 \mathrm{~m}$ .
Berechnen Sie den prozentualen Anteil des Sandkerns im Querschnitt im Bereich $5 \leq x \leq 42$ . (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Prozentualer Anteil des Sandkerns im Querschnitt im Bereich $5 \leq x \leq 42$
Oberer Randverlauf des Sandkerns: $g(x)=f(x)-1{,}5$
Inhalt des Querschnitts: $A_Q=\displaystyle\int_5^{42}f(x)\;dx\approx224{,}37$
Inhalt des Sandkernquerschnitts: $A_S=\displaystyle\int_5^{42}g(x)\;dx\approx168{,}97$
Dann gilt für das Verhältnis: $\quad\dfrac{A_S}{A_Q}=\dfrac{168{,}97}{224{,}37}\approx0{,}753$
Der prozentuale Anteil des Sandkerns im Querschnitt im Bereich $5 \leq x \leq 42$ beträgt rund $75\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der obere Randverlauf des Sandkerns wird durch $g(x)=f(x)-1{,}5$ beschrieben.
Berechne jeweils mit einem Integral die beiden Flächeninhalte über $f(x)$ und $g(x)$ von $5$ bis $42$ und bilde dann den Quotienten der beiden Flächeninhalte.
Begründen Sie, dass im Bereich von $a$ bis $b$ mit $5 \leq a<b \leq 42$ der Inhalt des
Querschnitts der Kleibodenschicht mit $1{,}5\cdot(b-a)$ berechnet werden kann. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Querschnitts der Kleibodenschicht kann mit $1{,}5\cdot(b-a)$ berechnet werden
Der untere Rand der Kleibodenschicht ist gegeben durch $g(x)=f(x)-1{,}5$ .
Der Flächeninhalt des Querschnitts der Kleibodenschicht ist: $\displaystyle\int_a^{b}\left(f(x)-g(x)\right)\;dx=\displaystyle\int_a^{b}(f(x)-(f(x)-1{,}5))\;dx=\displaystyle\int_a^{b}1{,}5\;dx$
$\displaystyle\int_a^{b}1{,}5\;dx=[1{,}5x]_a^b=1{,}5\cdot(b-a)$
Damit ist gezeigt, dass der Inhalt des Querschnitts der Kleibodenschicht mit $1{,}5\cdot(b-a)$ berechnet werden kann.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der untere Rand der Kleibodenschicht ist gegeben durch $g(x)=f(x)-1{,}5$ .
Berechne dann $\displaystyle\int_a^{b}\left(f(x)-g(x)\right)\;dx.$
An der Stelle $x=42$ wird senkrecht zum oberen Rand des Querschnitts eine $1{,}30 m$ lange geradlinige Bohrung durchgeführt.
Untersuchen Sie, ob diese Bohrung den Sandkern erreicht. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normale
Aufstellen der Normalen
Punkt $P(42|f(42))\;\Rightarrow\;P\left(42|\frac{64701}{12500}\right)$
Die Ableitung an der Stelle $x=42$ ist: $f'(42)=-\dfrac{24051}{25000}$
Die Normalengleichung lautet: $n(x)=-\dfrac{1}{f'(x_0)}(x-x_0)+f(x_0)$
Mit den angegebenen Werten erhält man:
$n(x)\approx1{,}0395\cdot x-38{,}4811$
Schnittpunkt der Normalen $n(x)$ mit $g(x)$
Mit $x_N\approx41{,}23$ erhält man $g(41{,}23)\approx4{,}371$ .
Dann gilt für die Länge der Strecke in der Kleibodenschicht:
Diese Länge ist kleiner als $1{,}3$ , d.h der Sandkern wird erreicht.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $P(42|f(42))$ und $f'(42)$ und ermittle die Normalengleichung: $n(x)=-\dfrac{1}{f'(x_0)}(x-x_0)+f(x_0)$
Berechne den Schnittpunkt der Normalen $n(x)$ mit der Gleichung für den oberen Randverlauf des Sandkerns $g(x)$ $\;\Rightarrow\;x_N$
Für die Länge der Strecke in der Kleibodenschicht gilt: $d=\sqrt{(42-x_N)^2+(f(42)-g(x_N))^2}$
Vergleiche $d$ mit der Länge der geradlinigen Bohrung.
Der obere Rand des Querschnitts des Sandkerns wird neu modelliert.
Der obere Rand des Querschnitts des Klimadeiches wird weiterhin durch $f$ beschrieben.
Gegeben ist die auf $\mathbb{R}$ definierte Funktionenschar $g_{k}$ mit
$g_{k}(x)=0{,}3 \cdot(x-k)^{2} \cdot e^{0{,}16 \cdot(x-k)+0{,}2}$ .
Die Graphen von $g_{k}$ sollen für $5 \leq x \leq 42$ und $41{,}5 \leq k \leq 47{,}5$ den oberen Rand des
Querschnitts des Sandkerns beschreiben.
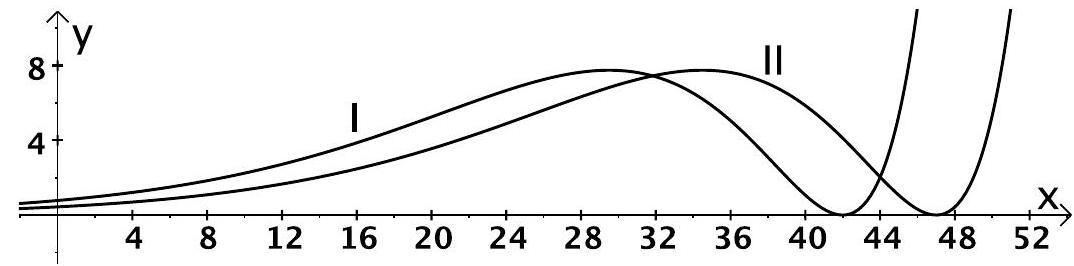
In der Abbildung sind die Graphen von zwei Vertretern von $g_{k}$ abgebildet.
Geben Sie für Graph I
und Graph II jeweils
einen Näherungswert
für $k$ an.
Begründen Sie Ihre Angaben. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Berührpunkte bei Funktionsgraphen
Näherungswert für $k$ für Graph I und Graph II
Der Graph von $g_{k}(x)=0{,}3 \cdot(x-k)^{2} \cdot e^{0{,}16 \cdot(x-k)+0{,}2}$ besitzt an der Stelle $x=k$ eine doppelte Nullstelle. Doppelte Nullstellen bedeuten, dass der Graph von $g_k$ einen Berührpunkt mit der x-Achse hat.
Hier hat der Graph I an der Stelle $x\approx 42$ einen Berührpunkt mit der x-Achse $\Rightarrow\; k\approx42$
Der Graph II hat an der Stelle $x\approx 47$ einen Berührpunkt mit der x-Achse $\Rightarrow\; k\approx47$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Graph von $g_{k}(x)=0{,}3 \cdot(x-k)^{2} \cdot e^{0{,}16 \cdot(x-k)+0{,}2}$ besitzt an der Stelle $x=k$ eine doppelte Nullstelle.
Doppelte Nullstellen bedeuten, dass der Graph von $g_k$ einen Berührpunkt mit der x-Achse hat.
Finde in der Abbildung jeweils die Berührstellen mit der x-Achse.

Die vertikale Dicke der Abdeckungsschicht aus Kleiboden soll

$2 m$ an der Stelle $x=14$ betragen und
im Querschnitt im Bereich $5 \leq x \leq 42$ an jeder Stelle mindestens $0{,}95 \mathrm{~m}$ betragen.

Untersuchen Sie, ob es einen Wert für $k$ mit $41{,}5 \leq k \leq 47{,}5$ gibt, sodass beide Bedingungen gleichzeitig erfüllt sind. (7 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert

Gibt es einen Wert für $k$ mit $41{,}5 \leq k \leq 47{,}5$ , sodass beide Bedingungen gleichzeitig erfüllt sind?

Bedingung I:

Man erhält die Gleichung $f(14)-g_k(14)=2$ .

Im Bereich $41{,}5 \leq k \leq 47{,}5$ liegt die Lösung der Gleichung $f(14)-g_k(14)=2$ bei $k\approx 46{,}9$ .

Bedingung II:

Die vertikale Dicke soll im Querschnitt im Bereich $5 \leq x \leq 42$ an jeder Stelle mindestens $0{,}95 \mathrm{~m}$ betragen.

Man erhält für $5 \leq x \leq 42$ die Gleichung $f(x)-g_{46{,}9}(x)\geq 0{,}95$ .

Berechne für $x$ aus dem gegebenen Intervall einige Werte $f(x)-g_{46{,}9}(x)$ und vergleiche.

x	$f(x)-g_{46{,}9}(x)$	Vergleich
$20$	$2{,}22$	$>0{,}95$
$30$	$1{,}54$	$>0{,}95$
$35$	$0{,}98$	$>0{,}95$
$38$	$0{,}90$	$<0{,}95$

Die letzte Tabellenzeile führt zu einem Widerspruch der Behauptung.

Es gibt keinen Wert für $k$ , der beide Bedingungen erfüllt.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

4

Aufgabe 2A

Für ein Land wird die Bevölkerungsgruppe der Erwachsenen betrachtet. In dieser

Bevölkerungsgruppe beträgt der Anteil der Internetnutzer $88 \%$ ; der Anteil derjenigen, die mindestens 65 Jahre alt sind und das Internet nutzen, beträgt $17 \%$ . Die betrachtete Bevölkerungsgruppe besteht aus 60,7 Millionen Personen, von denen 16,4 Millionen mindestens 65 Jahre alt sind.

Aus der betrachteten Bevölkerungsgruppe wird eine Person zufällig ausgewählt. Untersucht werden folgende Ereignisse:

A: „Die Person nutzt das Internet.“

B: „Die Person ist mindestens 65 Jahre alt.“

Stellen Sie den Sachzusammenhang in einer vollständig ausgefüllten Vierfeldertafel dar.
(3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
Vierfeldertafel
A: „Die Person nutzt das Internet.“
B: „Die Person ist mindestens 65 Jahre alt.“
Dann ist gegeben:
$P(A)=88\;\%$ und $P(A\cap B)=17\;\%$
$\Rightarrow\;P(\overline{B}\cap A)=88\;\%-17\;\%=71\;\%$
Weiterhin ist $P(B)=\dfrac{16{,}4\cdot 10^6}{60{,}7\cdot 10^6}\approx27\;\%$ .
Dann ist $P(\overline{B})=1-P(B)=73\;\%$ .
$P(\overline{A}\cap B)=P(B)-P(A\cap B)=27\;\%-17\;\%=10\;\%$
$P(\overline{A}\cap \overline{B})=P(\overline{B})-P(A\cap \overline{B})=73\;\%-71\;\%=2\;\%$
$P(\overline{A})=P(\overline{A}\cap B)+P(\overline{A}\cap \overline{B})=10\;\%+2\;\%=12\;\%$
Das ergibt folgende Vierfeldertafel:
Ausgefüllte Vierfeldertafel
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es ist gegeben: $P(A)=88\;\%$ und $P(A\cap B)=17\;\%$
Ergänze die Vierfeldertafel.
Untersuchen Sie, ob die Ereignisse $A$ und $B$ stochastisch unabhängig sind. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Unabhängigkeit von Ereignissen
Sind die Ereignisse $A$ und $B$ stochastisch unabhängig?
Es gilt zum Beispiel: $P_B(A)=\dfrac{P(A\cap B)}{P(B)}=\dfrac{17\;\%}{27\;\%}\approx63\;\%$
Andererseits ist aber $P(A)=88\;\%$ .
Da $P_B(A)\neq P(A)\;\Rightarrow\;A$ und $B$ sind stochastisch abhängig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne zum Beispiel $P_B(A)=\dfrac{P(A\cap B)}{P(B)}$ und vergleiche mit $P(A)$ .
Beschreiben Sie das Ereignis „ $\bar{A}$ und $B^{\prime \prime}$ im Sachzusammenhang. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ereignisse
Ereignis „⁣ $\bar{A}$ und $B$ " im Sachzusammenhang
$\overline{A}$ : „Die Person nutzt kein Internet.“
$B$ : „Die Person ist mindestens 65 Jahre alt.“
Dann ist „⁣ $\overline{A}$ und $B$ ": Die Person ist mindestens 65 Jahre alt und nutzt das Internet nicht.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$\overline{A}$ : „Die Person nutzt kein Internet.“
$B$ : „Die Person ist mindestens 65 Jahre alt.“
Beschreibe damit das Ereignis „ $\bar{A}$ und $B^{\prime \prime}$ .
Bestimmen Sie für den Fall, dass die ausgewählte Person jünger als 65 Jahre ist, die Wahrscheinlichkeit dafür, dass sie das Internet nutzt. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
Ausgewählte Person ist jünger als 65 Jahre und nutzt das Internet
A: „Die Person nutzt das Internet.“
$\overline{B}$ : „Die Person ist jünger als 65 Jahre.“
$P(A\cap \overline{B})=71\;\%$ und $P(\overline{B})=73\;\%$ (siehe Vierfeldertafel)
Dann ist $P_{\overline{B}}(A)=\dfrac{P(A\cap \overline{B})}{P(\overline{B})}=\dfrac{71\;\%}{73\;\%}\approx97\;\%$
Die gesuchte Wahrscheinlichkeit beträgt rund $97\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es ist $A$ : „Die Person nutzt das Internet.“ und $\overline{B}$ : „Die Person ist jünger als 65 Jahre.“
Gesucht ist die bedingte Wahrscheinlichkeit $P_{\overline{B}}(A)$ .
In der betrachteten Bevölkerungsgruppe nutzen etwa $72 \%$ das Internet mit einem Smartphone.
Aus der betrachteten Bevölkerungsgruppe werden 150 Personen zufällig ausgewählt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Anzahl derjenigen ausgewählten Personen, die das Internet mit einem Smartphone nutzen, weniger als $10 \%$ vom Erwartungswert dieser Anzahl abweicht. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
Wahrscheinlichkeit, dass die Anzahl derjenigen ausgewählten Personen, die das Internet mit einem Smartphone nutzen, weniger als $10 \%$ vom Erwartungswert dieser Anzahl abweicht
Es ist $X$ : die Anzahl derjenigen, die das Internet mit einem Smartphone nutzen
Dabei ist $X$ binomialverteilt mit $p= 0{,}72$ und $n= 150$ .
Der Erwartungswert beträgt: $\mu=n\cdot p=150\cdot 0{,}72=108$
$10\;\%$ vom Erwartungswert: $0{,}1\cdot 108=10{,}8$
Dann ist $\mu-10\;\%$ von $\mu=108-10{,}8=97{,}2$ und $\mu+10\;\%$ von $\mu=108+10{,}8=118{,}8$
Das genaue Intervall um den Erwartungswert ist $[97{,}2;118{,}8]$ . Da es nur ganze Personen gibt, müssen die Werte auf jeden Fall gerundet werden. Das Intervall wird kleiner gerundet $[98;118],$ da die Werte $97$ bzw. $119$ um mehr als $10\;\%$ vom Erwartungswert entfernt sind. Die Vorgabe laut Aufgabenstellung ist "weniger als $10 \%$ ".
Also wird berechnet: $P(98\leq X\leq 118)=\text{binomCdf}(150{,}0.72{,}0,118)-\text{binomCdf}(150{,}0.72{,}0,97)$
$P(98\leq X\leq 118)\approx0{,}9745-0{,}0301\approx0{,}9444$
Die Wahrscheinlichkeit, dass die Anzahl derjenigen ausgewählten Personen, die das Internet mit einem Smartphone nutzen, weniger als $10 \%$ vom Erwartungswert dieser Anzahl abweicht, beträgt rund $94\;\%.$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es ist $X$ : die Anzahl derjenigen, die das Internet mit einem Smartphone nutzen. $X$ ist binomialverteilt mit $p= 0{,}72$ und $n= 150$ .
Berechne $\mu\pm (10\;\%$ von $\mu$ ) und runde die Intervallgrenzen entsprechend $\;\Rightarrow\;[X_1;X_2]$
Berechne $P(X_1\leq X\leq X_2)$ .
Ermitteln Sie, wie viele Personen aus der betrachteten Bevölkerungsgruppe mindestens zufällig ausgewählt werden müssen, damit mit einer Wahrscheinlichkeit von mehr als $98 \%$ mehr als zwei dieser Personen das Internet mit einem Smartphone nutzen. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Anzahl der Personen bestimmen
Es ist $P(X>2)=1-P(X\leq 2)>0{,}98\;\Rightarrow\;P(X\leq 2)<0{,}02$
Berechnung mit dem GeoGebra TR
Damit ist $n\geq 8$ .
Es müssen mindestens $8$ Personen ausgewählt werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Löse die Ungleichung $P(X>2)>0{,}98$ .
In zwei Behältern befinden sich insgesamt 300 Kugeln, von denen 105 weiß und die übrigen schwarz sind. Im ersten Behälter befinden sich $k$ Kugeln, von denen $w$ weiß sind.
Jedem Behälter wird eine Kugel zufällig entnommen.
Interpretieren Sie den Term $\frac{195-(k-w)}{300-k}$ im Sachzusammenhang. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Term $\frac{195-(k-w)}{300-k}$ im Sachzusammenhang
Wenn sich im 1. Behälter $k$ Kugeln befinden, dann sind im 2. Behälter $300-k$ Kugeln.
Im 1. Behälter sind $w$ Kugeln weiß. Dann sind im 2. Behälter $105-w$ Kugel weiß.
Die Wahrscheinlichkeit aus dem 2. Behälter eine weiße Kugel zu ziehen ist:
Die Wahrscheinlichkeit aus dem 2. Behälter eine schwarze Kugel zu ziehen ist:
Der Term $\dfrac{195-(k-w)}{300-k}$ ist demnach die Wahrscheinlichkeit aus dem 2. Behälter eine schwarze Kugel zu ziehen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Wenn sich im 1. Behälter $k$ Kugeln befinden, dann sind im 2. Behälter $300-k$ Kugeln. Der gegebene Term bezieht sich also auf den 2. Behälter.
Überlege, wie groß die Wahrscheinlichkeit ist, aus diesem Behälter eine weiße bzw. schwarze Kugel zu ziehen und vergleiche mit dem gegebenen Term.

Es gilt:

I. Mit einer Wahrscheinlichkeit von $12{,}5 \%$ sind beide entnommenen Kugeln weiß.

II. Mit einer Wahrscheinlichkeit von $37{,}5 \%$ ist die aus dem ersten Behälter entnommene Kugel schwarz und die aus dem zweiten Behälter entnommene Kugel weiß.

Ermitteln Sie die Anzahl der weißen Kugeln im ersten Behälter. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln

Anzahl der weißen Kugeln im ersten Behälter

I. Mit einer Wahrscheinlichkeit von $12{,}5\; \%$ sind beide entnommenen Kugeln weiß.

Die Wahrscheinlichkeit eine weiße Kugel aus dem 1. Behälter zu ziehen ist $P(w)=\dfrac{w}{k}$ und ebenfalls eine weiße Kugel aus dem 2. Behälter zu ziehen ist $P(w)=\dfrac{105-w}{300-k}$ .

Dann gilt:

$P(ww)=\dfrac{w}{k} \cdot\dfrac{105-w}{300-k}=0{,}125$

II. Mit einer Wahrscheinlichkeit von $37{,}5 \;\%$ ist die aus dem ersten Behälter entnommene Kugel schwarz und die aus dem zweiten Behälter entnommene Kugel weiß.

Die Wahrscheinlichkeit eine schwarze Kugel aus dem 1. Behälter zu ziehen ist $P(s)=\dfrac{k-w}{k}$ und eine weiße Kugel aus dem 2. Behälter zu ziehen ist $P(w)=\dfrac{105-w}{300-k}$ .

Dann gilt:

$P(sw)=\dfrac{k-w}{k} \cdot\dfrac{105-w}{300-k}=0{,}375$

Es gibt nun ein lineares Gleichungssystem für die Unbekannten $k$ und $w$ :

$\mathrm{(I)}: \dfrac{w}{k} \cdot\dfrac{105-w}{300-k}=0{,}125$

$\mathrm{(II)}: \dfrac{k-w}{k} \cdot\dfrac{105-w}{300-k}=0{,}375$

Da beide Gleichungen den Term $\dfrac{105-w}{300-k}$ als Faktor enthalten, kann

Gleichung $\mathrm{(II)}$ durch Gleichung $\mathrm{(I)}$ geteilt werden.

$\Rightarrow\;\dfrac{\dfrac{k-w}{k}}{\dfrac{w}{k}}=\dfrac{0{,}375}{0{,}125}=3\;\Rightarrow\;\dfrac{k-w}{w}=3\;\Rightarrow\;\dfrac{k}{w}-1=3$

$\Rightarrow\;\dfrac{k}{w}=4$ bzw. $k=4w$

Setze $k=4w$ in Gleichung $\mathrm{(I)}$ ein:

$\displaystyle \dfrac{w}{k} \cdot\dfrac{105-w}{300-k}$	$=$	$\displaystyle 0{,}125$
	↓	Setze $k=4w$ ein.
$\displaystyle \dfrac{w}{4w} \cdot\dfrac{105-w}{300-4w}$	$=$	$\displaystyle 0{,}125$
	↓	Kürze im 1. Bruch mit $w.$
$\displaystyle \dfrac{1}{4} \cdot\dfrac{105-w}{300-4w}$	$=$	$\displaystyle 0{,}125$	$\displaystyle \cdot 4\cdot(300-4w)$
$\displaystyle 105-w$	$=$	$\displaystyle 0{,}125\cdot 4\cdot(300-4w)$
	↓	Vereinfache.
$\displaystyle 105-w$	$=$	$\displaystyle 150-2w$	$\displaystyle +2w-105$
$\displaystyle w$	$=$	$\displaystyle 45$

Die Anzahl der weißen Kugeln im ersten Behälter beträgt $45$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

5

Aufgabe 2B

Ein Unternehmen produziert Stahlkugeln für Kugellager. Erfahrungsgemäß sind $4 \%$ aller Kugeln fehlerhaft.

800 Kugeln werden zufällig ausgewählt. Die Anzahl der fehlerhaften Kugeln unter den ausgewählten kann durch eine binomialverteilte Zufallsgröße beschrieben werden.

Bestimmen Sie die Wahrscheinlichkeit dafür, dass unter den ausgewählten Kugeln weniger als 30 fehlerhaft sind. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Die Wahrscheinlichkeit, dass unter den ausgewählten Kugeln weniger als 30 fehlerhaft sind
$X$ : Anzahl der fehlerhaften Kugeln
Es ist $p=0{,}04$ und $n=800$ .
Dann gilt: $P(X<30)=\text{binomCdf}(800{,}0.04{,}0,29)\approx0{,}3341$
Die Wahrscheinlichkeit, dass unter den ausgewählten Kugeln weniger als $30$ fehlerhaft sind, beträgt rund $33{,}4\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $P(X<30)=P(X\leq29)$ .
Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Anzahl der fehlerhaften Kugeln unter den ausgewählten höchstens um eine halbe Standardabweichung vom Erwartungswert dieser Anzahl abweicht. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
Wahrscheinlichkeit, dass die Anzahl höchstens um eine halbe Standardabweichung vom Erwartungswert abweicht
Es gilt: $\mu=n\cdot p=800\cdot 0{,}04=32$
$\sigma=\sqrt{n\cdot p\cdot (1-p)}=\sqrt{800\cdot 0{,}04\cdot 0{,}96}\approx5{,}54$
$\dfrac{\sigma}{2}=2{,}8$
Dann ist $\mu-\dfrac{\sigma}{2}=29{,}2\color{blue}\approx 30$ und $\mu+\dfrac{\sigma}{2}=34{,}8\color{blue}\approx 34$
Mit diesen Werten erhält man:
$P(30\leq X\leq34)=\text{binomCdf}(800{,}0.04{,}0,34)-\text{binomCdf}(800{,}0.04{,}0,29)$
$P(30\leq X\leq34)\approx0{,}348$
Die Wahrscheinlichkeit, dass die Anzahl der fehlerhaften Kugeln unter den ausgewählten höchstens um eine halbe Standardabweichung vom Erwartungswert dieser Anzahl abweicht, beträgt rund $34{,}8\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $\mu$ und $\sigma$ .
Berechne die Intervallgrenzen $\mu \pm \dfrac{\sigma}{2}$ und runde die Werte entsprechend.
Berechne mit den gerundeten Werten $P\left(\mu - \dfrac{\sigma}{2}\leq X\leq \mu + \dfrac{\sigma}{2}\right)$
Eine Stahlkugel hat entweder keinen Fehler, einen Formfehler oder einen Größenfehler. Die Wahrscheinlichkeit für einen Formfehler beträgt $3 \%$ , die für einen Größenfehler $1 \%$ .
Alle Kugeln werden vor dem Verpacken geprüft. Dabei werden $95 \%$ der Kugeln mit Formfehler, $98 \%$ der Kugeln mit Größenfehler, aber auch $0{,}5\%$ der Kugeln ohne Fehler aussortiert.
Stellen Sie den Sachzusammenhang in einem beschrifteten Baumdiagramm dar.
(4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Beschriftetes Baumdiagramm
$A$ : Die Stahlkugeln werden aussortiert
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Erstelle mit den Angaben ein Baumdiagramm.
Geben Sie das Ergebnis des folgenden Terms an und interpretieren Sie die Bedeutung des Ergebnisses im Sachzusammenhang: (3 BE)
$0{,}96 \cdot 0{,}005 \cdot 800$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Ergebnis des Terms
$0{,}96 \cdot 0{,}005 \cdot 800=3{,}84$
Der Term hat den Wert $3{,}84$ .
Bedeutung des Ergebnisses im Sachzusammenhang
$0{,}96 \cdot 0{,}005$ ist die Multiplikation der Pfadwahrscheinlichkeiten des ersten Pfades. Das ist die Wahrscheinlichkeit, dass die Stahlkugel keinen Fehler hat und trotzdem aussortiert wird.
Diese Wahrscheinlichkeit multipliziert mit $800$ ergibt die zu erwartende Anzahl ( $3{,}84$ ) unter den 800 Kugeln an, die keinen Fehler haben und trotzdem aussortiert werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Berechne den gegebenen Term.
Teil 2
Betrachte den ersten Pfad des Baumdiagramms.

Berechnen Sie die Wahrscheinlichkeit dafür, dass eine aussortierte Kugel keinen Formfehler hat. (3 BE)

Bei Stahlkugeln, die während der ersten Überprüfung nicht aussortiert wurden, wird die Überprüfung aus Sicherheitsgründen ein weiteres Mal durchgeführt.
Berechnen Sie die Wahrscheinlichkeit dafür, dass eine bei der zweiten Überprüfung aussortierte Kugel keinen Fehler aufweist. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Wahrscheinlichkeit, dass eine bei der zweiten Überprüfung aussortierte Kugel keinen Fehler aufweist
Das Baumdiagramm wird bei nicht aussortierten Kugeln um eine Stufe erweitert.
Dann ergeben sich für die Fälle der Aussortierung bei der 2. Prüfung folgende Anteile:
Die Stahlkugel hat keinen Fehler: $0{,}96\cdot 0{,}995\cdot 0{,}005=0{,}004776$
Die Stahlkugel hat einen Formfehler: $0{,}03\cdot 0{,}95\cdot 0{,}05=0{,}001425$
Die Stahlkugel hat einen Größenfehler: $0{,}01\cdot 0{,}02\cdot 0{,}98=0{,}000196$
Die Summe dieser drei Anteile beträgt $0{,}006397$ .
Für die gesuchte Wahrscheinlichkeit gilt dann:
Die Wahrscheinlichkeit, dass eine bei der zweiten Überprüfung aussortierte Kugel keinen Fehler aufweist, beträgt rund $74{,}7\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Das Baumdiagramm wird bei nicht aussortierten Kugeln um eine Stufe erweitert.
Berechne für die Fälle der Aussortierung bei der 2. Prüfung die drei entsprechenden Anteile.
Die gesuchte Wahrscheinlichkeit ist dann der Quotient aus dem Anteil "Stahlkugel hat keinen Fehler" und der Summe dieser drei Anteile.
Die Kugeln werden in Packungen verkauft. Ein Teil der verkauften Packungen wird zurückgegeben. Die Wahrscheinlichkeit dafür, dass eine verkaufte Packung zurückgegeben wird, beträgt $3\;\%$ . Dem Unternehmen entsteht pro Packung, die zurückgegeben wird, ein Verlust von 5,80 Euro. Pro Packung, die nicht zurückgegeben wird, erzielt das Unternehmen einen Gewinn von 8,30 Euro.
Bestimmen Sie die Wahrscheinlichkeit, mit der das Unternehmen bei einem Verkauf von 200 Packungen einen Gesamtgewinn von mindestens 1500 Euro erzielt. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Wahrscheinlichkeit, mit der das Unternehmen bei einem Verkauf von 200 Packungen einen Gesamtgewinn von mindestens 1500 Euro erzielt
Zufallsgröße $Y$ : sie beschreibt die Anzahl $y$ der zurückgegebenen Packungen
$Y$ ist binomialverteilt mit $n= 200$ und $p= 0{,}03$ .
$200-y$ ist die Anzahl der Packungen, die einen Gewinn von $8{,}30\;€$ erbringen, d.h. $(200-y)\cdot 8{,}30$ ist der erzielte Gewinn.
Die Anzahl $y$ der zurückgegebenen Packungen ergeben einen Verlust von $y\cdot 5{,}80\;€$ .
Der Gesamtgewinn von mindestens $1500$ Euro soll erzielt werden:
Gewinn $-$ Verlust $\geq 1500$ $\;\Rightarrow\;(200-y)\cdot 8{,}30 -y\cdot 5{,}80\geq 1500$
Der GTR liefert für die Gleichung $(200-y)\cdot 8{,}30 -y\cdot 5{,}80= 1500$ die Lösung $y\approx11{,}3475...$
Dann ist $y\leq 11$ , da es nur ganze Packungen gibt. (Für $y\leq11$ ist die linke Seite der Gleichung größer als $1500$ .)
Für $y\leq 11$ folgt dann:
Die Wahrscheinlichkeit, mit der das Unternehmen bei einem Verkauf von $200$ Packungen einen Gesamtgewinn von mindestens $1500$ Euro erzielt, beträgt rund $98{,}2\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$200-y$ ist die Anzahl der Packungen, die einen Gewinn von $8{,}30\;€$ erbringen.
Die Anzahl $y$ der zurückgegebenen Packungen ergeben einen Verlust von $y\cdot 5{,}80\;€$ .
Gewinn $-$ Verlust $\geq 1500\;\Rightarrow\;$ Wert für y
Berechne die kumulierte Wahrscheinlichkeit für diesen gefundenen Wert.

6

Aufgabe 2C

Der Wasserverbrauch bei einem Waschgang wird für eine Waschmaschine als normalverteilt mit dem Erwartungswert 45 Liter und der Standardabweichung 1,2 Liter angenommen.

Ermitteln Sie die Wahrscheinlichkeit dafür, dass diese Maschine bei einem Waschgang
- mehr als 45 Liter verbraucht.
- weniger als 47 Liter verbraucht.
- auf ganze Liter gerundet 45 Liter verbraucht.
(5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Bei einem Waschgang werden mehr als 45 Liter verbraucht
$X$ ist der Wasserverbrauch für einen Waschgang in Litern.
$P(X>45)=\text{normCdf}(45,\infty,45, 1.2)=0{,}5$
Die Wahrscheinlichkeit, dass bei einem Waschgang mehr als 45 Liter verbraucht werden, beträgt $50\;\%$ .
Bei einem Waschgang werden weniger als 47 Liter verbraucht
$P(x<47)=\text{normCdf}(-\infty,47{,}45, 1.2)\approx0{,}9522$
Die Wahrscheinlichkeit, dass bei einem Waschgang weniger als 47 Liter verbraucht werden, beträgt rund $95\;\%$ .
Bei einem Waschgang werden auf ganze Liter gerundet 45 Liter verbraucht
$P(44{,}5\leq X<45{,}5)=\text{normCdf}(44.5{,}45.5{,}45{,}1.2)\approx0{,}3231$
Die Wahrscheinlichkeit, dass bei einem Waschgang auf ganze Liter gerundet $45$ Liter verbraucht werden, beträgt rund $32\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die Wahrscheinlichkeit der Ereignisse kann mithilfe der Verteilungsfunktion berechnet werden:
Mehr als 45 Liter verbraucht: $P(X>45)=\text{normCdf}(.............)$
Weniger als 47 Liter verbraucht: $P(x<47)=\text{normCdf}(.............)$
Auf ganze Liter gerundet 45 Liter verbraucht: $P(44{,}5\leq X<45{,}5)=\text{normCdf}(.............)$
Berechnen Sie ein symmetrisches Intervall um den Erwartungswert, sodass der Wasserverbrauch bei einem Waschgang mit einer Wahrscheinlichkeit von $5\,\%$ außerhalb dieses Intervalls liegt. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Symmetrisches Intervall
Es soll gelten: $P(X\leq 45-r)=2{,}5\;\%$
Diese Gleichung hat die Lösung $r\approx2{,}35$ .
Das gesuchte Intervall ist dann $[45 − r; 45 + r]=[42{,}65;47{,}35]$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Löse die Gleichung $P(X\leq 45-r)=2{,}5\;\%$ für die Unbekannte $r$ .
Bei einer anderen Maschine ist der Wasserverbrauch näherungsweise normalverteilt mit dem Erwartungswert 60 Liter, aber unbekannter Standardabweichung. Bei $10 \%$ der Waschgänge werden bei dieser Maschine mehr als 65 Liter verbraucht.
Bestimmen Sie die unbekannte Standardabweichung. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Bestimmen der Standardabweichung
$Y$ : Wasserverbrauch für einen Waschgang in Litern
$\mu=60,$ $\sigma$ unbekannt
Es soll gelten: $P(Y>65)=0{,}1$ mit unbekanntem $\sigma$
Diese Gleichung hat die Lösung $\sigma\approx3{,}9015$ .
Die Standardabweichung beträgt rund $3{,}9$ Liter.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Löse die Gleichung $P(Y>65)=0{,}1$ mit unbekannter Standardabweichung $\sigma$ .
Bei einer Massenproduktion von Steuerelementen für Waschmaschinen haben $12 \%$ der Steuerelemente einen Defekt. Vor dem Einbau werden die Steuerelemente geprüft.
Ein älteres Prüfgerät erkennt ein defektes Steuerelement mit einer Wahrscheinlichkeit von $90 \%$ . Dieses Prüfgerät zeigt allerdings auch einwandfreie Steuerelemente fälschlicherweise mit einer Wahrscheinlichkeit von $5 \%$ als defekt an.
Weisen Sie nach, dass die Wahrscheinlichkeit, mit der das Prüfgerät eine richtige Entscheidung trifft, etwa $94 \%$ beträgt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass trotz Prüfung ein defektes
Steuerelement eingebaut wird. (6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Wahrscheinlichkeit bestimmen
Das Prüfgerät trifft eine richtige Entscheidung, wenn es ein defektes Bauteil als defekt oder ein funktionierendes Bauteil als nicht defekt erkennt.
$P(\text{richtige Entscheidung}) = 0{,}12 \cdot 0{,}9 + 0{,}88 \cdot (1-0{,}05) =0{,}944$
Damit ist gezeigt, dass die Wahrscheinlichkeit, mit der das Prüfgerät eine richtige Entscheidung trifft, etwa $94 \;\%$ beträgt.
Die Wahrscheinlichkeit dafür, dass trotz Prüfung ein defektes Steuerelement eingebaut wird
Hier hilft ein Baumdiagramm:
$D$ : Steuerelement hat einen Defekt
$\overline {D}$ : Steuerelement hat keinen Defekt
$E$ : defektes Steuerelement wird erkannt
$\overline {E}$ : defektes Steuerelement wird nicht erkannt
Es ist:
$P(\overline {E})=P(D\cap \overline {E})+P(\overline {D}\cap \overline {E})=0{,}12\cdot 0{,}1+0{,}88\cdot 0{,}95=0{,}848$
Weiterhin ist:
$P_{ \overline {E}}(D)=\dfrac{P(D\cap \overline {E})}{P( \overline {E})}=\dfrac{0{,}12\cdot 0{,}1}{0{,}848}\approx0{,}01415$
Die Wahrscheinlichkeit dafür, dass trotz Prüfung ein defektes Steuerelement eingebaut wird, beträgt rund $1{,}4\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Das Prüfgerät trifft eine richtige Entscheidung, wenn es ein defektes Bauteil als defekt oder ein funktionierendes Bauteil als nicht defekt erkennt.
Wende die Pfadregeln an.
Teil 2
Berechne $P(\overline {E})$ und $P_{ \overline {E}}=\dfrac{P(D\cap \overline {E})}{P( \overline {E})}$ .
Ein neueres Prüfgerät trifft immer richtige Entscheidungen. Um die Anzahl von Prüfungen zu reduzieren, schaltet man zehn Steuerelemente hintereinander und prüft sie gleichzeitig. Ist mindestens eines der Steuerelemente defekt, so zeigt das Prüfgerät einen Defekt an. In diesem Fall wird zusätzlich jedes Steuerelement einzeln geprüft.
Interpretieren Sie den folgenden Term im Sachzusammenhang:
$0{,}88^{10} \cdot 1+\left(1-0{,}88^{10}\right) \cdot 11$
Untersuchen Sie, wie viele Steuerelemente jeweils hintereinandergeschaltet werden müssen, damit die zu erwartende Anzahl der Prüfungen im Verhältnis zur Anzahl von Einzelprüfungen am kleinsten ist. (7 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
Interpretieren im Sachzusammenhang
Gegeben ist der Term $0{,}88^{10} \cdot 1+\left(1-0{,}88^{10}\right) \cdot 11$ .
Anders dargestellt sieht der Term folgendermaßen aus:
Dabei ist $1-0{,}12=0{,}88$ die Wahrscheinlichkeit, dass die Steuerelemente keinen Defekt haben.
$0{,}88^{10}$ besagt, dass 10-mal hintereinander kein Defekt auftritt und $1$ ist die Anzahl der Überprüfungen.
Die Wahrscheinlichkeit für das Gegenereignis ist $1-0{,}88^{10}$ . Hierin sind alle Ereignisse vereinigt, bei denen mindestens ein Steuerteil defekt ist.
Die Zahl $11$ setzt sich zusammen aus $1+10$ , d.h. in der laufenden Prüfung (entspricht der $1$ ) wird mindestens ein defektes Steuerelement gefunden, sodass zusätzlich jedes Steuerelement einzeln geprüft wird (entspricht der $10$ ).
Somit gibt der Term die zu erwartende Anzahl (der Erwartungswert ist etwa $8{,}2$ ) benötigter Prüfungen für $10$ hintereinandergeschaltete Steuerelemente an.
Die zu erwartende Anzahl der Prüfungen im Verhältnis zur Anzahl von Einzelprüfungen soll am kleinsten sein
$n$ : ist die Anzahl der hintereinandergeschalteten Steuerelemente
Der Erwartungswert für die Anzahl der Prüfungen (analog zum 1. Teil) ist:
$E=0{,}88^n \cdot 1 + (1 − 0{,}88^n) \cdot (n + 1)$ mit $n\in \mathbb{N}$ und $n \geq 1$
Dann gilt für den Erwartungswert im Verhältnis zur Anzahl der Einzelprüfungen:
Bilde die Ableitung von $f(n)=\dfrac{0{,}88^n \cdot 1 + (1 − 0{,}88^n) \cdot (n + 1)}{n}$ und löse die Gleichung $f'(n)=0$ um das Minimum zu finden:
Die erste Lösung entfällt, da $n \geq 1$ sein muss.
Wegen $n\in \mathbb{N}$ ist die zweite Lösung $n=3$ oder $n=4$ .
$f(3)\approx 0{,}65186$ und $f(4)\approx 0{,}65030$ und $f(5)\approx0{,}67227$
Wie man sieht, ist der Wert von $f(4)$ am kleinsten.
Der Quotient ist für $n=4$ minimal.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Analysiere die einzelnen Terme in dem gegebenen Term. Der Term ist ein Erwartungswert (wofür?).
Teil 2
Bilde (analog zum Term im 1. Teil) den Erwartungswert $E$ für die Anzahl der Prüfungen in Abhängigkeit von $n$ .
Bilde den Quotienten aus $E$ und $n$ und bestimme das Minimum für diesen Quotienten.

7

Aufgabe 3A

Betrachtet werden die Pyramiden $A B C D S_{k}$

mit $A(0|0| 0), B(2|0| 0), C(2|2| 0), D(0|2| 0)$ und $S_{k}(1|1| k)$ mit $k>1$ .

Die gemeinsame Grundfläche $A B C D$ dieser Pyramiden ist quadratisch. Der Schnittpunkt der Diagonalen der Grundfläche $A B C D$ wird mit $T$ bezeichnet.

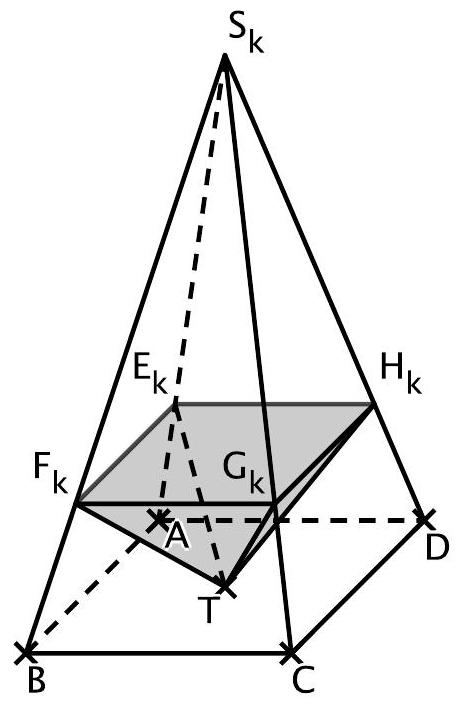
Die Abbildung zeigt beispielhaft eine dieser Pyramiden.

Berechnen Sie den Inhalt der Oberfläche der Pyramide $A B C D S_{k}$ . (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Inhalt der Oberfläche der Pyramide $A B C D S_{k}$
$O_{\text{Pyramide}}=G+4\cdot A_{\triangle}$
Dabei ist $G=2^2=4$ und $A_{\triangle}=\dfrac{1}{2}\cdot g \cdot h$
Die Grundseite des Dreiecks ist $g=2.$
Die Mitte der Seite $\overline{BC}$ ist der Punkt $M$ .
$\Rightarrow\;\vec m=\dfrac{1}{2}\cdot\left(\begin{pmatrix}2\\0\\0\end{pmatrix}+\begin{pmatrix}2\\2\\0\end{pmatrix}\right)=\begin{pmatrix}2\\1\\0\end{pmatrix}\;\Rightarrow\;M(2|1|0)$
Der Vektor $\overrightarrow{MS_k}=\begin{pmatrix}1\\1\\k\end{pmatrix}-\begin{pmatrix}2\\1\\0\end{pmatrix}=\begin{pmatrix}-1\\0\\k\end{pmatrix}$
Die Dreieckshöhe ist $h=|\overrightarrow{MS_k}|=\sqrt{(-1)^2+k^2}=\sqrt{1+k^2}.$
Dann folgt für den Inhalt der Pyramidenoberfäche:
.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es ist $O_{\text{Pyramide}}=G+4\cdot A_{\triangle}$
Für die Dreiecksfläche benötigst Du die Dreieckshöhe, für die gilt, $h=|\overrightarrow{MS_k}|$ , mit dem Punkt $M$ als Mitte der Seite $\overline{BC}$ .

Der Punkt $S_{k}$ wird am Punkt $C$ gespiegelt. Geben Sie die Koordinaten des Spiegelpunktes zu $S_{k}$ an.

Berechnen Sie den Wert von $k$ so, dass $S_{k}$ zu seinem Spiegelpunkt den Abstand 6 hat.

(4 BE)

Die Seitenfläche $A B S_{k}$ liegt in der Ebene $L$ .
Bestimmen Sie eine Gleichung von $L$ in Koordinatenform. (3 BE)
[zur Kontrolle: $k \cdot y-z=0]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Überblick
Gleichung von $L$ in Koordinatenform
$\overrightarrow{AB}=\begin{pmatrix}2\\0\\0\end{pmatrix}$ und $\overrightarrow{AS_k}=\begin{pmatrix}1\\1\\k\end{pmatrix}$
Es soll gelten:
$\vec n\circ \overrightarrow{AB}=0$ und $\vec n\circ \overrightarrow{AS_k}=0$
1. Gleichung: $\begin{pmatrix}n_1\\n_2\\n_3\end{pmatrix}\circ \begin{pmatrix}2\\0\\0\end{pmatrix}=0\;\Rightarrow\;2\cdot n_1+0+0=0\;\Rightarrow\;n_1=0$
2. Gleichung: $\begin{pmatrix}n_1\\n_2\\n_3\end{pmatrix}\circ \begin{pmatrix}1\\1\\k\end{pmatrix}=0$
Mit $n_1=0$ erhält man die Gleichung: $n_2+k\cdot n_3=0$
Wähle z.B. $n_3=-1,$ dann folgt: $n_2-k=0\;\Rightarrow\;n_2=k$ .
Der Normalenvektor lautet demnach: $\vec n=\begin{pmatrix}0\\k\\-1\end{pmatrix}$
Da die Ebene $L$ den Koordinatenursprung $A(0|0|0)$ enthält, gilt für die Ebenengleichung: $L:\;k\cdot y-z=0$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es gilt: $\vec n\circ \overrightarrow{AB}=0$ und $\vec n\circ \overrightarrow{AS_k}=0$ . Berechne den Normalenvektor $\vec n.$
Beachte $L$ verläuft durch den Koordinatenursprung.

Bestimmen Sie denjenigen Wert von $k$ , für den die Seitenfläche $A B S_{k}$ gegenüber der Grundfläche $A B C D$ um einen Winkel der Größe $60^{\circ}$ geneigt ist. (3 BE)

Untersuchen Sie, ob es einen Wert für $k>1$ gibt, sodass das Dreieck $B S_{k} D$ rechtwinklig ist. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Das Dreieck $B S_{k} D$ soll rechtwinklig sein
Berechne die Vektoren $\overrightarrow{BS_k}$ und $\overrightarrow{DS_k}$ und setze dann ihr Skalarprodukt gleich null.
$\overrightarrow{BS_k}=\begin{pmatrix}1\\1\\k\end{pmatrix}-\begin{pmatrix}2\\0\\0\end{pmatrix}=\begin{pmatrix}-1\\1\\k\end{pmatrix}$
$\overrightarrow{DS_k}=\begin{pmatrix}1\\1\\k\end{pmatrix}-\begin{pmatrix}0\\2\\0\end{pmatrix}=\begin{pmatrix}1\\-1\\k\end{pmatrix}$
$\overrightarrow{BS_k}\circ\overrightarrow{DS_k}=0\;\Rightarrow\;\begin{pmatrix}-1\\1\\k\end{pmatrix}\circ \begin{pmatrix}1\\-1\\k\end{pmatrix}=0$
Man erhält die Gleichung:
Da $k>1$ ist, erhält man als Lösung der Gleichung $k^2=2$ nur den positiven Wert $k=\sqrt{2}$ .
Für $k=\sqrt{2}$ ist das Dreieck $B S_{k} D$ rechtwinklig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Vektoren $\overrightarrow{BS_k}$ und $\overrightarrow{DS_k}$ und setze dann ihr Skalarprodukt gleich null. Löse die Gleichung nach $k$ auf.
Die Ebene mit der Gleichung $z=1$ schneidet die vier vom Punkt $S_{k}$ ausgehenden Kanten der Pyramide $A B C D S_{k}$ in den Punkten $E_{k}, F_{k}, G_{k}$ und $H_{k}$ (vgl. Abbildung).
Bestimmen Sie die $x$ - und die $y$ -Koordinate von $F_{k}$ . (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden
Die $x$ - und die $y$ -Koordinate von $F_{k}$
Der Punkt $F$ hat wegen $z=1$ die Koordinaten $F(x|y|1)$ .
Die Gerade durch die Punkte $B$ und $S_k$ hat die Gleichung:
$g_{BS_k}:\vec x=\overrightarrow{OB}+ r\cdot \overrightarrow{BS_k}=\begin{pmatrix}2\\0\\0\end{pmatrix} +r\cdot \begin{pmatrix}-1\\1\\k\end{pmatrix}$
Der Punkt $F$ liegt auf dieser Geraden:
$\Rightarrow\;\begin{pmatrix}2\\0\\0\end{pmatrix} +r\cdot \begin{pmatrix}-1\\1\\k\end{pmatrix}=\begin{pmatrix}x\\y\\1\end{pmatrix}$
Aus Gleichung $\mathrm{(III)}$ folgt dann $r=\dfrac{1}{k}$ .
$r=\dfrac{1}{k}$ eingesetzt liefert die x- und y-Koordinaten: $x=2-\dfrac{1}{k}$ und $y=\dfrac{1}{k}$ .
Damit hat der Punkt $F$ die Koordinaten $F(2-\frac{1}{k}|\frac{1}{k}|1)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Punkt $F$ hat wegen $z=1$ die Koordinaten $F(x|y|1)$ .
Erstelle die Gleichung der Geraden durch die Punkte $B$ und $S_k$ .
Setze in die Geradengleichung die Koordinaten von $F$ ein.
Bestimmen Sie diejenigen Werte von $k$ , für die das Verhältnis des Volumens der Pyramide $E_{k} F_{k} G_{k} H_{k} T$ zum Volumen der Pyramide $A B C D S_{k} \quad\frac{1}{8}$ beträgt. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Strahlensatz (Vierstreckensatz)
Verhältnis des Volumens der Pyramide $E_{k} F_{k} G_{k} H_{k} T$ zum Volumen der Pyramide $A B C D S_{k}$
Das Pyramidenvolumen ist $V=\dfrac{1}{3}\cdot G \cdot h$ .
Die Dreiecke $ABS_k$ und $E_kF_kS_k$ sind ähnlich.
$S_k$ hat die z-Koordinate $z=k$ .
Ein Punkt im Viereck $E_kF_kG_kH_k$ hat die z-Koordinate $z=1$ .
Dann gilt mit dem Strahlensatz:
$\Rightarrow\;\dfrac{|\overline{E_kF_K}|}{|\overline{AB}|}=\dfrac{k-1}{k}$
Das Verhältnis der beiden Pyramidenvolumina soll $\dfrac{1}{8}$ betragen:
Nach Kürzen mit $\dfrac{1}{3}$ und Einsetzen von $\dfrac{|\overline{E_kF_K}|}{|\overline{AB}|}=\dfrac{k-1}{k}$ folgt:
Gelöst mit dem GeoGebra TR
Du hast die Lösungen $k_1=-\sqrt{5}+3\approx0{,}764$ , $k_2=2$ und $k_3=\sqrt{5}+3\approx5{,}24$ erhalten. Die Lösung $k_1$ entfällt, da $k>1$ sein muss.
Für $k=2$ oder $k=\sqrt{5}+3$ beträgt das Verhältnis der beiden Pyramidenvolumina $\dfrac{1}{8}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es soll gelten: $\dfrac{V_{E_{k} F_{k} G_{k} H_{k} T}}{V_{A B C D S_{k}}}=\dfrac{1}{8}$
Die Dreiecke $ABS_k$ und $E_kF_kS_k$ sind ähnlich.
$S_k$ hat die z-Koordinate $z=k$ und ein Punkt im Viereck $E_kF_kG_kH_k$ hat die z-Koordinate $z=1$ .
Wende den Strahlensatz auf die Seiten $\overline{E_kF_K}$ und $\overline{AB}$ an.
Das Volumenverhältnis liefert dann eine Gleichung für $k$ .

8

Aufgabe 3B

Das Rechteck $O A E K$ stellt ein Tennisspielfeld dar. Die Koordinaten für die folgenden Punkte lauten: $O(0|0| 0), A(27|0| 0), B(27|18| 0), C(27|39| 0), E(27|78| 0), F(27|39| 3{,}5)$ , $H(0|39| 3{,}5)$ und $M(13{,}5|39| 3)$ .

Alle Koordinaten haben die Längeneinheit Fuß (ft). Das Netz ist an Pfosten befestigt, die durch die Strecken $\overline{C F}$ und $\overline{G H}$ dargestellt sind. Es hat an den Enden eine Höhe von $3{,}5\; \mathrm{ft}$ und fällt geradlinig ab, bis es in der Mitte $M$ nur noch eine Höhe von $3\; \mathrm{ft}$ hat. Der Boden wird durch die $x y$ -Ebene dargestellt. Der Ball wird als punktförmig angenommen.

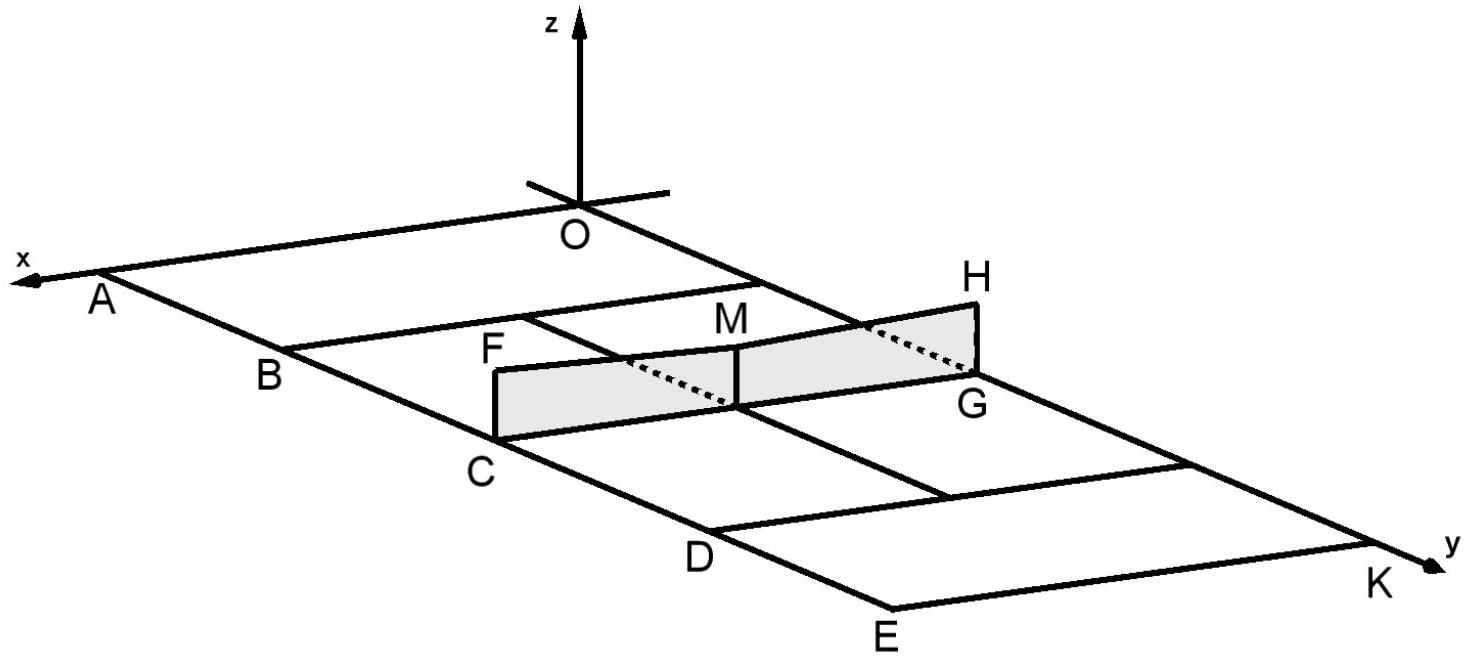
Geben Sie die Koordinaten des Punktes $D$ an.
Berechnen Sie die Länge der Diagonalen des Spielfeldes. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge eines Vektors
Koordinaten des Punktes $D$
$D$ hat dieselbe x-Koordinate wie der Punkt $A$ also $27$ .
Die y-Koordinate vom Punkt $B$ ist $18$ und die vom Punkt $C$ ist $39$ . Der Abstand der beiden Punkte $B$ und $C$ ist also $39-18=21$ .
Um die y-Koordinate des Punktes $D$ zu erhalten, muss zur y-Koordinate $39$ vom Punkt $C$ $21$ addiert werden $\;\Rightarrow\; 39+21=60$ .
Die z-Koordinate von $D$ ist $0\;\Rightarrow\;D(27|60|0)$
Berechnen Sie die Länge der Diagonalen des Spielfeldes
Die Länge der Diagonale ist:
Die Länge der Diagonalen des Spielfeldes beträgt rund $82{,}5\;\text{ft}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
$D$ hat dieselbe x-Koordinate wie der Punkt $A$ . Der Abstand der beiden Punkte $B$ und $C$ ist also $39-18=21$ . Addiere $21$ zur y-Koordinate von $C$ . $D$ liegt in der xy-Ebene.
Teil 2
Berechne den Betrag des Vektors $\overrightarrow{OE}$ .
Es kann vorausgesetzt werden, dass beim Aufschlag der Ball das Netz überquert und dass die $x$ -Koordinate zu diesem Zeitpunkt größer als $13{,}5$ ist. Die Flugbahn des Balls wird als geradlinig angenommen.
Bei einem Aufschlag wird der Ball im Punkt $P(13|0| 10{,}4)$ getroffen, fliegt in Richtung
$\def\arraystretch{1.25} \vec{v}=\left(\begin{array}{c}13 \\ 58{,}5 \\ -10{,}4\end{array}\right)$ und trifft im Punkt $Q$ auf dem Boden auf.
Zeigen Sie, dass $Q$ im Spielfeld liegt. (4 BE)
[zur Kontrolle: $Q(26|58{,}5| 0)$ ]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
Nachweis, dass $Q$ im Spielfeld liegt
Der Punkt $Q(x|y|0)$ liegt auf der Flugbahn $\vec x= \overrightarrow{OP}+r\cdot \vec v$ .
Aus Gleichung $\mathrm{(III)}$ folgt, dass $r=1$ ist.
Berechne mit $r=1$ die fehlenden Koordinaten von $Q$ :
$Q$ liegt im Spielfeld, da die x-Koordinate von $Q$ kleiner als $27$ (Spielfeldbreite) und die y-Koordinate von $Q$ kleiner als $78$ (Spielfeldlänge) ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Punkt $Q(x|y|0)$ liegt auf der Flugbahn.
Erstelle die Geradengleichung für die Flugbahn des Balles und setze sie gleich $Q$ . Löse das Gleichungssystem.
Betrachte die x- und y-Koordinaten von $Q$ und vergleiche sie mit der Spielfeldbreite und Spielfeldlänge.
Die Geschwindigkeit des Balles wird mit $90$ Fuß pro Sekunde als konstant angenommen.
Bestimmen Sie, wie viel Zeit vom Abschlag im Punkt $P$ bis zum Auftreffen des Balles auf dem Boden vergeht. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge eines Vektors
Zeit vom Abschlag im Punkt $P$ bis zum Auftreffen des Balles
Die Strecke in $\mathrm{ft}$ , die der Ball zurücklegt, ist $|\overrightarrow{PQ}|$ .
$|\overrightarrow{PQ}|=\sqrt{13^2+58{,}5^2+(-10{,}4)^2}=\sqrt{3699{,}41}\approx60{,}8\;\mathrm{ft}$
Der zurückgelegte Weg beträgt rund $60{,}8\;\mathrm{ft}$ .
Für die benötigte Zeit gilt:
Die Zeit vom Abschlag im Punkt $P$ bis zum Auftreffen des Balles auf dem Boden beträgt rund $0{,}68\;\mathrm{s}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Länge der Strecke $|\overrightarrow{PQ}|$ .
Berechne die Zeit im Flug mit dem Weg-Zeit-Gesetz: $t=\dfrac{s}{v}$

Berechnen Sie die Größe des Winkels, unter dem der Ball auf den Boden auftrifft.

(3 BE)

Spiegelt man die Gerade, die die Flugbahn des Balles beschreibt, an der $x y$ -Ebene, ergibt sich die Gerade $b$ . Die Gerade $b$ beschreibt die Flugbahn direkt nach dem Aufprall.
Bestimmen Sie eine Gleichung der Geraden $b$ . (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
Gleichung der Geraden $b$
Der Punkt $P(13|0|10{,}4)$ muss an der xy-Ebene gespiegelt werden.
$\Rightarrow\;P'(13|0|-10{,}4)$
Die Gerade $b$ geht durch die Punkte $P'(13|0|-10{,}4)$ und $Q(26|58{,}5| 0)$ .
$b:\;\vec x=\overrightarrow{OQ}+r\cdot \overrightarrow{P'Q}$
mit $r\in\mathbb{R}$ .
Die Gleichung der Geraden $b$ lautet: $\vec x=\begin{pmatrix}26\\58{,}5\\0\end{pmatrix}+r\cdot \begin{pmatrix}13\\58{,}5\\10{,}4\end{pmatrix}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Punkt $P(13|0|10{,}4)$ muss an der xy-Ebene gespiegelt werden $\;\Rightarrow\;P'$
Bestimme die Gerade $b$ durch die Punkte $P'$ und $Q$ .

Bei einem anderen Aufschlag wird der Ball im Punkt $P_{h}(13|0| h), h>0$ , abgeschlagen und trifft im Punkt $Q(26|58{,}5| 0)$ auf dem Boden auf. Der Ball überquert das Netz in einer Höhe von $0{,}25\; \mathrm{ft}$ über dem Netz.

Bestimmen Sie den zugehörigen Wert von $h$ . (8 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie

Wert von $h$

Die Gleichung für die Flugbahn des Balles lautet:

$k:\;\vec x=\overrightarrow{OP_h}+r\cdot \overrightarrow{P_hQ}$

$k:\;\vec x=\begin{pmatrix}13\\0\\h\end{pmatrix}+r\cdot \left(\begin{pmatrix}26\\58{,}5\\0\end{pmatrix}-\begin{pmatrix}13\\0\\h\end{pmatrix}\right)=\begin{pmatrix}13\\0\\h\end{pmatrix}+r\cdot \begin{pmatrix}13\\58{,}5\\-h\end{pmatrix}$ mit $r \in \mathbb{R}$

Der Ball überquert das Netz in einem Punkt $U(x|39|z_1)$ .

Der Punkt $U$ muss auf der Flugbahn $k$ liegen:

$\begin{pmatrix}x\\39\\z_1\end{pmatrix}=\begin{pmatrix}13\\0\\h\end{pmatrix}+r\cdot \begin{pmatrix}13\\58{,}5\\-h\end{pmatrix}\;\Rightarrow\; r=\dfrac{39}{58{,}5}=\dfrac{2}{3}$

Mit $r=\dfrac{2}{3}$ folgt für den Punkt $U$ :

$\vec x_U=\begin{pmatrix}13\\0\\h\end{pmatrix}+\frac{2}{3}\cdot \begin{pmatrix}13\\58{,}5\\-h\end{pmatrix}=\begin{pmatrix}\frac{65}{3}\\39\\\frac{1}{3}h\end{pmatrix}\;\Rightarrow\;U(\frac{65}{3}\mid 39\mid \frac{1}{3}h)$

Der Punkt $U$ liegt oberhalb der Netzkante $\overline{FM}$ . Deshalb wird die Netzoberkante durch folgende Gleichung beschrieben:

$l:\;\vec x=\overrightarrow{OF}+s\cdot \overrightarrow{FM}$

$l:\;\vec x=\begin{pmatrix}27\\39\\3{,}5\end{pmatrix}+s\cdot \left(\begin{pmatrix}13{,}5\\39\\3\end{pmatrix}-\begin{pmatrix}27\\39\\3{,}5\end{pmatrix}\right)=\begin{pmatrix}27\\39\\3{,}5\end{pmatrix}+s\cdot \begin{pmatrix}-13{,}5\\0\\-0{,}5\end{pmatrix}$

Der Punkt der Netzoberkante, der überquert wird, ist $V(\frac{65}{3}\mid 39\mid z_2)$ .

Der Punkt $V$ muss auf der Netzoberkante $l$ liegen:

$\begin{pmatrix}\frac{65}{3}\\39\\z_2\end{pmatrix}=\begin{pmatrix}27\\39\\3{,}5\end{pmatrix}+s\cdot \begin{pmatrix}-13{,}5\\0\\-0{,}5\end{pmatrix}$

Gleichung $\mathrm{(I)}$ lautet: $\dfrac{65}{3}=27-13{,}5\cdot s$

Auflösung nach $s$ :

$\displaystyle \dfrac{65}{3}$	$=$	$\displaystyle 27-13{,}5\cdot s$
	↓	Klammere 13,5 aus.
$\displaystyle \dfrac{65}{3}$	$=$	$\displaystyle 13{,}5\cdot(2- s)$
$\displaystyle \dfrac{65}{3}$	$=$	$\displaystyle \dfrac{27}{2}\cdot(2-s)$	$\displaystyle \cdot\dfrac{2}{27}$
$\displaystyle \dfrac{65}{3}\cdot\dfrac{2}{27}$	$=$	$\displaystyle 2-s$
$\displaystyle \dfrac{130}{81}$	$=$	$\displaystyle 2-s$	$\displaystyle +s-\dfrac{130}{81}$
$\displaystyle s$	$=$	$\displaystyle 2-\dfrac{130}{81}$
$\displaystyle s$	$=$	$\displaystyle \dfrac{32}{81}$

Mit $s=\dfrac{32}{81}$ folgt dann in Gleichung $\mathrm{(III)}$ :

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Damit hat der Punkt $V$ die Koordinaten $V\left(\frac{65}{3}\mid 39\mid \frac{535}{162}\right)$ .

Andererseits ist $U(\frac{65}{3}\mid 39\mid \frac{1}{3}h)$ :

Der Ball überquert das Netz in einer Höhe von $0{,}25\; \mathrm{ft}$ über dem Netz.

Die Differenz der z-Werte von $U$ und $V$ muss gleich $0{,}25$ sein.

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Der zugehörige Wert von $h$ ist etwa $10{,}66\; \mathrm{ft}$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

9

Aufgabe 3C

Gegeben sind der Punkt $A(2|2| 1)$ und die Gerade $g$ mit $\def\arraystretch{1.25} \vec{x}=\left(\begin{array}{c}0 \\ -2 \\ -1\end{array}\right)+s \cdot\left(\begin{array}{l}1 \\ 2 \\ 1\end{array}\right), s \in \mathbb{R}$ .

Zeigen Sie, dass $A$ ein Punkt von $g$ ist.
Die Ebene $E$ enthält den Punkt $A$ . $E$ und $g$ sind orthogonal zueinander.
Bestimmen Sie eine Gleichung für $E$ . (6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden und Ebenen im Raum
$A$ ist ein Punkt von $g$
Setze $A$ in $g$ ein:
$\begin{pmatrix}2 \\ 2 \\ 1\end{pmatrix}=\begin{pmatrix}0 \\ -2 \\ -1\end{pmatrix}+s\cdot\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$
Aus Gleichung $\mathrm{(I)}$ folgt, dass $s=2$ ist. Die zweite und dritte Gleichung sind für $s=2$ auch erfüllt. $A$ ist ein Punkt von $g$ .
Gleichung für $E$
$E$ und $g$ sind orthogonal zueinander, d.h. der Richtungsvektor der Geraden $\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$ ist der Normalenvektor der Ebene $E$ :
$E:\;\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}\circ \vec x=d$
Wegen $A\in E$ folgt: $\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}\circ \begin{pmatrix}2 \\ 2 \\ 1\end{pmatrix}=d\;\Rightarrow\;1\cdot 2+2\cdot 2+1\cdot 1=d\;\Rightarrow\;d=7$
$E:\; x+2y+z=7$ ist die gesuchte Ebenengleichung.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Setze $A$ in $g$ ein und prüfe, ob die $3$ Gleichungen für ein $s$ erfüllt sind.
$E$ und $g$ sind orthogonal zueinander, d.h. der Richtungsvektor der Geraden $\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$ ist der Normalenvektor der Ebene $E$ . Beachte auch, dass $A\in E$ ist.
Gegeben sind die Geraden $h_{a}$ mit $\def\arraystretch{1.25} \vec{x}=\left(\begin{array}{l}3 \\ 4 \\ 4\end{array}\right)+r \cdot\left(\begin{array}{c}a \\ -1 \\ 0\end{array}\right), r \in \mathbb{R}, a \in \mathbb{R}$ .
Geben Sie eine Gleichung der Ebene $H$ an, in der alle Geraden $h_{a}$ liegen.
Zeigen Sie, dass nicht jeder Punkt der Ebene $H$ auch ein Punkt von $h_{a}$ ist. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden und Ebenen im Raum
Gleichung der Ebene $H$ an, in der alle Geraden $h_{a}$ liegen
Es ist $\def\arraystretch{1.25} h_a:\;\vec{x}=\left(\begin{array}{l}3 \\ 4 \\ 4\end{array}\right)+r \cdot\left(\begin{array}{c}a \\ -1 \\ 0\end{array}\right)$
Die dritte Gleichung ist $z=4$ . Das ist auch die Gleichung der Ebene $H$ .
Überprüfung: $h_a\cap H\;\Rightarrow\;0\cdot(3+r\cdot a)+0\cdot(4-r)+4+r\cdot 0=4\;\checkmark$
Nicht jeder Punkt der Ebene $H$ ist auch ein Punkt von $h_{a}$
Wähle z.B. den Punkt $B(0|4|4)$ . Es gilt: $B\in E$ . Prüfe, ob $B\in h_a$ :
Aus Gleichung $\mathrm{(II)}$ folgt, dass $r=0$ ist.
Dann ergibt sich Gleichung $\mathrm{(I)}$ : $0=3+0\cdot a\;\Rightarrow\;0=3$
Das ist aber ein Widerspruch, sodass $B\notin h_a$ .
Damit ist gezeigt, dass nicht jeder Punkt der Ebene $H$ auch ein Punkt von $h_{a}$ ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Betrachte die dritte Gleichung der Geradengleichung.
Teil 2
Wähle einen Punkt mit den Koordinaten $(x|4|4)$ ( $x$ beliebig) und prüfe, ob dieser Punkt in der Ebene $H$ liegt.

Klassifizieren Sie die Geraden $h_{a}$ nach der Anzahl ihrer gemeinsamen Punkte mit der Ebene, mit der Gleichung $x+2 y+z=7$ . (4 BE)

Eine der Geraden von $h_{a}$ hat einen Schnittpunkt mit $g$ .

Berechnen Sie den Schnittpunkt und den Schnittwinkel. (8 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung zwischen zwei Geraden

Schnittpunkt von $h_{a}$ mit g

$h_a\cap g:$

$\displaystyle \begin{pmatrix}3 \\ 4 \\ 4\end{pmatrix}+r\cdot\begin{pmatrix}a \\ -1 \\ 0\end{pmatrix}$	$=$	$\displaystyle \begin{pmatrix}0 \\ -2 \\ -1\end{pmatrix}+s\cdot\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$	$\displaystyle -\begin{pmatrix}0 \\ -2 \\ -1\end{pmatrix}$
	↓	Bringe die Richtungsvektoren auf eine Seite der Gleichung und die Stützvektoren auf die andere Gleichungsseite.
$\displaystyle \begin{pmatrix}3 \\ 4 \\ 4\end{pmatrix}+r\cdot\begin{pmatrix}a \\ -1 \\ 0\end{pmatrix}-\begin{pmatrix}0 \\ -2 \\ -1\end{pmatrix}$	$=$	$\displaystyle s\cdot\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$	$\displaystyle -r\cdot\begin{pmatrix}a \\ -1 \\ 0\end{pmatrix}$
$\displaystyle \begin{pmatrix}3 \\ 4 \\ 4\end{pmatrix}-\begin{pmatrix}0 \\ -2 \\ -1\end{pmatrix}$	$=$	$\displaystyle s\cdot\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}-r\cdot\begin{pmatrix}a \\ -1 \\ 0\end{pmatrix}$
	↓	Berechne die Differenz.
$\displaystyle \begin{pmatrix}3 \\ 6 \\ 5\end{pmatrix}$	$=$	$\displaystyle s\cdot\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}-r\cdot\begin{pmatrix}a \\ -1 \\ 0\end{pmatrix}$

Aus der dritten Gleichung folgt $s=5$ .

In Gleichung $\mathrm{(II)}$ wird $s=5$ eingesetzt: $6=5\cdot 2+r\;\Rightarrow\;r=-4$ .

$r=-4$ und $s=5$ in Gleichung $\mathrm{(I)}$ eingesetzt ergibt: $3=5-(-4)\cdot a\;\Rightarrow\;-2=4\cdot a\;\Rightarrow\;a=-0{,}5$

Setzt man $s=5$ in $g$ ein, erhält man den Schnittpunkt der beiden Geraden:

\displaystyle \def\arraystretch{1.25} \begin{aligned}f_3(x)=0&\Leftrightarrow x(x-3)(x-2\cdot3)=0\\&\Leftrightarrow x=0\lor x-3=0\lor x-6=0\end{aligned}

Der Schnittpunkt von $h_{-0{,}5}$ mit $g$ hat die Koordinaten $S(5|8|4)$ .

Berechnen Sie den Schnittwinkel von $h_{-0{,}5}$ mit g

Der Richtungsvektor von $h_{-0{,}5}$ ist $\vec u=\begin{pmatrix}-0{,}5 \\ -1 \\ 0\end{pmatrix}$ und der Richtungsvektor von $g$ ist $\vec v=\begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}$ . Für den Schnittwinkel gilt dann:

$\displaystyle \cos \alpha$	$=$	$\displaystyle \dfrac{\|\vec u\circ \vec v\|}{\|\vec u\|\cdot \|\vec v\|}$
	$=$	$\displaystyle \dfrac{\left\|\begin{pmatrix}-0{,}5 \\ -1 \\ 0\end{pmatrix}\circ \begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix}\right\|}{\sqrt{(-0{,}5)^2+(-1)^2+0^2}\cdot \sqrt{1^2+2^2+1^2}}$
	↓	Berechne das Skalarprodukt.
	$=$	$\displaystyle \dfrac{\left\|-0{,}5-2\right\|}{\sqrt{1{,}25}\cdot \sqrt{6}}$
	↓	Berechne den Betrag.
	$=$	$\displaystyle \dfrac{2{,}5}{\sqrt{7{,}5}}$

$\alpha=\cos^{-1}\left(\dfrac{2{,}5}{\sqrt{7{,}5}}\right)\approx24{,}1^\circ$

Der Schnittwinkel zwischen den beiden Geraden beträgt rund $24{,}1^\circ$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Der Punkt $T$ bewegt sich auf der Geraden $h_{0}$ und bildet mit zwei Punkten $P$ und $Q$ auf der Geraden $g$ ein Dreieck.
Begründen Sie, dass es genau einen Punkt $T$ gibt, für den das Dreieck $P Q T$ minimalen Flächeninhalt hat. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand zweier Geraden
Begründung, dass es genau einen Punkt $T$ gibt, für den das Dreieck $P Q T$ minimalen Flächeninhalt hat
Der Punkt $T$ bewegt sich auf der Geraden $h_{0}$ . Zwei Punkte $P$ und $Q$ liegen auf der Geraden $g$ und bilden zusammen mit $T$ ein Dreieck. Die beiden Geraden $g$ und $h_0$ sind windschief.
Siehe Skizze:
Die Dreiecksfläche ist $A_{PQT}=\dfrac{1}{2}\cdot |\overline {PQ}|\cdot h$ .
Dabei ist die Höhe $h$ das Lot von $T$ auf $g$ .
Diese Höhe ist am kleinsten, wenn $T$ auf $h_0$ dort liegt, wo sich $g$ und $h_0$ am nächsten sind. Das ist dann der Fall, wenn der Abstand von $T$ und $g$ genauso groß wie der Abstand von $g$ und $h_0$ ist.
In diesem Fall hat das Dreieck $P Q T$ einen minimalen Flächeninhalt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die Dreiecksfläche ist $A_{PQT}=\dfrac{1}{2}\cdot |\overline {PQ}|\cdot h$ . Dabei ist die Höhe $h$ das Lot von $T$ auf $g$ .
Suche einen Ort für den Punkt $T$ auf $h_0$ , an dem die Höhe $h$ minimal wird.

$\displaystyle -1$	$=$	$\displaystyle f_a'(0)\cdot g_a'(0)$
	$=$	$\displaystyle \left((-a)\cdot e^{-a \cdot 0}-(-4)\cdot e^{-4\cdot0}\right)\cdot \left(-(-a)\cdot e^{-a \cdot 0}+(-4)\cdot e^{-4\cdot0}\right)$
	$=$	$\displaystyle (-a+4)\cdot(a-4)$

$\displaystyle -f_a(-x)$	$=$	$\displaystyle -(-x)(-x-a)(-x-2a)$
	↓	Aus jeder Klammer ein Minus ausklammern
	$=$	$\displaystyle x(x+a)(x+2a)$
	↓	Wir brauchen ein Minus in der Klammer, daher ersetzen wir Plus mit einem doppelten Minus
	$=$	$\displaystyle x(x-(-a))(x-(-2a))$
	↓	Dies ist genau die Form unserer Funktionenschar
	$=$	$\displaystyle f_{-a}(x)$

$\displaystyle P(\overline{FF}\cap A)$	$=$	$\displaystyle P(A)-P(FF\cap A)$
	↓	Siehe oben
	$=$	$\displaystyle P(kF\cap A)+P(FF\cap A)+P(GF\cap A)-P(FF\cap A)$
	$=$	$\displaystyle P(kF\cap A)+P(GF\cap A)$
	$=$	$\displaystyle 0{,}96\cdot0{,}005+0{,}01\cdot0{,}98$
	$=$	$\displaystyle 0{,}0146$

$\displaystyle \sqrt{8+4k^2}$	$=$	$\displaystyle 6$	$\displaystyle ()^2$
$\displaystyle 8+4k^2$	$=$	$\displaystyle 36$	$\displaystyle -8$
$\displaystyle 4k^2$	$=$	$\displaystyle 28$	$\displaystyle :4$
$\displaystyle k^2$	$=$	$\displaystyle 7$

$\displaystyle \cos60^{\circ}$	$=$	$\displaystyle \dfrac{\left\|\begin{pmatrix}0\\0\\1\end{pmatrix}\circ\begin{pmatrix}0\\k\\-1\end{pmatrix}\right\|}{1\cdot \sqrt{k^2+1}}$
	↓	Berechne das Skalarprodukt und den $\cos60^{\circ}$ .
$\displaystyle 0{,}5$	$=$	$\displaystyle \dfrac{\left\|-1\right\|}{1\cdot \sqrt{k^2+1}}$
	↓	Berechne den Betrag.
$\displaystyle 0{,}5$	$=$	$\displaystyle \dfrac{1}{\sqrt{k^2+1}}$	$\displaystyle \cdot \sqrt{k^2+1}$
$\displaystyle 0{,}5\cdot \sqrt{k^2+1}$	$=$	$\displaystyle 1$	$\displaystyle \cdot 2$
$\displaystyle \sqrt{k^2+1}$	$=$	$\displaystyle 2$	$\displaystyle ()^2$
$\displaystyle k^2+1$	$=$	$\displaystyle 4$	$\displaystyle -1$
$\displaystyle k^2$	$=$	$\displaystyle 3$

$\displaystyle \sin\alpha$	$=$	$\displaystyle \dfrac{\left\|\begin{pmatrix}13\\58{,}5\\-10{,}4\end{pmatrix}\circ \begin{pmatrix}0\\0\\1\end{pmatrix}\right\|}{\sqrt{3699{,}41}\cdot 1}$
	↓	Berechne das Skalarprodukt.
	$=$	$\displaystyle \dfrac{\left\|0+0-10{,}4\right\|}{\sqrt{3699{,}41}\cdot 1}$
	↓	Vereinfache.
	$=$	$\displaystyle \dfrac{10{,}4}{\sqrt{3699{,}41}}$

$\displaystyle (3+r\cdot a)+2\cdot(4-r)+(4+r\cdot0)$	$=$	$\displaystyle 7$
	↓	Löse die Klammern auf
$\displaystyle 3+ra+8-2r+4$	$=$	$\displaystyle 7$
	↓	Fasse zusammen.
$\displaystyle 15+r(a-2)$	$=$	$\displaystyle 7$	$\displaystyle -15$
$\displaystyle r(a-2)$	$=$	$\displaystyle -8$	$\displaystyle :(a-2)$
$\displaystyle r$	$=$	$\displaystyle \dfrac{-8}{a-2}$
	↓	Klammere im Zähler und Nenner $(-1)$ aus und kürze.
$\displaystyle r$	$=$	$\displaystyle \dfrac{8}{2-a}$

Wahlteil - CAS

Aufgabe 1A

Konzentration nach einer Stunde

Konzentration übersteigt 2,8 mgl\frac {mg}{l}lmg​

Konzentration mindestens 0,5mgl0{,}5\frac{mg}{l}0,5lmg​

Hast du eine Frage oder Feedback?

x-Koordinate der Extremstelle

Art der Extremstelle

y-Koordinate bzw. zugehörige Konzentration

Hast du eine Frage oder Feedback?

Berechnung des x-Wertes

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Tangente bestimmen

Nullstelle der Tangente

Hast du eine Frage oder Feedback?

Term für die Einnahme der zweiten Tablette

Hochpunkt des neuen Funktionsgraphen

Hast du eine Frage oder Feedback?

Integral bestimmen

Gleichung aufstellen und lösen

Hast du eine Frage oder Feedback?

Extrema in Abhängigkeit von aaa

Hast du eine Frage oder Feedback?

Wert für aaa damit sich die Graphen senkrecht schneiden

Hast du eine Frage oder Feedback?

Aufgabe 1B

Nullstellen bestimmen

Funktion umformen

Ableitungen bilden

Hochpunkt berechnen

Hast du eine Frage oder Feedback?

Erste Steigung

Zweite Steigung

Gleichsetzen

Hast du eine Frage oder Feedback?

Ableitung

Parallelität

Identisch

Hast du eine Frage oder Feedback?

Spiegelung um den Ursprung

Anwendung auf den Graphen

Hast du eine Frage oder Feedback?

Beschreibung des Dreiecks

Steigung folgern

Parameter finden

Hast du eine Frage oder Feedback?

Stammfunktion berechnen

Intervall auftrennen

Integrale berechnen

Lösen nach aaa

Hast du eine Frage oder Feedback?

Ableitungen bilden

Extremstellen finden

Tiefpunkt finden

Werte ausrechnen

Hast du eine Frage oder Feedback?

Tangente finden

Schnittpunkte finden

Erste Fläche berechnen

Zweite Fläche berechnen

Verhältnis ausrechnen

Hast du eine Frage oder Feedback?

Aufgabe 1C

Intervall, in dem der Klimadeich mindestens 5 m5 \mathrm{~m}5 m hoch ist

Entscheidung, ob der Klimadeich diese Regel (etwa fünfmal so breit wie er hoch) erfüllt

Hast du eine Frage oder Feedback?

Maximale Höhe des früheren Deiches auf cm\mathrm{cm}cm genau

Hast du eine Frage oder Feedback?

Durchschnittliche Steigung des Klimadeiches im Intervall [0;30][0; 30][0;30]

Neigungswinkel des Klimadeiches an der Stelle x=0x=0x=0

Hast du eine Frage oder Feedback?

Prozentualer Anteil des Sandkerns im Querschnitt im Bereich 5≤x≤425 \leq x \leq 425≤x≤42

Hast du eine Frage oder Feedback?

Querschnitts der Kleibodenschicht kann mit 1,5⋅(b−a)1{,}5\cdot(b-a)1,5⋅(b−a) berechnet werden

Hast du eine Frage oder Feedback?

Aufstellen der Normalen

Schnittpunkt der Normalen n(x)n(x)n(x) mit g(x)g(x)g(x)

Hast du eine Frage oder Feedback?

Näherungswert für kkk für Graph I und Graph II

Konzentration übersteigt 2,8 $\frac {mg}{l}$

Konzentration mindestens $0{,}5\frac{mg}{l}$

Extrema in Abhängigkeit von $a$

Wert für $a$ damit sich die Graphen senkrecht schneiden

Lösen nach $a$

Intervall, in dem der Klimadeich mindestens $5 \mathrm{~m}$ hoch ist

Maximale Höhe des früheren Deiches auf $\mathrm{cm}$ genau

Durchschnittliche Steigung des Klimadeiches im Intervall $[0; 30]$

Neigungswinkel des Klimadeiches an der Stelle $x=0$

Prozentualer Anteil des Sandkerns im Querschnitt im Bereich $5 \leq x \leq 42$

Querschnitts der Kleibodenschicht kann mit $1{,}5\cdot(b-a)$ berechnet werden

Schnittpunkt der Normalen $n(x)$ mit $g(x)$

Näherungswert für $k$ für Graph I und Graph II

Gibt es einen Wert für $k$ mit $41{,}5 \leq k \leq 47{,}5$ , sodass beide Bedingungen gleichzeitig erfüllt sind?

Sind die Ereignisse $A$ und $B$ stochastisch unabhängig?

Ereignis „⁣ $\bar{A}$ und $B$ " im Sachzusammenhang

Wahrscheinlichkeit, dass die Anzahl derjenigen ausgewählten Personen, die das Internet mit einem Smartphone nutzen, weniger als $10 \%$ vom Erwartungswert dieser Anzahl abweicht

Term $\frac{195-(k-w)}{300-k}$ im Sachzusammenhang

Inhalt der Oberfläche der Pyramide $A B C D S_{k}$

Koordinaten des Spiegelpunktes $S_{k}$ '

Abstand von $S_k$ zu $S_k'$ beträgt 6

Gleichung von $L$ in Koordinatenform

Größe von $k$

Das Dreieck $B S_{k} D$ soll rechtwinklig sein

Die $x$ - und die $y$ -Koordinate von $F_{k}$

Verhältnis des Volumens der Pyramide $E_{k} F_{k} G_{k} H_{k} T$ zum Volumen der Pyramide $A B C D S_{k}$

Koordinaten des Punktes $D$