Analysis, Teil B, Aufgabengruppe 2

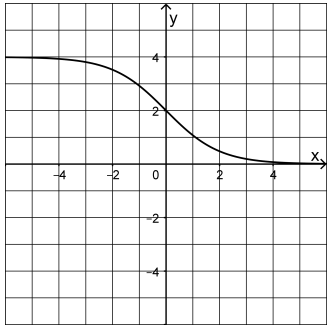
Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion

$f:x\mapsto\dfrac{4}{1+e^x}$ . Der Graph ist symmetrisch bezüglich seines Wendepunkts $(0 ∣ 2)$ .

Begründen Sie anhand des Funktionsterms von $f$ , dass $f$ keine Nullstelle hat, und geben Sie $\lim\limits_{x \rightarrow -\infty}f(x)$ sowie $\lim\limits_{x \rightarrow +\infty}f(x)$ an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Begründe anhand des Funktionsterms von $f$ , dass $f$ keine Nullstelle hat
Der Zähler von $f$ ist gleich $4$ und damit ungleich $0$ , d.h. $f$ hat keine Nullstelle.
Berechne $\lim\limits_{x \rightarrow -\infty}f(x)$ und $\lim\limits_{x \rightarrow +\infty}f(x)$
$\lim\limits_{x \rightarrow -\infty}f(x)=\lim\limits_{x \rightarrow -\infty}\dfrac{4}{1+\underbrace{e^x}_{\to 0}}=4$
$\lim\limits_{x \rightarrow +\infty}f(x)=\lim\limits_{x \rightarrow +\infty}\dfrac{4}{1+\underbrace{e^x}_{\to +\infty}}=0$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Betrachte den Zähler von $f$ . Kann er gleich null werden?
Teil 2
Beachte bei der Berechnung der Grenzwerte, wie sich die e-Funktion in Nenner verhält.
Berechnen Sie die mittlere Steigung des Graphen von $f$ im Bereich $−1\le x\le1$ auf Hundertstel genau und bestimmen Sie grafisch die Steigung des Graphen von $f$ in seinem Wendepunkt.
Berechne die mittlere Steigung des Graphen von $f$ im Bereich $−1\le x\le1$ auf Hundertstel genau
Wir verwenden die Formel für die mittlere Steigung. Hier ist $a = - 1$ und $b = 1$ , also erhalten wir:
$\overline{m}=\dfrac{f(b)-f(a)}{b-a}=\dfrac{\dfrac{4}{1+e^1}-\dfrac{4}{1+e^{-1}}}{1-(-1)}\approx-0{,}92$
Die mittlere Steigung des Graphen von $f$ im Bereich $−1\le x\le1$ beträgt rund $- 0,92$ .
Bestimme grafisch die Steigung des Graphen von $f$ in seinem Wendepunkt
Die Steigung des Graphen von $f$ in seinem Wendepunkt beträgt $m_{WP}=\frac{-2}{2}=-1$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Die mittlere Steigung ist die Steigung der Sekante: $\overline{m}=\dfrac{f(b)-f(a)}{b-a}$
Teil 2
Zeichne ein Steigungsdreieck im Wendepunkt ein.
Für die in $\mathbb{R}$ definierte erste Ableitungsfunktion $f^{'}$ von $f$ gilt $f^{'} (- x) = f^{'} (x)$ .
Geben Sie die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von $f^{'}$ an und skizzieren Sie in der Abbildung den Graphen von $f^{'}$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
Gib die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von $f^{'}$ an
Wenn $f^{'} (- x) = f^{'} (x)$ gilt, dann verläuft der Graph von $f^{'} (x)$ symmetrisch zur y-Achse.
Skizziere in der Abbildung den Graphen von $f^{'}$
Anmerkung zur Zeichnung:
Für $x \le -6$ bzw. $x \ge 6$ ist $f'(x)\approx0$ , da $f$ in diesen Bereichen nahezu gar nicht steigt oder fällt.
Für $x = 0$ ist $f^{'} (0) = - 1$ und $f^{'} (x)$ ist symmetrisch zur y-Achse.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
gTeil 1
Es gilt: Wenn $f^{'} (- x) = f^{'} (x)$ , dann ist der Graph von $f^{'} (x)$ achsen-symmetrisch zur y-Achse.
Teil 2
Die größte Steigung hat $f$ im Wendepunkt (in Aufgabe b) berechnet).
Entnimm dem Graphen von $f$ die Steigungen für $x\leq -6$ und für $x\geq 6$ .
Beachte die Symmetrie von $f^{'} (x)$ .

Betrachtet wird die in $\mathbb{R}$ definierte Funktion $F:x\mapsto4x-4\cdot \ln(e^x+1)$

Zeigen Sie, dass die Funktion $F$ eine Stammfunktion von $f$ ist.

Beurteilen Sie die folgende Aussage:
Der Graph von $F$ verläuft vollständig unterhalb der x-Achse.
Für diese Aufgabe benötigst Du folgendes Grundwissen: ln-Funktion
Der Graph von $F$ verläuft vollständig unterhalb der x-Achse
Es ist $F(x)=4x-4\cdot \ln(e^x+1)=4\cdot\left(x-\ln(e^x+1)\right)$ .
Nachdem $4 > 0$ ist, müssen wir das Vorzeichen des Terms $x - \ln(e^x + 1)$ bestimmen:
Für $x < 0$ gilt $\underbrace{x}_{<0}\underbrace{-\ln(e^x+1)}_{<0}<0$ , denn hier ist $\ln(e^x+1)>\ln(1)=0$ und daher $-\ln(e^x+1)<0$ .
Für $x = 0$ ist $0-\ln(e^0+1)=-\ln(2)<0$ .
Für $x > 0$ gilt $\underbrace{x-\underbrace{\ln(e^x+1)}_{>x}}_{<0}<0$ , denn hier ist $\ln(e^x+1)>\ln(e^x)=x$ und daher $-\ln(e^x+1)<x$ .
Also ist für alle $x$ der Term $4\cdot\left(x-\ln(e^x+1)\right)<0$ und der Graph von $F$ verläuft vollständig unterhalb der $x$ -Achse.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Es ist $F(x)=4\cdot\left(x-\ln(e^x+1)\right)$ .
Betrachte das Vorzeichen des Terms $x-\ln(e^x+1)$ , wenn $x$ verschiedene Werte annimmt.
Begründen Sie, dass der Wert des Integrals $\displaystyle\int_{-k}^{k}f(x) \;\mathrm{d}x$ für jede positive reelle Zahl $k$ ohne Verwendung einer Stammfunktion von $f$ exakt bestimmt werden kann, und geben Sie den Wert des Integrals an.
Bestimmung des Werts des Integrals ohne Stammfunktion
Der konkrete Fall $k = 2$
Gezeichnet ist in der Abbildung das Integral $\displaystyle\int_{-2}^{2}f(x) \;\mathrm{d}x= \textcolor{ff6600}{ A_1 }+\textcolor{006400}{ A_2 }$ , wobei
$\textcolor{ff6600}{ A_1 }=\displaystyle\int_{-2}^{0}f(x) \;\mathrm{d}x$ und $\textcolor{006400}{ A_2 } =\displaystyle\int_{0}^{2}f(x) \;\mathrm{d}x$ .
Wegen der Punktsymmetrie zum Wendepunkt kann die Fläche $\textcolor{006400}{ A_2 }$ auch oberhalb von $\textcolor{ff6600}{ A_1 }$ angeordnet werden, sodass sich für $\textcolor{ff6600}{ A_1 }+\textcolor{006400}{ A_2 } =2\cdot 4=8$ ergibt.
Der allgemeine Fall
Oben war $k = 2$ . Wenn nun $k$ ein anderer Wert wäre, so könnten völlig analog die Flächen unter dem Graphen von $f$ von $- k$ bis $0$ und von $0$ bis $k$ übereinander gelegt werden, um ein Rechteck zu erhalten.
Der wichtige Schritt ist nun, zu erkennen, dass die Höhe des entstehenden Rechtecks immer $4$ ist, ganz unabhängig davon, welcher Wert für $k$ gewählt wurde, während die Breite des Rechtecks durch $k$ gegeben ist. Also ist allgemein die berechnete Fläche gleich $k\cdot4$ .
Aus dieser Überlegung folgt bereits der Wert des Integrals:
$\displaystyle\int_{-k}^{k}f(x) \;\mathrm{d}x=4k.$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Betrachte eventuell zunächst einen konkreten Fall wie $k = 2$ .
Teile das Integral auf in $\int_{-2}^0 f(x) \;\mathrm{d}x$ und $\int_0^2 f(x)\;\mathrm{d}x$ .
Überlege dir nun, wie Du die zu den Integralen gehörigen Flächen geschickt anordnen kannst, um leicht ihren gemeinsamen Flächeninhalt berechnen zu können.
Funktioniert Deine Methode auch für ein allgemeines $k$ ? Was musst Du ändern oder anpassen?

$\displaystyle F(x)$	$=$	$\displaystyle 4x-4\cdot \ln(e^x+1)$
	↓	Leite ab, beachte die Kettenregel.
$\displaystyle F'(x)$	$=$	$\displaystyle 4-4\cdot\dfrac{1}{e^x+1}\cdot e^x$
	↓	Vereinfache.
	$=$	$\displaystyle 4-\dfrac{4\cdot e^x}{e^x+1}$
	↓	Bringe auf gemeinsamen Nenner.
	$=$	$\displaystyle \dfrac{4\cdot(e^x+1)-4\cdot e^x}{e^x+1}$
	↓	Löse die Klammer auf.
	$=$	$\displaystyle \dfrac{4\cdot e^x+4-4\cdot e^x}{e^x+1}$
	↓	Vereinfache den Zähler.
	$=$	$\displaystyle \dfrac{4}{e^x+1}$

Begründe anhand des Funktionsterms von fff, dass fff keine Nullstelle hat

Berechne lim⁡x→−∞f(x)\lim\limits_{x \rightarrow -\infty}f(x)x→−∞lim​f(x) und lim⁡x→+∞f(x)\lim\limits_{x \rightarrow +\infty}f(x)x→+∞lim​f(x)

Hast du eine Frage oder Feedback?

Berechne die mittlere Steigung des Graphen von fff im Bereich −1≤x≤1−1\le x\le1−1≤x≤1 auf Hundertstel genau

Bestimme grafisch die Steigung des Graphen von fff in seinem Wendepunkt

Hast du eine Frage oder Feedback?

Gib die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von f′f'f′ an

Skizziere in der Abbildung den Graphen von f′f'f′

Hast du eine Frage oder Feedback?

Zeige, dass die Funktion FFF eine Stammfunktion von fff ist

Hast du eine Frage oder Feedback?

Der Graph von FFF verläuft vollständig unterhalb der x-Achse

Hast du eine Frage oder Feedback?

Bestimmung des Werts des Integrals ohne Stammfunktion

Der konkrete Fall k=2k = 2k=2

Der allgemeine Fall

Hast du eine Frage oder Feedback?

Begründe anhand des Funktionsterms von $f$ , dass $f$ keine Nullstelle hat

Berechne $\lim\limits_{x \rightarrow -\infty}f(x)$ und $\lim\limits_{x \rightarrow +\infty}f(x)$

Berechne die mittlere Steigung des Graphen von $f$ im Bereich $−1\le x\le1$ auf Hundertstel genau

Bestimme grafisch die Steigung des Graphen von $f$ in seinem Wendepunkt

Gib die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von $f^{'}$ an

Skizziere in der Abbildung den Graphen von $f^{'}$

Zeige, dass die Funktion $F$ eine Stammfunktion von $f$ ist

Der Graph von $F$ verläuft vollständig unterhalb der x-Achse

Der konkrete Fall $k = 2$