Analysis, Teil B, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Bei der Bearbeitung der Aufgaben dürfen als Hilfsmittel verwendet werden.

• die vom Staatsministerium genehmigte Merkhilfe für das Fach Mathematik,

• eine der vom Staatsministerium zugelassenen stochastischen Tabellen,

• eine der vom Staatsministerium für Leistungserhebungen zugelassenen naturwissenschaftlichen Formelsammlungen,

• ein Taschenrechner, der den vom Staatsministerium getroffenen Regelungen

entspricht.

Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion

$f:x\mapsto\dfrac{4}{1+e^x}$ . Der Graph ist symmetrisch bezüglich seines Wendepunkts $(0 ∣ 2)$ .

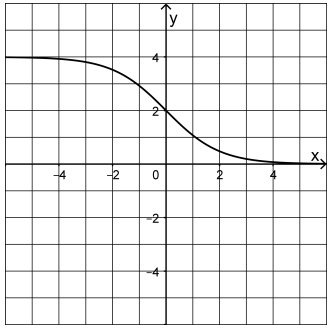
Begründen Sie anhand des Funktionsterms von $f$ , dass $f$ keine Nullstelle hat, und geben Sie $\lim\limits_{x \rightarrow -\infty}f(x)$ sowie $\lim\limits_{x \rightarrow +\infty}f(x)$ an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Begründe anhand des Funktionsterms von $f$ , dass $f$ keine Nullstelle hat
Der Zähler von $f$ ist gleich $4$ und damit ungleich $0$ , d.h. $f$ hat keine Nullstelle.
Berechne $\lim\limits_{x \rightarrow -\infty}f(x)$ und $\lim\limits_{x \rightarrow +\infty}f(x)$
$\lim\limits_{x \rightarrow -\infty}f(x)=\lim\limits_{x \rightarrow -\infty}\dfrac{4}{1+\underbrace{e^x}_{\to 0}}=4$
$\lim\limits_{x \rightarrow +\infty}f(x)=\lim\limits_{x \rightarrow +\infty}\dfrac{4}{1+\underbrace{e^x}_{\to +\infty}}=0$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Betrachte den Zähler von $f$ . Kann er gleich null werden?
Teil 2
Beachte bei der Berechnung der Grenzwerte, wie sich die e-Funktion in Nenner verhält.
Berechnen Sie die mittlere Steigung des Graphen von $f$ im Bereich $−1\le x\le1$ auf Hundertstel genau und bestimmen Sie grafisch die Steigung des Graphen von $f$ in seinem Wendepunkt.
Berechne die mittlere Steigung des Graphen von $f$ im Bereich $−1\le x\le1$ auf Hundertstel genau
Wir verwenden die Formel für die mittlere Steigung. Hier ist $a = - 1$ und $b = 1$ , also erhalten wir:
$\overline{m}=\dfrac{f(b)-f(a)}{b-a}=\dfrac{\dfrac{4}{1+e^1}-\dfrac{4}{1+e^{-1}}}{1-(-1)}\approx-0{,}92$
Die mittlere Steigung des Graphen von $f$ im Bereich $−1\le x\le1$ beträgt rund $- 0,92$ .
Bestimme grafisch die Steigung des Graphen von $f$ in seinem Wendepunkt
Die Steigung des Graphen von $f$ in seinem Wendepunkt beträgt $m_{WP}=\frac{-2}{2}=-1$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Die mittlere Steigung ist die Steigung der Sekante: $\overline{m}=\dfrac{f(b)-f(a)}{b-a}$
Teil 2
Zeichne ein Steigungsdreieck im Wendepunkt ein.
Für die in $\mathbb{R}$ definierte erste Ableitungsfunktion $f^{'}$ von $f$ gilt $f^{'} (- x) = f^{'} (x)$ .
Geben Sie die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von $f^{'}$ an und skizzieren Sie in der Abbildung den Graphen von $f^{'}$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
Gib die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von $f^{'}$ an
Wenn $f^{'} (- x) = f^{'} (x)$ gilt, dann verläuft der Graph von $f^{'} (x)$ symmetrisch zur y-Achse.
Skizziere in der Abbildung den Graphen von $f^{'}$
Anmerkung zur Zeichnung:
Für $x \le -6$ bzw. $x \ge 6$ ist $f'(x)\approx0$ , da $f$ in diesen Bereichen nahezu gar nicht steigt oder fällt.
Für $x = 0$ ist $f^{'} (0) = - 1$ und $f^{'} (x)$ ist symmetrisch zur y-Achse.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
gTeil 1
Es gilt: Wenn $f^{'} (- x) = f^{'} (x)$ , dann ist der Graph von $f^{'} (x)$ achsen-symmetrisch zur y-Achse.
Teil 2
Die größte Steigung hat $f$ im Wendepunkt (in Aufgabe b) berechnet).
Entnimm dem Graphen von $f$ die Steigungen für $x\leq -6$ und für $x\geq 6$ .
Beachte die Symmetrie von $f^{'} (x)$ .

Betrachtet wird die in $\mathbb{R}$ definierte Funktion $F:x\mapsto4x-4\cdot \ln(e^x+1)$

Zeigen Sie, dass die Funktion $F$ eine Stammfunktion von $f$ ist.

Beurteilen Sie die folgende Aussage:
Der Graph von $F$ verläuft vollständig unterhalb der x-Achse.
Für diese Aufgabe benötigst Du folgendes Grundwissen: ln-Funktion
Der Graph von $F$ verläuft vollständig unterhalb der x-Achse
Es ist $F(x)=4x-4\cdot \ln(e^x+1)=4\cdot\left(x-\ln(e^x+1)\right)$ .
Nachdem $4 > 0$ ist, müssen wir das Vorzeichen des Terms $x - \ln(e^x + 1)$ bestimmen:
Für $x < 0$ gilt $\underbrace{x}_{<0}\underbrace{-\ln(e^x+1)}_{<0}<0$ , denn hier ist $\ln(e^x+1)>\ln(1)=0$ und daher $-\ln(e^x+1)<0$ .
Für $x = 0$ ist $0-\ln(e^0+1)=-\ln(2)<0$ .
Für $x > 0$ gilt $\underbrace{x-\underbrace{\ln(e^x+1)}_{>x}}_{<0}<0$ , denn hier ist $\ln(e^x+1)>\ln(e^x)=x$ und daher $-\ln(e^x+1)<x$ .
Also ist für alle $x$ der Term $4\cdot\left(x-\ln(e^x+1)\right)<0$ und der Graph von $F$ verläuft vollständig unterhalb der $x$ -Achse.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es ist $F(x)=4\cdot\left(x-\ln(e^x+1)\right)$ .
Betrachte das Vorzeichen des Terms $x-\ln(e^x+1)$ , wenn $x$ verschiedene Werte annimmt.
Begründen Sie, dass der Wert des Integrals $\displaystyle\int_{-k}^{k}f(x) \;\mathrm{d}x$ für jede positive reelle Zahl $k$ ohne Verwendung einer Stammfunktion von $f$ exakt bestimmt werden kann, und geben Sie den Wert des Integrals an.
Bestimmung des Werts des Integrals ohne Stammfunktion
Der konkrete Fall $k = 2$
Gezeichnet ist in der Abbildung das Integral $\displaystyle\int_{-2}^{2}f(x) \;\mathrm{d}x= \textcolor{ff6600}{ A_1 }+\textcolor{006400}{ A_2 }$ , wobei
$\textcolor{ff6600}{ A_1 }=\displaystyle\int_{-2}^{0}f(x) \;\mathrm{d}x$ und $\textcolor{006400}{ A_2 } =\displaystyle\int_{0}^{2}f(x) \;\mathrm{d}x$ .
Wegen der Punktsymmetrie zum Wendepunkt kann die Fläche $\textcolor{006400}{ A_2 }$ auch oberhalb von $\textcolor{ff6600}{ A_1 }$ angeordnet werden, sodass sich für $\textcolor{ff6600}{ A_1 }+\textcolor{006400}{ A_2 } =2\cdot 4=8$ ergibt.
Der allgemeine Fall
Oben war $k = 2$ . Wenn nun $k$ ein anderer Wert wäre, so könnten völlig analog die Flächen unter dem Graphen von $f$ von $- k$ bis $0$ und von $0$ bis $k$ übereinander gelegt werden, um ein Rechteck zu erhalten.
Der wichtige Schritt ist nun, zu erkennen, dass die Höhe des entstehenden Rechtecks immer $4$ ist, ganz unabhängig davon, welcher Wert für $k$ gewählt wurde, während die Breite des Rechtecks durch $k$ gegeben ist. Also ist allgemein die berechnete Fläche gleich $k\cdot4$ .
Aus dieser Überlegung folgt bereits der Wert des Integrals:
$\displaystyle\int_{-k}^{k}f(x) \;\mathrm{d}x=4k.$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Betrachte eventuell zunächst einen konkreten Fall wie $k = 2$ .
Teile das Integral auf in $\int_{-2}^0 f(x) \;\mathrm{d}x$ und $\int_0^2 f(x)\;\mathrm{d}x$ .
Überlege dir nun, wie Du die zu den Integralen gehörigen Flächen geschickt anordnen kannst, um leicht ihren gemeinsamen Flächeninhalt berechnen zu können.
Funktioniert Deine Methode auch für ein allgemeines $k$ ? Was musst Du ändern oder anpassen?

Betrachtet wird die Schar der in $\mathbb{R}$ definierten Funktionen $w_{a;b;c}:x\mapsto\dfrac{a}{b+e^{cx}}$

mit $a,b \in \mathbb{R^+}$ und $c \in\mathbb{R}$ . Die Funktion aus Aufgabe 1 ist eine Funktion dieser Schar.

Jeder der abgebildeten Graphen I, II und III der Schar gehört, bei festen
Werten von $a$ und $b$ , zu einem der Werte $c = - 1$ , $c = 0$ und $c = 1$ .
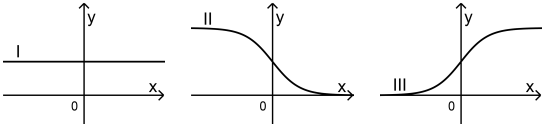
Ordnen Sie den Graphen die genannten Werte von $c$ zu und begründen
Sie Ihre Zuordnung.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wachstumsprozesse - eine Übersicht
Ordne den Graphen die genannten Werte von $c$ zu und begründe Deine Zuordnung
Für $c = - 1$ ist $w_{a;b;-1}(x)=\dfrac{a}{b+e^{-1x}}$ .
Betrachtet man die e-Funktion im Nenner, dann gilt:
$\lim\limits_{x\to +\infty}e^{-1x}=0\;\Rightarrow\;\lim\limits_{x\to +\infty}w_{a;b;-1}(x)=\dfrac{a}{b}$ , der Graph nähert sich einem konstanten Wert.
$\lim\limits_{x\to -\infty}e^{-1x}=\infty\;\Rightarrow\;\lim\limits_{x\to -\infty}w_{a;b;-1}(x)=0$ , der Graph nähert sich der x-Achse.
Damit gehört Graph III zu $c = - 1$ .
Für $c = 0$ ist $w_{a;b;0}(x)=\dfrac{a}{b+e^{0\cdot x}}=\dfrac{a}{b+1}$ eine Konstante.
Damit gehört Graph I zu $c = 0$ .
Für $c = 1$ ist $w_{a;b;1}(x)=\dfrac{a}{b+e^{1x}}$ .
Betrachtet man die e-Funktion im Nenner, dann gilt:
$\lim\limits_{x\to +\infty}e^{1x}=\infty\;\Rightarrow\;\lim\limits_{x\to +\infty}w_{a;b;1}(x)=0$ , der Graph nähert sich der x-Achse.
$\lim\limits_{x\to -\infty}e^{1x}=0\;\Rightarrow\;\lim\limits_{x\to -\infty}w_{a;b;1}(x)=\dfrac{a}{b}$ , der Graph nähert sich einem konstanten Wert.
Damit gehört Graph II zu $c = 1$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Setze nacheinander die drei gegebenen Werte für $c$ in die Funktion $w_{a;b;c}(x)$ ein.
Untersuche jeweils, wie sich die e-Funktion im Nenner für $x\to +\infty$ bzw. $x\to -\infty$ verhält und überlege dir, was dies für das Verhalten von $w (x)$ bedeutet.
Schließe auf den zugehörigen Graphen.

Auf einer Inselgruppe wurden Seeadler neu angesiedelt. Betrachtet wird die anschließende Entwicklung der Anzahl der Seeadler. In einem Modell wird diese Entwicklung mithilfe des Graphen der Funktion $w_{40;1;-0{,}2}$ beschrieben, die im Folgenden mit $w$ bezeichnet wird. Es gilt also $w(x)=\dfrac{40}{1+e^{-0{,}2x}}$ . Dabei ist $x$ die seit der Ansiedlung vergangene Zeit in Jahren und $w (x)$ die Anzahl der Seeadler.

Geben Sie auf Grundlage des Modells an, wie viele Seeadler angesiedelt wurden, und berechnen Sie, nach wie vielen Jahren die Anzahl der Seeadler auf $32$ angewachsen ist.

Die Tangente an den Graphen von $w$ im Punkt $(0 ∣ w (0))$ hat die Steigung $2$ . Würde die Entwicklung der Anzahl der Seeadler im Modell mithilfe dieser Tangente beschrieben werden, so ergäbe sich für den Zeitpunkt vier Jahre nach der Ansiedlung eine bestimmte Anzahl von Seeadlern. Untersuchen Sie, ob diese Anzahl mit derjenigen übereinstimmt, die sich bei einer Beschreibung mithilfe des Graphen von $w$ ergeben würde.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Untersuche, ob diese Anzahl mit derjenigen übereinstimmt, die sich bei einer Beschreibung mithilfe des Graphen von $w$ ergeben würde
Der Punkt $(0 ∣ w (0))$ ist gleich $(0 ∣ 20)$ . Durch diesen Punkt verläuft die Tangente und hat die Steigung $2$ .
$\Rightarrow\;t:y=2\cdot x+20$
Für $x = 4$ ist $y=2\cdot 4+20=28$ .
Nach $4$ Jahren wären mit dem Modell Tangente $28$ Seeadler vorhanden.
Berechne $w (4)$ :
$w(4)=\dfrac{40}{1+e^{-0{,}2\cdot 4}}=\dfrac{40}{1+e^{-0{,}8}}\approx27{,}6$
Da es nur "ganze" Seeadler gibt, sind mit diesem Modell ebenfalls $28$ Seeadler vorhanden.
Die beiden Anzahlen stimmen überein.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme mit den Angaben die Gleichung der Tangente und berechne den y-Wert für $x = 4$ .
Berechne $w (4)$ und vergleiche die beiden berechneten Werte.
Unter bestimmten anderen Gegebenheiten auf der Inselgruppe kann die
Entwicklung der Anzahl der Seeadler im Modell mithilfe des Graphen einer
anderen Funktion aus der Schar der Funktionen $w_{a;b;c}$ beschrieben
werden. Das folgende Gleichungssystem ermöglicht die Bestimmung der
zugehörigen Werte von $a, b$ und $c$ .
(1) $\dfrac{a}{b+1}=20\qquad$ (2) $\lim\limits_{x\to +\infty}\dfrac{a}{b+e^{cx}}=45\qquad$ (3) $\dfrac{a}{b+e^{15c}}=35$
Interpretieren Sie jede der drei Gleichungen im Sachzusammenhang.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wachstumsprozesse - eine Übersicht
Interpretiere jede der drei Gleichungen im Sachzusammenhang
(1) $\;\dfrac{a}{b+1}=20$
Die Gleichung erhält man, wenn man $w (0)$ berechnet.
Die Gleichung gibt also die Anfangszahl der neu angesiedelten Seeadler wieder.
Zu Beginn wurden 20 Seeadler angesiedelt.
(2) $\; \lim\limits_{x\to +\infty}\dfrac{a}{b+e^{cx}}=45$
Mit dieser Gleichung ermittelt man die Zahl der Seeadler nach einer sehr langen vergangenen Zeit.
Nach sehr langer Zeit sind $45$ Seeadler vorhanden.
(3) $\;\dfrac{a}{b+e^{15c}}=35$
Hier wurde in die Funktion, die die Anzahl der Adler angibt, der $x$ -Wert $15$ eingesetzt, was im Sachzusammenhang $15$ Jahren entspricht.
Die Gleichung besagt also, dass sich nach $15$ Jahren $35$ Seeadler auf der Inselgruppe befinden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Gleichung (1):
Der Term der e-Funktion $e^{c x}$ im Nenner hat hier den Wert $1$ . Was folgt daraus für den eingesetzten $x$ -Wert und was beschreibt dieser im Sachzusammenhang?
Gleichung (2):
Der Grenzwert gibt an, wie viele Seeadler nach langer Zeit vorhanden sind.
Gleichung (3):
Im Nenner ist $x = 15$ eingesetzt. Erinnere dich daran, was $x$ und $w$ angeben und Folgere damit, wofür der Term $w(15)=\frac{a}{b+e^{15 c}}$ steht.

Ermitteln Sie die Werte von $a$ und $b$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle F(x)$	$=$	$\displaystyle 4x-4\cdot \ln(e^x+1)$
	↓	Leite ab, beachte die Kettenregel.
$\displaystyle F'(x)$	$=$	$\displaystyle 4-4\cdot\dfrac{1}{e^x+1}\cdot e^x$
	↓	Vereinfache.
	$=$	$\displaystyle 4-\dfrac{4\cdot e^x}{e^x+1}$
	↓	Bringe auf gemeinsamen Nenner.
	$=$	$\displaystyle \dfrac{4\cdot(e^x+1)-4\cdot e^x}{e^x+1}$
	↓	Löse die Klammer auf.
	$=$	$\displaystyle \dfrac{4\cdot e^x+4-4\cdot e^x}{e^x+1}$
	↓	Vereinfache den Zähler.
	$=$	$\displaystyle \dfrac{4}{e^x+1}$

$\displaystyle 32$	$=$	$\displaystyle \dfrac{40}{1+e^{-0{,}2x}}$	$\displaystyle \cdot(1+e^{-0{,}2x})$
	↓	Bringe den Nenner auf die andere Seite.
$\displaystyle 32\cdot(1+e^{-0{,}2x})$	$=$	$\displaystyle 40$	$\displaystyle :32$
$\displaystyle 1+e^{-0{,}2x}$	$=$	$\displaystyle \dfrac{40}{32}$
	↓	Kürze.
$\displaystyle 1+e^{-0{,}2x}$	$=$	$\displaystyle \dfrac{5}{4}$	$\displaystyle -1$
$\displaystyle e^{-0{,}2x}$	$=$	$\displaystyle \dfrac{1}{4}$	$\displaystyle \ln()$
	↓	Benutze die ln-Funktion.
$\displaystyle -0{,}2x$	$=$	$\displaystyle \ln(0{,}25)$	$\displaystyle :(-0{,}2)$
$\displaystyle x$	$=$	$\displaystyle \dfrac{\ln(0{,}25)}{-0{,}2}$
	$\approx ≈$	$\displaystyle 6{,}9$

$\displaystyle \dfrac{a}{b+1}$	$=$	$\displaystyle 20$
	↓	Setze $a=45\cdot b$ ein.
$\displaystyle \dfrac{45\cdot b}{b+1}$	$=$	$\displaystyle 20$	$\displaystyle \cdot (b+1)$
$\displaystyle 45\cdot b$	$=$	$\displaystyle 20\cdot (b+1)$
	↓	Löse die Klammer auf.
$\displaystyle 45\cdot b$	$=$	$\displaystyle 20\cdot b+20$	$\displaystyle -20\cdot b$
$\displaystyle 25\cdot b$	$=$	$\displaystyle 20$	$\displaystyle :25$
$\displaystyle b$	$=$	$\displaystyle 0{,}8$

Analysis, Teil B, Aufgabengruppe 2

Begründe anhand des Funktionsterms von $f$ , dass $f$ keine Nullstelle hat

Berechne $\lim\limits_{x \rightarrow -\infty}f(x)$ und $\lim\limits_{x \rightarrow +\infty}f(x)$

Hast du eine Frage oder Feedback?

Berechne die mittlere Steigung des Graphen von $f$ im Bereich $−1\le x\le1$ auf Hundertstel genau

Bestimme grafisch die Steigung des Graphen von $f$ in seinem Wendepunkt

Hast du eine Frage oder Feedback?

Gib die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von $f^{'}$ an

Skizziere in der Abbildung den Graphen von $f^{'}$

Hast du eine Frage oder Feedback?

Zeige, dass die Funktion $F$ eine Stammfunktion von $f$ ist

Hast du eine Frage oder Feedback?

Der Graph von $F$ verläuft vollständig unterhalb der x-Achse

Hast du eine Frage oder Feedback?

Bestimmung des Werts des Integrals ohne Stammfunktion

Der konkrete Fall $k = 2$

Der allgemeine Fall

Hast du eine Frage oder Feedback?

Ordne den Graphen die genannten Werte von $c$ zu und begründe Deine Zuordnung

Hast du eine Frage oder Feedback?

Wie viele Seeadler wurden angesiedelt

Berechne, nach wie vielen Jahren die Anzahl der Seeadler auf $32$ angewachsen ist

Hast du eine Frage oder Feedback?

Untersuche, ob diese Anzahl mit derjenigen übereinstimmt, die sich bei einer Beschreibung mithilfe des Graphen von $w$ ergeben würde

Hast du eine Frage oder Feedback?

Interpretiere jede der drei Gleichungen im Sachzusammenhang

Hast du eine Frage oder Feedback?

Ermittele die Werte von $a$ und $b$

Hast du eine Frage oder Feedback?

Analysis, Teil B, Aufgabengruppe 2

Begründe anhand des Funktionsterms von fff, dass fff keine Nullstelle hat

Berechne lim⁡x→−∞f(x)\lim\limits_{x \rightarrow -\infty}f(x)x→−∞lim​f(x) und lim⁡x→+∞f(x)\lim\limits_{x \rightarrow +\infty}f(x)x→+∞lim​f(x)

Hast du eine Frage oder Feedback?

Berechne die mittlere Steigung des Graphen von fff im Bereich −1≤x≤1−1\le x\le1−1≤x≤1 auf Hundertstel genau

Bestimme grafisch die Steigung des Graphen von fff in seinem Wendepunkt

Hast du eine Frage oder Feedback?

Gib die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von f′f'f′ an

Skizziere in der Abbildung den Graphen von f′f'f′

Hast du eine Frage oder Feedback?

Zeige, dass die Funktion FFF eine Stammfunktion von fff ist

Hast du eine Frage oder Feedback?

Der Graph von FFF verläuft vollständig unterhalb der x-Achse

Hast du eine Frage oder Feedback?

Bestimmung des Werts des Integrals ohne Stammfunktion

Der konkrete Fall k=2k = 2k=2

Der allgemeine Fall

Hast du eine Frage oder Feedback?

Ordne den Graphen die genannten Werte von ccc zu und begründe Deine Zuordnung

Hast du eine Frage oder Feedback?

Wie viele Seeadler wurden angesiedelt

Berechne, nach wie vielen Jahren die Anzahl der Seeadler auf 323232 angewachsen ist

Hast du eine Frage oder Feedback?

Untersuche, ob diese Anzahl mit derjenigen übereinstimmt, die sich bei einer Beschreibung mithilfe des Graphen von w ww ergeben würde

Hast du eine Frage oder Feedback?

Interpretiere jede der drei Gleichungen im Sachzusammenhang

Hast du eine Frage oder Feedback?

Ermittele die Werte von aaa und bbb

Hast du eine Frage oder Feedback?

Begründe anhand des Funktionsterms von $f$ , dass $f$ keine Nullstelle hat

Berechne $\lim\limits_{x \rightarrow -\infty}f(x)$ und $\lim\limits_{x \rightarrow +\infty}f(x)$

Berechne die mittlere Steigung des Graphen von $f$ im Bereich $−1\le x\le1$ auf Hundertstel genau

Bestimme grafisch die Steigung des Graphen von $f$ in seinem Wendepunkt

Gib die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von $f^{'}$ an

Skizziere in der Abbildung den Graphen von $f^{'}$

Zeige, dass die Funktion $F$ eine Stammfunktion von $f$ ist

Der Graph von $F$ verläuft vollständig unterhalb der x-Achse

Der konkrete Fall $k = 2$

Ordne den Graphen die genannten Werte von $c$ zu und begründe Deine Zuordnung

Berechne, nach wie vielen Jahren die Anzahl der Seeadler auf $32$ angewachsen ist

Untersuche, ob diese Anzahl mit derjenigen übereinstimmt, die sich bei einer Beschreibung mithilfe des Graphen von $w$ ergeben würde

Ermittele die Werte von $a$ und $b$