In der folgenden Abbildung sind verschiedene Flächen farblich markiert.

Es soll beurteilt werden, ob der Wert des Integrals $${\displaystyle {\int }_{-2}^{8}g(x)\mathrm{d}x}$$ negativ ist.

Dazu wurde das Integrationsintervall $[-2;8]$ in mehrere Abschnitte eingeteilt.

Die beiden $\text{lilafarbigen }$Flächeninhalte $A_1$ sind gleich groß.

Ebenso gleich groß sind die beiden $\text{türkisfarbigen }$Flächeninhalte $A_3$.

Die $\text{lilafarbige }$Fläche $A_1$ und die $\text{türkisfarbige }$Fläche $A_3$ sind in die $\text{orangefarbige }$ Fläche $A_2$ eingezeichnet. Man sieht, dass die $\text{orangefarbige }$Fläche $A_2$ größer ist als die Summe der beiden Flächen $A_1$ und $A_3$. Demnach ist der Wert des Integrals nicht negativ, sondern positiv.

Antwort: Der Wert des Integrals ist nicht negativ, sondern positiv.

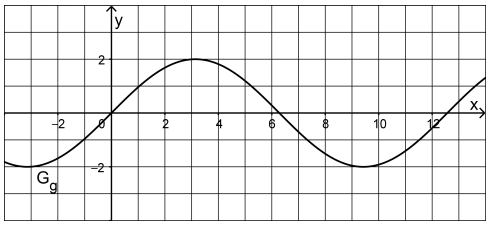
allgemeine Tangentengleichung: $t:y=m\cdot x+b$

Die Tangente an $G_g$ im Koordinatenursprung hat die selbe Steigung wie $G_g$.

Berechne die Steigung von $G_g$ im Koordinatenursprung:

$g(x)=2\cdot \sin \left({\displaystyle \frac{1}{2}}x\right)\Rightarrow g^{\prime }(x)=2\cdot \cos \left({\displaystyle \frac{1}{2}}x\right)\cdot {\displaystyle \frac{1}{2}}=\cos \left({\displaystyle \frac{1}{2}}x\right)$

Im Koordinatenursprung ist $x=0\Rightarrow$$g^{\prime }(0)=\cos (0)=1$

$\Rightarrow$ $m=0$

Da die Tangente durch den Koordinatenursprung verläuft, ist $b=0$.

Demnach erhält man für die Tangente $t$ im Koordinatenursprung die Gleichung $t:y=1\cdot x.$

Damit die beiden Punkte auf t liegen, muss die Tangentengleichung erfüllt sein, wenn man die Punkte einsetzt:

$(-1|-1):-1=1\cdot -1$

$(1|1):1=1\cdot 1$

$\Rightarrow$ Die beiden Punkte $(-1|-1)$ und $(1|1)$ liegen auf $t$.

Antwort: Die Aussage trifft zu.