Analysis, Teil A, Aufgabengruppe 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden.
- 1
Gegeben ist die in definierte Funktion mit der Ableitungsfunktion .
Berechnen Sie .
Bestimmen Sie einen Term derjenigen Stammfunktion von , deren
Graph durch den Punkt verläuft.
- 2
Die Abbildung zeigt den Graphen der in definierten Funktion mit
.
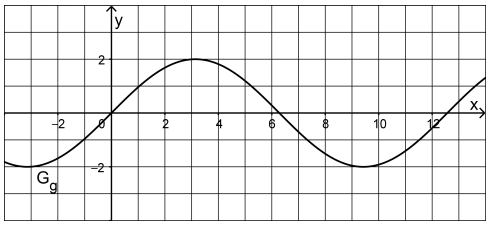
Beurteilen Sie mithilfe der Abbildung, ob der Wert des Integrals
negativ ist.
Weisen Sie rechnerisch nach, dass die folgende Aussage zutrifft:
Die Tangente an im Koordinatenursprung ist die Gerade durch die Punkte und .
- 3
Betrachtet wird die Schar der in definierten Funktionen mit und . Für jeden Wert von besitzt die Funktion genau eine Extremstelle.
Begründen Sie, dass der Graph von für unterhalb der x-Achse
verläuft.
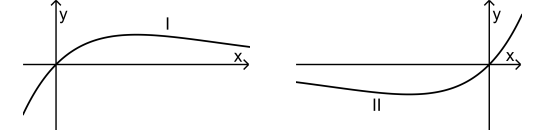
Die abgebildeten Graphen I und II sind Graphen der Schar; einer der
beiden gehört zu einem positiven Wert von . Entscheiden Sie, welcher
Graph dies ist, und begründen Sie Ihre Entscheidung.
- 4
Lösen Sie die folgenden beiden Aufgaben.
Geben Sie einen Term einer in definierten Funktion an, die den Wertebereich hat.
Geben Sie einen Term einer in definierten Funktion an, sodass der Term genau für definiert ist. Erläutern Sie die Ihrer Angabe zugrunde liegenden Überlegungen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

