Nachtermin Teil B - lernen mit Serlo!

Aufgabe B 1

Rauten $A B_{n} C D_{n}$ besitzen die gemeinsame Diagonale $\overline{AC}$ . Die Winkel $\sphericalangle CB_nA$ haben das Maß $\varphi$ mit $\varphi \in\;]0^\circ;180^\circ[$ .

Es gilt: $\overline{AC} =5\;\mathrm{cm}$ .

Die Zeichnung zeigt die Raute $A B_{1} C D_{1}$ mit den Diagonalen $\overline{AC}$ und $\overline{B_1D_1 }$ für $\varphi= 110^\circ$ .

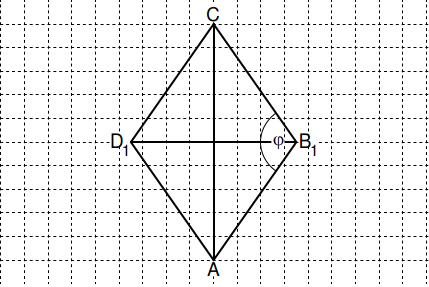
Zeichnen Sie die Raute $A B_{2} C D_{2}$ für $\varphi=80^\circ$ in die Zeichnung zur Aufgabenstellung ein. (1 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Raute
Die beiden Symmetrieachsen der Raute sollen die Koordinatenachsen sein. Dann liegt die Mitte der Raute im Koordinatenursprung.
Berechnung der Länge der halben Diagonalen $\overline{D_2B_2}$ ,
Für die Zeichnung werden z.B. die Koordinaten des Punktes $B_{2}$ benötigt.
Skizze des rechten oberen Dreiecks:
Dann gilt:
$\tan 40^\circ=\dfrac{2{,}5}{x_{B_2}}\;\Rightarrow\;x_{B_2}=\dfrac{2{,}5}{\tan 40^\circ}\approx3\;\Rightarrow\;B_2(3|0)$
Damit kann dann die Raute $A B_{2} C D_{2}$ für $\varphi=80^\circ$ gezeichnet werden.
Eingezeichnete Raute $A B_{2} C D_{2}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für die Zeichnung braucht man die Länge der halben Diagonalen $\overline{D_2B_2}$ , die im rechten oberen Dreieck mit dem Tangens berechnet werden kann.
Mit dieser Länge kann dann die Raute $A B_{2} C D_{2}$ gezeichnet werden.
Zeigen Sie, dass für den Umfang $u$ der Rauten $A B_{n} C D_{n}$ in Abhängigkeit von $\varphi$ gilt:
$u(\varphi)=\dfrac{10}{\sin(0{,}5\varphi)}\;\mathrm{cm}$ . (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Raute
Zeige, dass für den Umfang $u$ der Rauten $A B_{n} C D_{n}$ in Abhängigkeit von $\varphi$ gilt: $u(\varphi)=\dfrac{10}{\sin(0{,}5\varphi)}\;\mathrm{cm}$
Der Umfang der Raute ist:
$u=4\cdot |\overline{AB_n}|$
Berechnung von $|\overline{AB_n}|$ mithilfe des Sinus
Im unteren rechtwinkligen Dreieck $O A B_{2}$ gilt:
$\sin(0{,}5\varphi)=\dfrac{0{,}5\cdot|\overline{AC}|}{|\overline{AB_n}|}=\dfrac{2{,}5\;\mathrm{cm}}{|\overline{AB_n}|}\;$
$\Rightarrow\;|\overline{AB_n}|(\varphi)=\dfrac{2{,}5}{\sin(0{,}5\varphi)}\;\mathrm{cm}$ für $\varphi \in\;]0^\circ;180^\circ[$
Damit erhält man für $u$ :
$u=4\cdot |\overline{AB_n}|=4\cdot\dfrac{2{,}5}{\sin(0{,}5\varphi)}=\dfrac{10}{\sin(0{,}5\varphi)}\;\mathrm{cm}$
Damit ist gezeigt, dass für den Umfang $u$ der Rauten $A B_{n} C D_{n}$ in Abhängigkeit von $\varphi$ gilt: $u(\varphi)=\dfrac{10}{\sin(0{,}5\varphi)}\;\mathrm{cm}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Umfang der Raute ist $u=4\cdot |\overline{AB_n}|$ .
Berechne im unteren rechtwinkligen Dreieck $|\overline{AB_n}|$ mithilfe des Sinus.

Der Umfang der Raute $A B_{3} C D_{3}$ ist um $15 %$ kleiner als der Umfang der Raute $A B_{1} C D_{1}$ .

Berechnen Sie das zugehörige Maß $\varphi$ des Winkels $C B_{3} A$ .

Runden Sie auf zwei Stellen nach dem Komma. (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozent- und Zinsrechnung

Berechne den Umfang der Raute $A B_{1} C D_{1}$ für $\varphi=110^\circ$ .

$u(110^\circ)=\dfrac{10}{\sin(0{,}5\cdot110^\circ)}\approx12{,}21\;\mathrm{cm}$

Berechne das zugehörige Maß $\varphi$ des Winkels $C B_{3} A$

Der Umfang der Raute $A B_{3} C D_{3}$ ist um $15 %$ kleiner als der Umfang der Raute $A B_{1} C D_{1}$ , d.h. der Umgang der Raute $A B_{1} C D_{1}$ muss mit $0,85$ multipliziert werden, um den Umfang der Raute $A B_{3} C D_{3}$ zu erhalten.

$\Rightarrow\;0{,}85\cdot12{,}21=\dfrac{10}{\sin(0{,}5\varphi)}$ mit $\varphi \in\;]0^\circ;180^\circ[$

Löse die Gleichung nach $\varphi$ auf:

$\displaystyle 0{,}85\cdot12{,}21$	$=$	$\displaystyle \dfrac{10}{\sin(0{,}5\varphi)}$	$\displaystyle \cdot \sin(0{,}5\varphi)$
	↓	Löse nach $\varphi$ auf.
$\displaystyle 0{,}85\cdot12{,}21\cdot\sin(0{,}5\varphi)$	$=$	$\displaystyle 10$	$\displaystyle :(0{,}85\cdot12{,}21)$
$\displaystyle \sin(0{,}5\varphi)$	$=$	$\displaystyle \dfrac{10}{0{,}85\cdot12{,}21}$	$\displaystyle \sin^{-1}()$
$\displaystyle 0{,}5\varphi$	$=$	$\displaystyle \sin^{-1}\left(\dfrac{10}{0{,}85\cdot12{,}21}\right)$
$\displaystyle 0{,}5\varphi$	$\approx ≈$	$\displaystyle 74{,}48^\circ$	$\displaystyle \cdot 2$
$\displaystyle \varphi$	$\approx ≈$	$\displaystyle 148{,}96^\circ$

\displaystyle L=\{148{,}96^\circ\}

Das zugehörige Maß $\varphi$ des Winkels $C B_{3} A$ beträgt rund $148{,}96^\circ$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Aufgabe B 1

Berechnung der Länge der halben Diagonalen D2B2‾\overline{D_2B_2}D2​B2​​,

Hast du eine Frage oder Feedback?

Zeige, dass für den Umfang uuu der Rauten ABnCDnAB_nCD_nABn​CDn​ in Abhängigkeit von φ\varphiφ gilt: u(φ)=10sin⁡(0,5φ) cmu(\varphi)=\dfrac{10}{\sin(0{,}5\varphi)}\;\mathrm{cm}u(φ)=sin(0,5φ)10​cm

Berechnung von ∣ABn‾∣|\overline{AB_n}|∣ABn​​∣ mithilfe des Sinus

Hast du eine Frage oder Feedback?

Berechne den Umfang der Raute AB1CD1AB_1CD_1AB1​CD1​ für φ=110∘\varphi=110^\circφ=110∘.

Berechne das zugehörige Maß φ\varphiφ des Winkels CB3ACB_3ACB3​A

Hast du eine Frage oder Feedback?

Berechnung der Länge der halben Diagonalen $\overline{D_2B_2}$ ,

Zeige, dass für den Umfang $u$ der Rauten $A B_{n} C D_{n}$ in Abhängigkeit von $\varphi$ gilt: $u(\varphi)=\dfrac{10}{\sin(0{,}5\varphi)}\;\mathrm{cm}$

Berechnung von $|\overline{AB_n}|$ mithilfe des Sinus

Berechne den Umfang der Raute $A B_{1} C D_{1}$ für $\varphi=110^\circ$ .

Berechne das zugehörige Maß $\varphi$ des Winkels $C B_{3} A$