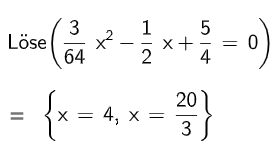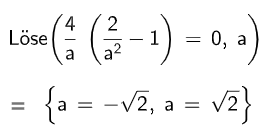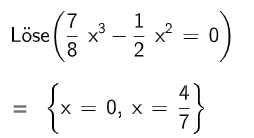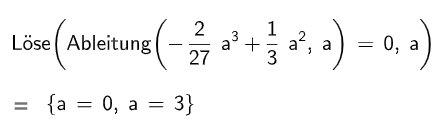Teil B: Analysis 2 - lernen mit Serlo!

Aufgabe 1

Gegeben ist die Schar der in $ℝ$ definierten Funktionen $f_{a}$ mit $f_{a} (x) = \frac{1}{a^{3}} x^{3} - \frac{1}{a} x^{2} + x$ und $a \in ℝ, a > 0$ .

Berechnen Sie die Stellen, an denen der Graph von $f_{4}$ eine Steigung von $- \frac{1}{4}$ hat. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Berechne die Stellen, an denen der Graph von $f_{4}$ eine Steigung von $- \frac{1}{4}$ hat
Gegeben ist $f_{a} (x) = \frac{1}{a^{3}} x^{3} - \frac{1}{a} x^{2} + x$ .
$\Rightarrow f_{4} (x) = \frac{1}{64} x^{3} - \frac{1}{4} x^{2} + x$
Berechne $f_{4}^{'} (x) = \frac{3}{64} x^{2} - \frac{1}{2} x + 1$
Löse die Gleichung $f_{4}^{'} (x) = - \frac{1}{4} \Rightarrow \frac{3}{64} x^{2} - \frac{1}{2} x + 1 = - \frac{1}{4}$
$\Rightarrow \frac{3}{64} x^{2} - \frac{1}{2} x + \frac{5}{4} = 0$
Die Stellen, an denen der Graph von $f_{4}$ eine Steigung von $- \frac{1}{4}$ hat, sind $x = 4$ und $x = \frac{20}{3}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Löse die Gleichung $f^{'} (x) = - \frac{1}{4} .$
Bestimmen Sie den Wert von $a$ so, dass der Punkt $(2 | 2)$ auf dem Graphen von $f_{a}$ liegt.
(3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Bestimme den Wert von $a$ so, dass der Punkt $(2 | 2)$ auf dem Graphen von $f_{a}$ liegt
Für $a > 0$ soll gelten: $f_{a} (2) = 2$ .
$f_{a} (2) = \frac{1}{a^{3}} \cdot 2^{3} - \frac{1}{a} \cdot 2^{2} + 2 = 2 \Rightarrow \frac{1}{a^{3}} \cdot 8 - \frac{1}{a} \cdot 4 = 0 \Rightarrow \frac{4}{a} \cdot (\frac{2}{a^{2}} - 1) = 0$
(Wegen $a > 0$ entfällt die Lösung $- \sqrt{a}$ .)
Der Punkt $(2 | 2)$ liegt für $a = \sqrt{2}$ auf dem Graphen von $f_{a}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Löse die Gleichung $f_{a} (2) = 2$ nach $a$ auf.
Ermitteln Sie die Koordinaten der gemeinsamen Punkte der Graphen von $f_{1}$ und $f_{2}$ .
Weisen Sie nach, dass es nur einen Punkt gibt, der auf jedem Graphen der Schar liegt.
(2 P+3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
Ermittele die Koordinaten der gemeinsamen Punkte der Graphen von $f_{1}$ und $f_{2}$
$f_{a} (x) = \frac{1}{a^{3}} x^{3} - \frac{1}{a} x^{2} + x$
$\Rightarrow f_{1} (x) = x^{3} - x^{2} + x$ und $f_{2} (x) = \frac{1}{8} x^{3} - \frac{1}{2} x^{2} + x$
Zur Berechnung der gemeinsamen Punkte der Graphen von $f_{1}$ und $f_{2}$ setze $f_{1} = f_{2}$ .
$\Rightarrow x^{3} - x^{2} + x = \frac{1}{8} x^{3} - \frac{1}{2} x^{2} + x \Rightarrow \frac{7}{8} x^{3} - \frac{1}{2} x^{2} = 0$
Berechne die zu $x = 0$ und $x = \frac{4}{7}$ gehörenden Funktionswerte:
$f_{1} (0) = 0$ und $f_{1} (\frac{4}{7}) = \frac{148}{343}$
Die Punkte $(0 | 0)$ und $(\frac{4}{7} | \frac{148}{343}) \approx (0,57 | 0,43)$ sind die gemeinsamen Punkte der Graphen von $f_{1}$ und $f_{2}$ .
Weise nach, dass es nur einen Punkt gibt, der auf jedem Graphen der Schar liegt
$f_{a} (0) = 0$ gilt unabhängig von $a$ . Wegen $f_{3} (\frac{4}{7}) \approx 0,47 \neq f_{1} (\frac{4}{7}) \approx 0,43$ liegt ausschließlich der Koordinatenursprung auf allen Graphen der Schar.

Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Zur Berechnung der gemeinsamen Punkte der Graphen von $f_{1}$ und $f_{2}$ setze $f_{1} = f_{2}$ .
Vereinfache die Gleichung und löse sie nach $x$ auf. Es gibt zwei Lösungen.
Berechne die zugehörigen Funktionswerte.
Teil 2
$f_{a} (0) = 0$ gilt unabhängig von $a$ .
Vergleiche z.B. $f_{3} (\frac{4}{7})$ mit $f_{1} (\frac{4}{7})$ . Was folgt daraus?
Die Gleichung $f_{a} (x) = 0$ hat in Abhängigkeit von $a$ die Lösungen
0 und $\frac{a^{2} + \sqrt{a^{3} (a - 4)}}{2}$ und $\frac{a^{2} - \sqrt{a^{3} (a - 4)}}{2}$ , wobei die Lösung $0$ nicht mit den anderen beiden Lösungen zusammenfallen kann.
Geben Sie die Anzahl der Nullstellen von $f_{a}$ in Abhängigkeit von $a$ an und begründen Sie Ihre Angabe anhand der obigen Terme. (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
Gib die Anzahl der Nullstellen von $f_{a}$ in Abhängigkeit von $a$ an und begründe Deine Angabe anhand der obigen Terme
Gegeben sind:
0; $\frac{a^{2} + \sqrt{a^{3} (a - 4)}}{2}$ ; $\frac{a^{2} - \sqrt{a^{3} (a - 4)}}{2}$
Für $a > 0$ ist auch $a^{3} > 0$ .
Betrachte den Term $(a - 4)$ :
Wenn $a - 4 < 0$ ist, folgt $0 < a < 4$ und die beiden Terme mit den Wurzeln entfallen als Nullstellen. Es gibt also nur $1$ Nullstelle $x = 0$ .
Wenn $a - 4 = 0$ ist, folgt $a = 4$ und die beiden Terme mit den Wurzeln fallen zusammen. Es gibt $2$ Nullstellen $x = 0$ und $x = \frac{a^{2}}{2}$ .
Wenn $a - 4 > 0$ ist, folgt $a > 4$ und es gibt die $3$ oben angegebenen Nullstellen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für $a > 0$ ist auch $a^{3} > 0$ .
Betrachte den Term $(a - 4)$ und führe eine Fallunterscheidung durch.
Der Graph jeder Funktion $f_{a}$ hat genau einen Wendepunkt.
Bestimmen Sie den Wert von $a$ zu dem Wendepunkt mit der größten y-Koordinate. (5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
Bestimme den Wert von $a$ zu dem Wendepunkt mit der größten y-Koordinate
Bekannt ist, dass der Graph jeder Funktion $f_{a}$ genau einen Wendepunkt hat.
Berechne $f_{a}^{''} (x) = 0$ .
$f^{'} (x) = 3 \cdot \frac{x^{2}}{a^{3}} - 2 \cdot \frac{x}{a} + 1$
Dann ist $f^{''} (x) = (f^{'} (x))^{'}$ .
Berechnung der zweiten Ableitung und Lösung von $f_{a}^{''} (x) = 0$
Die einzige Wendestelle liegt also bei $x = \frac{a^{2}}{3}$ .
Wendepunkt mit der größten y-Koordinate
Berechne die $y$ -Koordinate $f_{a} (\frac{a^{2}}{3})$ des Wendepunktes.
$f_{a} (\frac{a^{2}}{3}) = - \frac{2}{27} a^{3} + \frac{1}{3} a^{2} = f (a)$
Für die Berechnung der maximalen y-Koordinate löse $f^{'} (a) = 0$ .
Wegen $a > 0$ ist $a = 3$ die gesuchte Lösung.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $f_{a}^{''} (x) = 0$ . $\Rightarrow$ Man erhält eine Lösung $x_{1}$ in Abhängigkeit von $a$ .
Berechne $f_{a} (x_{1})$ und löse $f_{a}^{'} (x_{1}) = 0 \Rightarrow$ liefert wegen $a > 0$ nur eine Lösung.
Im Folgenden gilt $a = 4$ .
Abbildung 1 zeigt beispielhaft den Graphen einer Funktion $f_{a}$ sowie die Gerade $g$ mit der Gleichung $y = x$ , die den Graphen in den Punkten $O (0 | 0)$ und $P (u_{a} | f_{a} (u_{a}))$ schneidet. Die Gerade $g$ , die $x$ -Achse und die Gerade mit der Gleichung $x = u_{a}$ begrenzen ein rechtwinkliges Dreieck.
Abbildung 1
Die folgenden Schritte stellen die Lösung einer Aufgabe dar:
- $f_{a} (x) = x \Leftrightarrow x = 0 \lor x = a^{2}$ .
- $\frac{1}{2} \cdot a^{2} \cdot f_{a} (a^{2}) = 3 \cdot \int_{0}^{a^{2}} (x - f_{a} (x)) d x \Leftrightarrow a = 2$ .
Erläutern Sie diese Schritte und interpretieren Sie die Lösung $a = 2$ geometrisch. (5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Erläutere diese Schritte und interpretiere die Lösung $a = 2$ geometrisch
1. Rechenschritt: Zunächst werden die Schnittstellen der Gerade $g$ mit dem Graphen von $f_{a}$ berechnet $\Rightarrow f_{a} (x) = x \Leftrightarrow x = 0 \lor x = a^{2}$
2. Rechenschritt:
Die Lösung $a = 2$ der Gleichung $\frac{1}{2} \cdot a^{2} \cdot f_{a} (a^{2}) = 3 \cdot \int_{0}^{a^{2}} (x - f_{a} (x)) d x$ gibt denjenigen Wert von $a$ an, für den das rechtwinklige Dreieck den dreifachen Flächeninhalt besitzt wie das Flächenstück, das von $g$ und dem Graphen von $f_{a}$ eingeschlossen ist.
Die folgende Abbildung ist nicht im Aufgabentext gefordert. Sie dient nur zur Veranschaulichung.
Für $a = 2$ ist der Flächeninhalt des Dreiecks $A_{△} = 8 FE$ und der Flächeninhalt zwischen der Geraden $g$ mit dem Graphen von $f_{2}$ beträgt $A = \frac{8}{3} FE$ , sodass $A_{△} = 3 \cdot A$ ist $\Rightarrow 8 = 3 \cdot \frac{8}{3} ✓$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Im ersten Rechenschritt werden die Schnittstellen der Gerade $g$ mit dem Graphen von $f_{a}$ berechnet.
Im zweiten Rechenschritt steht auf der linken Gleichungsseite der Flächeninhalt eines rechtwinkligen Dreiecks und auf der rechten Gleichungsseite steht der dreifache Flächeninhalt des Flächenstücks, das von $g$ und dem Graphen von $f_{a}$ eingeschlossen ist.
Die Lösung dieser Gleichung ist $a = 2$ .
Abbildung 2 zeigt den Graphen der Funktion $f_{4}$ .
Abbildung 2
$h$ ist die Funktion, deren Graph durch Spiegelung des Graphen von $f_{4}$ an der $x$ -Achse entsteht.
(i) Skizzieren Sie in Abbildung 2 den Graphen von $h$ sowie die Fläche $A$ , die von $x = 0$ bis $x = 12$ zwischen den Graphen von $f_{4}$ und $h$ liegt. (2 P)
(ii) Berechnen Sie den Inhalt der Fläche $A$ . (3 P)
(iii) Es gibt einen Wert von $c \in ℝ, c > 0$ , für den die Fläche, die im Bereich von $x = c$ bis $x = 8$ zwischen dem Graphen von $f_{4}$ und der $x$ -Achse liegt, den Flächeninhalt $\frac{5}{3} FE$ besitzt.
Geben Sie eine Gleichung an, mit der man diesen Wert von $c$ ermitteln kann. (1 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
(i) Skizziere in Abbildung 2 den Graphen von $h$ sowie die Fläche $A$ , die von $x = 0$ bis $x = 12$ zwischen den Graphen von $f_{4}$ und $h$ liegt
Abbildung 2 mit Graph h und der eingeschlossenen Fläche
Der Graph von $h$ wurde durch Spiegelung des Graphen von $f_{4}$ an der $x$ -Achse erzeugt.
(ii) Berechne den Inhalt der Fläche $A$
$f_{4} (x) = \frac{1}{64} x^{3} - \frac{1}{4} x^{2} + x$
Der Flächeninhalt wird berechnet mit:
$A = 2 \cdot \int_{0}^{12} f_{4} (x) d x = 18$
Der Inhalt der eingeschlossenen Fläche beträgt $18 FE$ .
(iii) Gib eine Gleichung an, mit der man diesen Wert von $c$ ermitteln kann
Gegeben: Die Fläche, die im Bereich von $x = c$ bis $x = 8$ zwischen dem Graphen von $f_{4}$ und der $x$ -Achse liegt, hat den Flächeninhalt $\frac{5}{3} FE$ .
Die zugehörige Gleichung lautet also:

$\int_{c}^{8} f_{4} (x) d x = \frac{5}{3}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil (i)
Der Graph von $h$ wird durch Spiegelung des Graphen von $f_{4}$ an der $x$ -Achse erzeugt.
Teil (ii)
Der Flächeninhalt wird berechnet mit $A = 2 \cdot \int_{0}^{12} f_{4} (x) d x$
Teil (iii)
Gegeben ist $A = \frac{5}{3}$ . Die Fläche berechnet sich mit $A = \int_{c}^{8} f_{4} (x) d x$ .
Erstelle eine Gleichung.

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

Aufgabe 1

Berechne die Stellen, an denen der Graph von f4 eine Steigung von −14 hat

Hast du eine Frage oder Feedback?

Bestimme den Wert von a so, dass der Punkt (2|2) auf dem Graphen von fa liegt

Hast du eine Frage oder Feedback?

Ermittele die Koordinaten der gemeinsamen Punkte der Graphen von f1 und f2

Weise nach, dass es nur einen Punkt gibt, der auf jedem Graphen der Schar liegt

Hast du eine Frage oder Feedback?

Gib die Anzahl der Nullstellen von fa in Abhängigkeit von a an und begründe Deine Angabe anhand der obigen Terme

Hast du eine Frage oder Feedback?

Bestimme den Wert von a zu dem Wendepunkt mit der größten y-Koordinate

Wendepunkt mit der größten y-Koordinate

Hast du eine Frage oder Feedback?

Erläutere diese Schritte und interpretiere die Lösung a=2 geometrisch

Hast du eine Frage oder Feedback?

(i) Skizziere in Abbildung 2 den Graphen von h sowie die Fläche A, die von x=0 bis x=12 zwischen den Graphen von f4 und h liegt

Abbildung 2 mit Graph h und der eingeschlossenen Fläche

(ii) Berechne den Inhalt der Fläche A

(iii) Gib eine Gleichung an, mit der man diesen Wert von c ermitteln kann

Hast du eine Frage oder Feedback?

Berechne die Stellen, an denen der Graph von $f_{4}$ eine Steigung von $- \frac{1}{4}$ hat

Bestimme den Wert von $a$ so, dass der Punkt $(2 | 2)$ auf dem Graphen von $f_{a}$ liegt

Ermittele die Koordinaten der gemeinsamen Punkte der Graphen von $f_{1}$ und $f_{2}$

Gib die Anzahl der Nullstellen von $f_{a}$ in Abhängigkeit von $a$ an und begründe Deine Angabe anhand der obigen Terme

Bestimme den Wert von $a$ zu dem Wendepunkt mit der größten y-Koordinate

Erläutere diese Schritte und interpretiere die Lösung $a = 2$ geometrisch

(i) Skizziere in Abbildung 2 den Graphen von $h$ sowie die Fläche $A$ , die von $x = 0$ bis $x = 12$ zwischen den Graphen von $f_{4}$ und $h$ liegt

(ii) Berechne den Inhalt der Fläche $A$

(iii) Gib eine Gleichung an, mit der man diesen Wert von $c$ ermitteln kann