Teil B-Aufgabengruppe I - lernen mit Serlo!

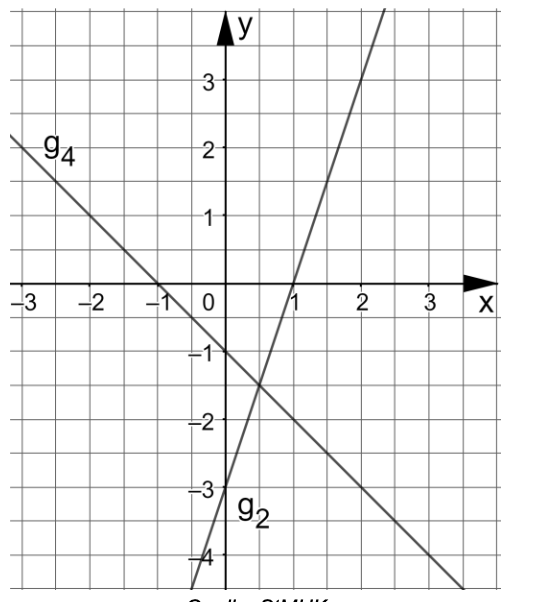
Die Gerade $g_{1}$ verläuft durch die Punkte $A (1 ∣ - 3)$ und $B (3 ∣ - 5)$ .
Ermitteln Sie rechnerisch die Funktionsgleichung der Geraden $g_{1}$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Ermitteln der Funktionsgleichung der Geraden $\mathrm{g_1}$
Die allgemeine Geradengleichung lautet:
$\mathrm{y=m\cdot x+t}$
Berechnen der Steigung $m$ .
$\displaystyle\mathrm{m=\frac{y_2-y_1}{x_2-x_1}\ \Rightarrow\ m=\frac{-5-(-3)}{3-1}=\frac{-2}{2}}$
$\mathrm{m=-1}$
Einsetzen von $m$ und der Koordinaten, z.B. des Punktes $\text{A}$ , in die allgemeine Geradengleichung.
$\mathrm{-3=-1\cdot 1+t\ \Rightarrow\ t=-3+1}$
$\mathrm{t=-2}$
Die Funktionsgleichung der Geraden $g_{1}$ lautet:
$\boxed{\mathrm{g_1:\ y=-x-2}}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne die Steigung $m .$
Berechne den $\text{y}$ -Achsenabschnitt $\text{t}$ .
Stelle die Funktionsgleichung der Geraden $\mathrm{g_1}$ auf.
Gegeben ist die Gerade $g_{2} : y = 3 x - 3$ .
Überprüfen Sie rechnerisch, ob der Punkt $C (1,5 ∣ 1,5)$ auf dieser Geraden
liegt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Überprüfen, ob der Punkt $\text{C}$ auf $\mathrm{g_2}$ liegt.
Einsetzen der Koordinaten des Punktes $\text{C}$ in die Geradengleichung:
$\mathrm{g_2:y=3x-3}$
$\mathrm{y=3\cdot 1{,}5-3}$
$\text{y}=4{,}5-3$
$\mathrm{y=1{,}5\Rightarrow\ C}$ liegt auf der Geraden $\mathrm{g_2}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Setzte die Koordinaten des Punkts C in die Funktionsgleichung von $\mathrm{g_2}$ ein.
Die Gerade $g_{3}$ verläuft durch den Punkt $D (3 ∣ - 2)$ und steht senkrecht auf der
Geraden $g_{2} .$
Ermitteln Sie die Funktionsgleichung der Geraden $g_{3}$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Ermitteln Sie die Funktionsgleichung der Geraden $g_{3}$ .
Da $\mathrm{g_3}$ senkrecht auf $\mathrm{g_2}$ steht, gilt für die Steigung $\mathrm{m_3}$ der Geraden $\mathrm{g_3}$ :
$\mathrm{m_2\cdot m_3}=-1$
$\mathrm{m_2=3}$
ermitteln von $\mathrm{m_3}$
$\mathrm{3\cdot m_3=-1\ \Rightarrow\ m_3=-\dfrac{1}{3}}$
Einsetzen der Koordinaten des Punktes $\text{C}$ in die allgemeine Geradengleichung:
$\mathrm{-2=-\dfrac{1}{3}\cdot 3+t_3}$
$\mathrm{t_3=-2+1\ \Rightarrow\ t_3=-1}$
Die Geradengleichung der Geraden $\mathrm{g_3}$ lautet dann:
$\boxed{\mathrm{g_3:y=-\dfrac{1}{3}x-1}}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme die Steigung $m$ .
Ermittle den $\text{y}$ Achsenabschnitt.
Stelle die Funktionsgleichung auf.
Berechnen Sie die $x$ -Koordinate des Schnittpunkts $N_{4}$ der
Geraden $g_{4} : y = - x - 1$ mit der $x$ -Achse.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungen
Berechnen der $\text{x}$ -Koordinate des Schnittpunkts $\mathrm{N_4}$ .
$\mathrm{g_4:y=-x-1}$

setze $\mathrm{y=0}$
$\mathrm{0=-x-1}$
$\mathrm{x=-1}$
Die $\text{x}$ -Koordinate des Schnittpunkts $\mathrm{N_4}$ ist dann:
$\boxed{\mathrm{x=-1}}$

Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Setze $\mathrm{y=0}$ und berechne $\text{x}$ .

Ermitteln Sie rechnerisch die Koordinaten des Schnittpunkts $S$ der Geraden $g_{2}$ und g $_{4}$ und geben Sie $S$ an.

Die Geraden $g_5:y=\frac{3}{7}x-3\$ und $g_6:y=\frac{3}{7}x-7\ \$ haben keinen gemeinsamen Punkt.
Verändern Sie genau eine Zahl in einer der beiden Funktionsgleichungen so,
dass die beiden Geraden mindestens einen Punkt gemeinsam haben.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Verändern einer Zahl in einer der beiden Funktionsgleichungen so, dass die beiden Geraden mindestens einen Punkt gemeinsam haben.
$\mathrm{g_5:y=\frac{3}{7}x-3}$
$\mathrm{g_6:y=\frac{3}{7}x-7}$
Ändern der Steigung der Geraden $\mathrm{g_6}$ :
z. B.
$\mathrm{g_6:y=4x-7}$
Hinweis:
Du kannst auch die $\text{y}$ -Achsenabschnitte gleichsetzen, so dass gilt: $\mathrm{t_5=t_6}$ .
Die Geraden liegen dann aufeinander und haben unendlich viele Punkte gemeinsam.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Geraden $\mathrm{g_5}$ und $\mathrm{g_6}$ sind parallel, da $\mathrm{m_5=m_6}$ und $\mathrm{t_5\neq t_6}.$
Verändere die Steigung $\text{m}$ einer der Geradengleichungen.
Zeichnen Sie die Geraden $\mathrm{g_2}$ und $\mathrm{g}_4$ in ein Koordinatensystem mit der
Längeneinheit $1\cm$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Einzeichnen der Geraden $\mathrm{g_2}$ und $\mathrm{g_4}$ in ein Koordinatensystem.
Die Zeichnung ist nicht maßtreu.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Gleichsetzen der Geradengleichungen
	↓
$\displaystyle \mathrm{3x-3}$	$=$	$\displaystyle \mathrm{-x-1}$	$\displaystyle +\text{x}$
	↓	addieren
$\displaystyle \mathrm{4x-3}$	$=$	$\displaystyle -1$	$\displaystyle +3$
	↓	subtrahieren
$\displaystyle \mathrm{4x}$	$=$	$\displaystyle 2$	$\displaystyle :4$
	↓	dividieren
$\displaystyle \text{x}$	$=$	$\displaystyle 0{,}5$

Ermitteln der Funktionsgleichung der Geraden $\mathrm{g_1}$

Hast du eine Frage oder Feedback?

Überprüfen, ob der Punkt $\text{C}$ auf $\mathrm{g_2}$ liegt.

Hast du eine Frage oder Feedback?

Ermitteln Sie die Funktionsgleichung der Geraden $g_{3}$ .

Hast du eine Frage oder Feedback?

Berechnen der $\text{x}$ -Koordinate des Schnittpunkts $\mathrm{N_4}$ .

Hast du eine Frage oder Feedback?

Ermitteln der Koordinaten des Schnittpunkts $\text{S}$ der Geraden $\mathrm{g_2}$ und $\mathrm{g_4}$ .

Hast du eine Frage oder Feedback?

Verändern einer Zahl in einer der beiden Funktionsgleichungen so, dass die beiden Geraden mindestens einen Punkt gemeinsam haben.

Hinweis:

Hast du eine Frage oder Feedback?

Einzeichnen der Geraden $\mathrm{g_2}$ und $\mathrm{g_4}$ in ein Koordinatensystem.

Hast du eine Frage oder Feedback?

Ermitteln der Funktionsgleichung der Geraden g1\mathrm{g_1}g1​

Hast du eine Frage oder Feedback?

Überprüfen, ob der Punkt C\text{C}C auf g2\mathrm{g_2}g2​ liegt.

Hast du eine Frage oder Feedback?

Ermitteln Sie die Funktionsgleichung der Geraden g3g_3g3​.

Hast du eine Frage oder Feedback?

Berechnen der x\text{x}x-Koordinate des Schnittpunkts N4\mathrm{N_4}N4​.

Hast du eine Frage oder Feedback?

Ermitteln der Koordinaten des Schnittpunkts S\text{S}S der Geraden g2\mathrm{g_2}g2​ und g4\mathrm{g_4}g4​.

Hast du eine Frage oder Feedback?

Verändern einer Zahl in einer der beiden Funktionsgleichungen so, dass die beiden Geraden mindestens einen Punkt gemeinsam haben.

Hinweis:

Hast du eine Frage oder Feedback?

Einzeichnen der Geraden g2\mathrm{g_2}g2​ und g4\mathrm{g_4}g4​ in ein Koordinatensystem.

Hast du eine Frage oder Feedback?

Ermitteln der Funktionsgleichung der Geraden $\mathrm{g_1}$

Überprüfen, ob der Punkt $\text{C}$ auf $\mathrm{g_2}$ liegt.

Ermitteln Sie die Funktionsgleichung der Geraden $g_{3}$ .

Berechnen der $\text{x}$ -Koordinate des Schnittpunkts $\mathrm{N_4}$ .

Ermitteln der Koordinaten des Schnittpunkts $\text{S}$ der Geraden $\mathrm{g_2}$ und $\mathrm{g_4}$ .

Einzeichnen der Geraden $\mathrm{g_2}$ und $\mathrm{g_4}$ in ein Koordinatensystem.