Teil B-Aufgabengruppe I

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

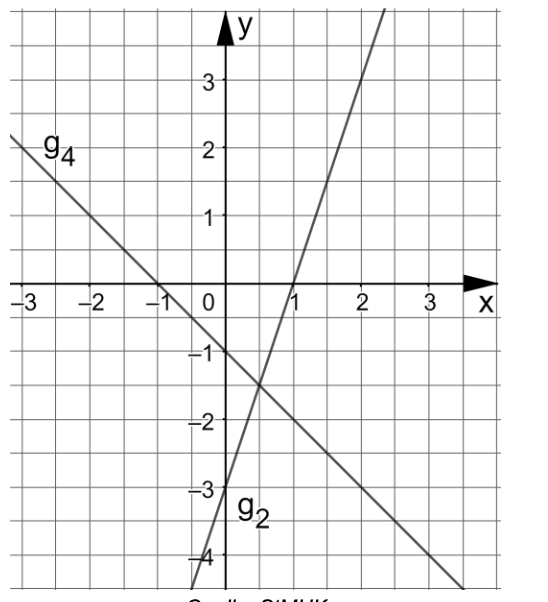
Die Gerade $g_{1}$ verläuft durch die Punkte $A (1 ∣ - 3)$ und $B (3 ∣ - 5)$ .
Ermitteln Sie rechnerisch die Funktionsgleichung der Geraden $g_{1}$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Ermitteln der Funktionsgleichung der Geraden $\mathrm{g_1}$
Die allgemeine Geradengleichung lautet:
$\mathrm{y=m\cdot x+t}$
Berechnen der Steigung $m$ .
$\displaystyle\mathrm{m=\frac{y_2-y_1}{x_2-x_1}\ \Rightarrow\ m=\frac{-5-(-3)}{3-1}=\frac{-2}{2}}$
$\mathrm{m=-1}$
Einsetzen von $m$ und der Koordinaten, z.B. des Punktes $\text{A}$ , in die allgemeine Geradengleichung.
$\mathrm{-3=-1\cdot 1+t\ \Rightarrow\ t=-3+1}$
$\mathrm{t=-2}$
Die Funktionsgleichung der Geraden $g_{1}$ lautet:
$\boxed{\mathrm{g_1:\ y=-x-2}}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Steigung $m .$
Berechne den $\text{y}$ -Achsenabschnitt $\text{t}$ .
Stelle die Funktionsgleichung der Geraden $\mathrm{g_1}$ auf.
Gegeben ist die Gerade $g_{2} : y = 3 x - 3$ .
Überprüfen Sie rechnerisch, ob der Punkt $C (1,5 ∣ 1,5)$ auf dieser Geraden
liegt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Überprüfen, ob der Punkt $\text{C}$ auf $\mathrm{g_2}$ liegt.
Einsetzen der Koordinaten des Punktes $\text{C}$ in die Geradengleichung:
$\mathrm{g_2:y=3x-3}$
$\mathrm{y=3\cdot 1{,}5-3}$
$\text{y}=4{,}5-3$
$\mathrm{y=1{,}5\Rightarrow\ C}$ liegt auf der Geraden $\mathrm{g_2}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Setzte die Koordinaten des Punkts C in die Funktionsgleichung von $\mathrm{g_2}$ ein.
Die Gerade $g_{3}$ verläuft durch den Punkt $D (3 ∣ - 2)$ und steht senkrecht auf der
Geraden $g_{2} .$
Ermitteln Sie die Funktionsgleichung der Geraden $g_{3}$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Ermitteln Sie die Funktionsgleichung der Geraden $g_{3}$ .
Da $\mathrm{g_3}$ senkrecht auf $\mathrm{g_2}$ steht, gilt für die Steigung $\mathrm{m_3}$ der Geraden $\mathrm{g_3}$ :
$\mathrm{m_2\cdot m_3}=-1$
$\mathrm{m_2=3}$
ermitteln von $\mathrm{m_3}$
$\mathrm{3\cdot m_3=-1\ \Rightarrow\ m_3=-\dfrac{1}{3}}$
Einsetzen der Koordinaten des Punktes $\text{C}$ in die allgemeine Geradengleichung:
$\mathrm{-2=-\dfrac{1}{3}\cdot 3+t_3}$
$\mathrm{t_3=-2+1\ \Rightarrow\ t_3=-1}$
Die Geradengleichung der Geraden $\mathrm{g_3}$ lautet dann:
$\boxed{\mathrm{g_3:y=-\dfrac{1}{3}x-1}}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme die Steigung $m$ .
Ermittle den $\text{y}$ Achsenabschnitt.
Stelle die Funktionsgleichung auf.
Berechnen Sie die $x$ -Koordinate des Schnittpunkts $N_{4}$ der
Geraden $g_{4} : y = - x - 1$ mit der $x$ -Achse.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungen
Berechnen der $\text{x}$ -Koordinate des Schnittpunkts $\mathrm{N_4}$ .
$\mathrm{g_4:y=-x-1}$

setze $\mathrm{y=0}$
$\mathrm{0=-x-1}$
$\mathrm{x=-1}$
Die $\text{x}$ -Koordinate des Schnittpunkts $\mathrm{N_4}$ ist dann:
$\boxed{\mathrm{x=-1}}$

Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Setze $\mathrm{y=0}$ und berechne $\text{x}$ .

Ermitteln Sie rechnerisch die Koordinaten des Schnittpunkts $S$ der Geraden $g_{2}$ und g $_{4}$ und geben Sie $S$ an.

Die Geraden $g_5:y=\frac{3}{7}x-3\$ und $g_6:y=\frac{3}{7}x-7\ \$ haben keinen gemeinsamen Punkt.
Verändern Sie genau eine Zahl in einer der beiden Funktionsgleichungen so,
dass die beiden Geraden mindestens einen Punkt gemeinsam haben.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Verändern einer Zahl in einer der beiden Funktionsgleichungen so, dass die beiden Geraden mindestens einen Punkt gemeinsam haben.
$\mathrm{g_5:y=\frac{3}{7}x-3}$
$\mathrm{g_6:y=\frac{3}{7}x-7}$
Ändern der Steigung der Geraden $\mathrm{g_6}$ :
z. B.
$\mathrm{g_6:y=4x-7}$
Hinweis:
Du kannst auch die $\text{y}$ -Achsenabschnitte gleichsetzen, so dass gilt: $\mathrm{t_5=t_6}$ .
Die Geraden liegen dann aufeinander und haben unendlich viele Punkte gemeinsam.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die Geraden $\mathrm{g_5}$ und $\mathrm{g_6}$ sind parallel, da $\mathrm{m_5=m_6}$ und $\mathrm{t_5\neq t_6}.$
Verändere die Steigung $\text{m}$ einer der Geradengleichungen.
Zeichnen Sie die Geraden $\mathrm{g_2}$ und $\mathrm{g}_4$ in ein Koordinatensystem mit der
Längeneinheit $1\cm$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Einzeichnen der Geraden $\mathrm{g_2}$ und $\mathrm{g_4}$ in ein Koordinatensystem.
Die Zeichnung ist nicht maßtreu.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
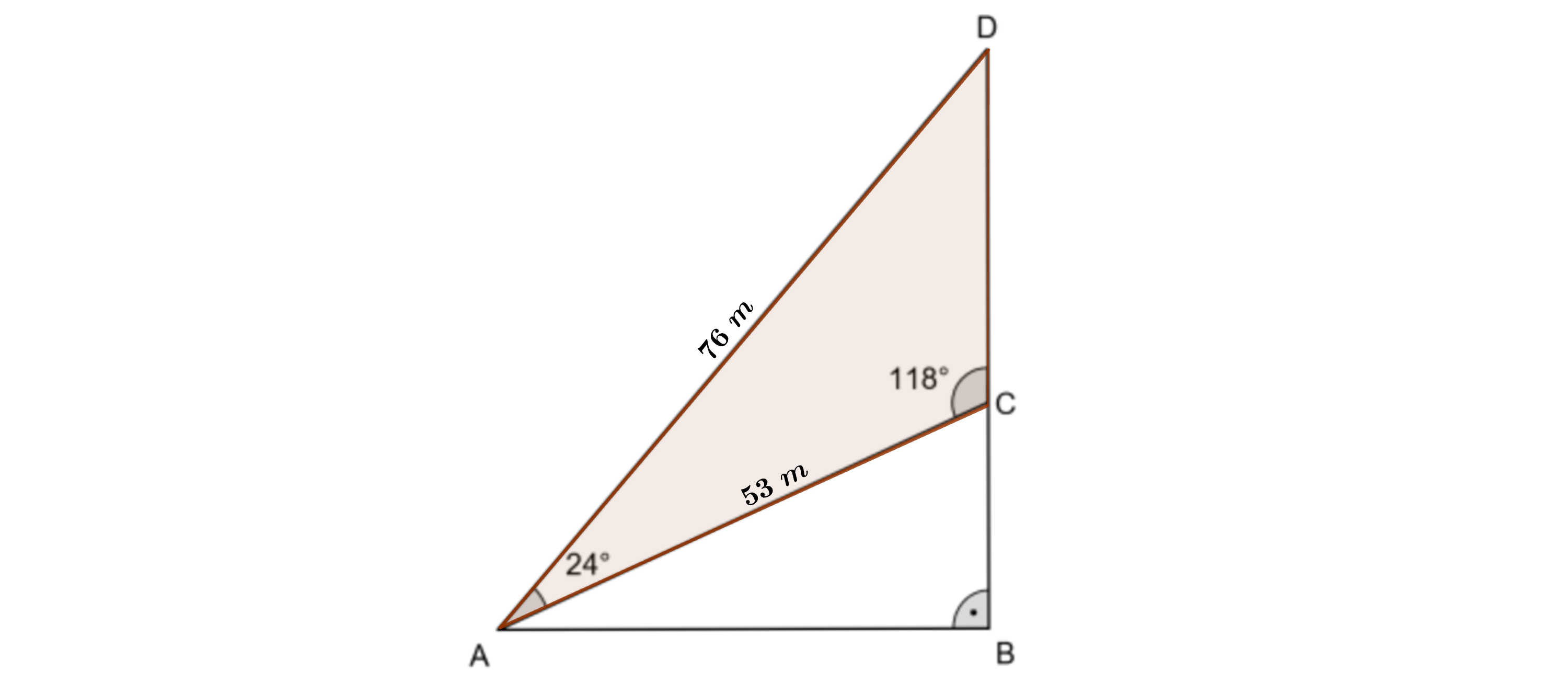
In der folgenden Skizze gilt: $\mathrm{|\overline{AC}|=53\m}$
1. Berechnen Sie den Flächeninhalt des Dreiecks $\text{ACD}$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreiecksfläche berechnen
  Berechnen des Flächeninhalts des Dreiecks $\text{ACD}$ .
  Zur Berechnung des Flächeninhalts des Dreiecks $\text{ABD}$ verwenden wir die Formel:
  $\boxed{\mathrm{A_{ACD}=\dfrac{1}{2}\cdot \overline{AD}\cdot \overline{AC}\cdot sin\sphericalangle{DAC}}}$
  Wir berechnen zuerst $\mathrm{\overline{AD}}$ mit dem Sinussatz.
  Der Sinussatz, angewendet auf unser Dreieck, lautet:
  $\mathrm{\dfrac{\overline{AD}}{\sin118^\circ}=\dfrac{53}{\sin\sphericalangle{CDA}}}$
  Berechnen von $\mathrm{\sphericalangle{CDA}}$ .
  $\mathrm{\sphericalangle{CDA}=180^\circ-118^\circ-24^\circ}$
  $\mathrm{\sphericalangle{CDA}=38^\circ}$
  Einsetzen der Werte in die Formel:
  $\mathrm{\dfrac{\overline{AD}}{\sin118^\circ}=\dfrac{53}{\sin38^\circ}\Rightarrow\ \overline{AD}=\dfrac{53\cdot \sin118^\circ}{\sin38^\circ}}$
  $\mathrm{\overline{AD}=76{,}00\m}$
  Berechnen des Flächeninhalts des Dreiecks $\text{ACD}$ .
  $\mathrm{A_{ACD}=\dfrac{1}{2}\cdot 76\cdot 53\cdot sin24^\circ}$
  $\mathrm{A_{ACD}=2014\cdot 0{,}4067\ \ [m^2]}$
  $\mathrm{A_{ACD}\approx819{,}1\m^2}$
  Der Flächeninhalt des Dreiecks $\text{ACD}$ beträgt ungefähr: $\boxed{819\m^2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Flächeninhalt des Dreiecks $\text{ACD}$ mit der Formel: $\boxed{\mathrm{\dfrac{1}{2}\cdot \overline{AD}\cdot \overline{AC}\cdot sin\sphericalangle{DAC}}}$
  Bestimme die Strecke $\mathrm{\overline{AD}}$ mit Hilfe des Sinussatzes.
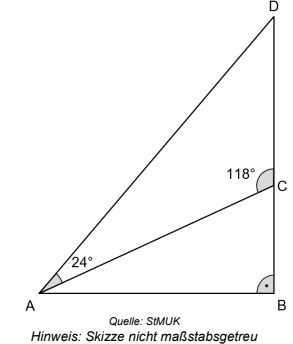
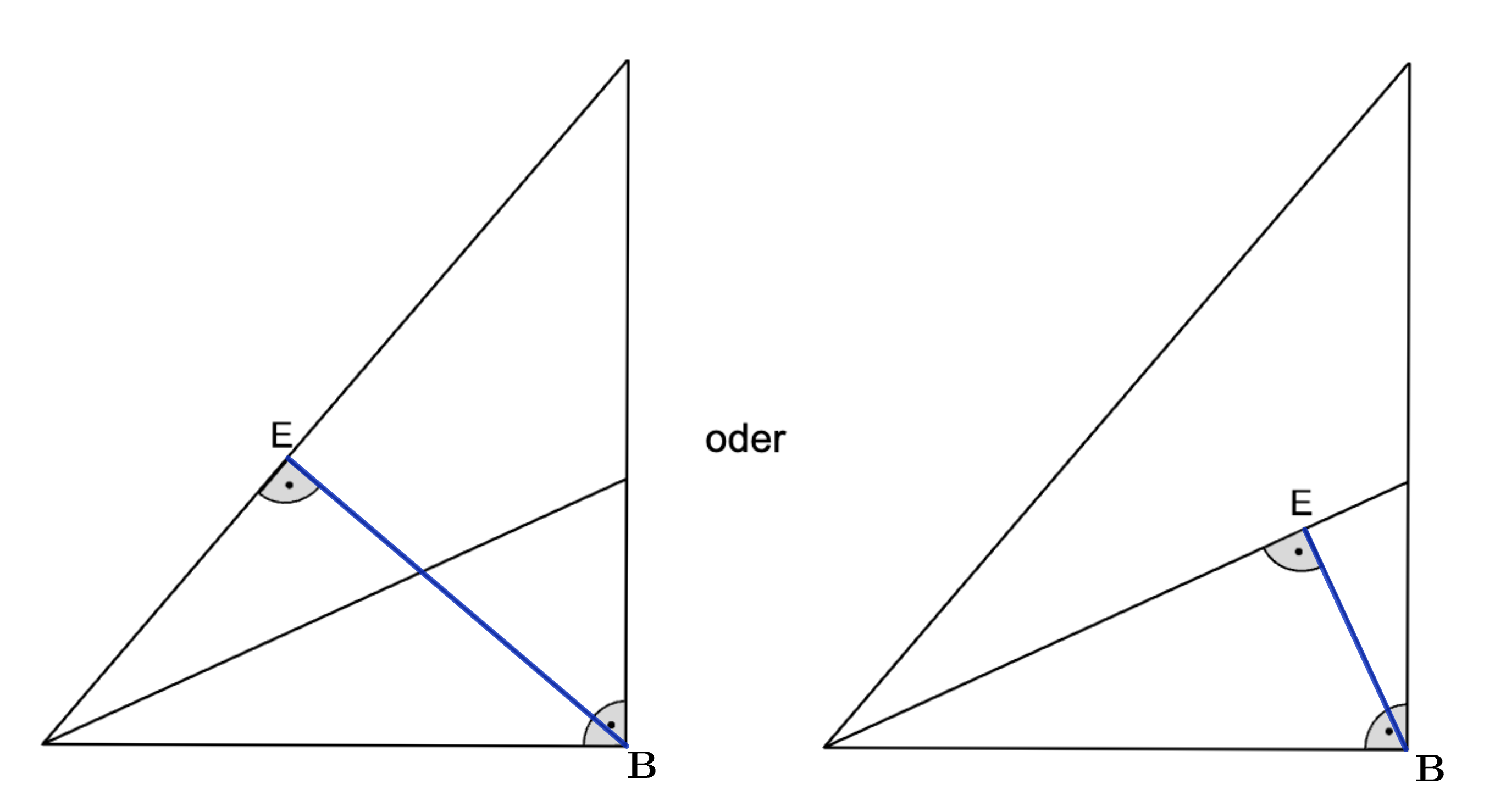
2. Skizzieren Sie die Abbildung auf Ihr Lösungsblatt und zeichnen Sie genau
  eine Strecke $\mathrm{\overline {BE}}$ so ein, dass für eines der abgebildeten Dreiecke der
  Höhensatz und der Kathetensatz aufgestellt werden kann.
  /5
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Höhen- und Kathetensatz
  Einzeichnen der Strecke $\mathrm{\overline{BE}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Vereinfachen Sie den folgenden Term so weit wie möglich.
Es gilt: x, y, z ≠ 0
$\displaystyle \frac{9x^{-2}y\cdot4y^2z^{-3}\cdot5x^7y^{-1}z}{2y^2\cdot3x^{-2}y^{-1}\cdot2x^1z^{-2}}$
/2
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
Vereinfachen des Terms.
$\mathrm{\dfrac{9x^{-2}y\cdot4y^2z^{-3}\cdot5x^7y^{-1}z}{2y^2\cdot3x^{-2}y^{-1}\cdot2x^1z^{-2}}}$
$\text{\color{green}{ordne}}$
$\mathrm{\displaystyle\frac{9\cdot4\cdot5\cdot x^7\cdot x^{-2}\cdot y^2\cdot y\cdot y^{-1}\cdot z\cdot z^{-3}}{2\cdot2\cdot3\cdot x\cdot x^{-2}\cdot y^2\cdot y^{-1}\cdot z^{-2}}}$
$\text{\color{green}{kürze}}$
$\mathrm{\dfrac{\cancel{9}\ {3}\cdot 5\cdot \cancel{4}\cdot x^7\cdot x^{-2}\cdot y^2\cdot y\cdot y^{-1}\cdot z\cdot z^{-3}}{\cancel{2}\cdot \cancel{2}\cdot \cancel{3}\cdot x\cdot x^{-2}\cdot y^2\cdot y^{-1}\cdot z^{-2}}}$
$\text{\color{green}{fasse zusammen}}$
$\mathrm{\displaystyle\frac{15\cdot\left(x^{7-2}\right)\cdot\left(y^{2+1-1}\right)\cdot\left(z^{1-3}\right)}{\left(x^{1-2}\right)\cdot\left(y^{2-1}\right)\cdot z^{-2}}}$
$\text{\color{green}{vereinfache}}$
$\mathrm{15\cdot x^{(7-2+1)}\cdot y^{(2-1)}\cdot z^{(-2+2)}}$
$\text{{Vereinfachter Term:}}\ \Rightarrow\ \boxed{\mathrm{15x^6y}}$
Ordne den Term
Vereinfache
Kürze
Fasse zusammen

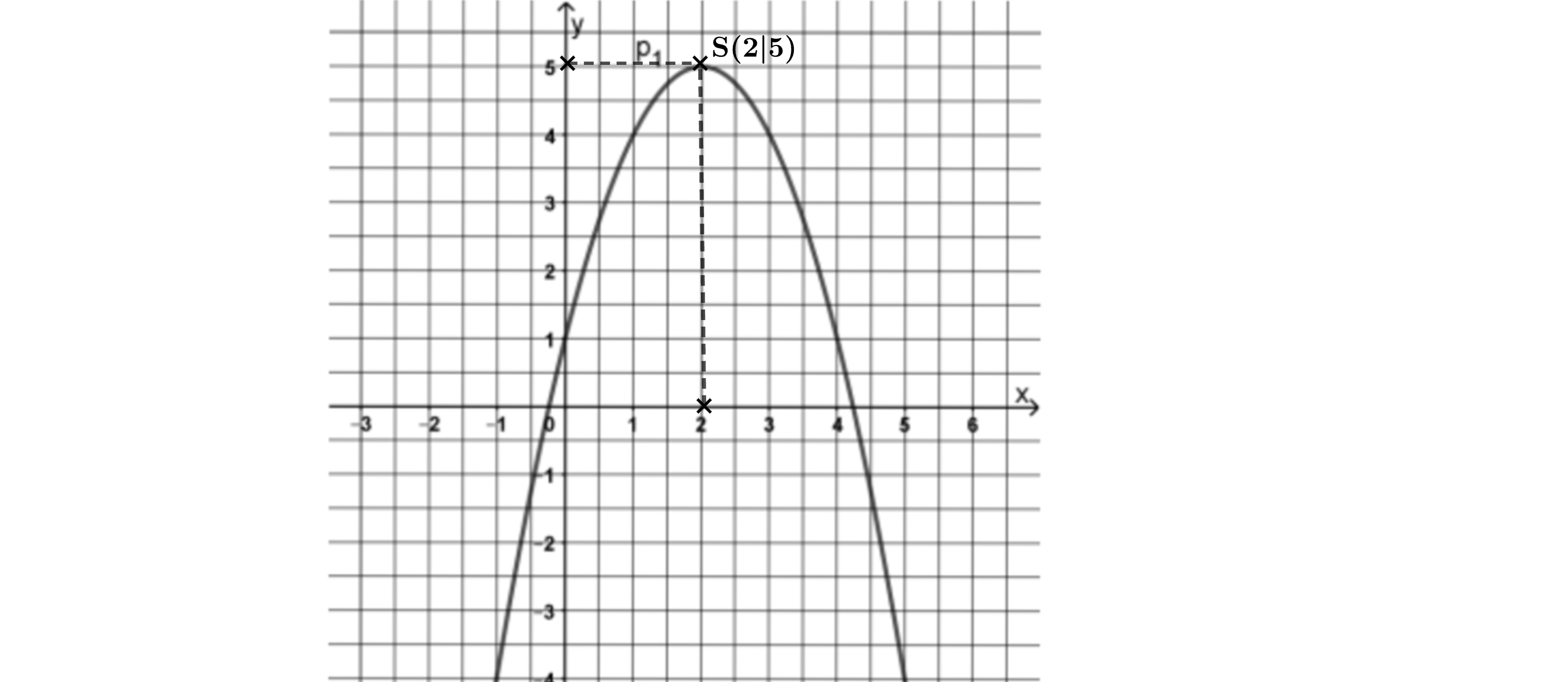
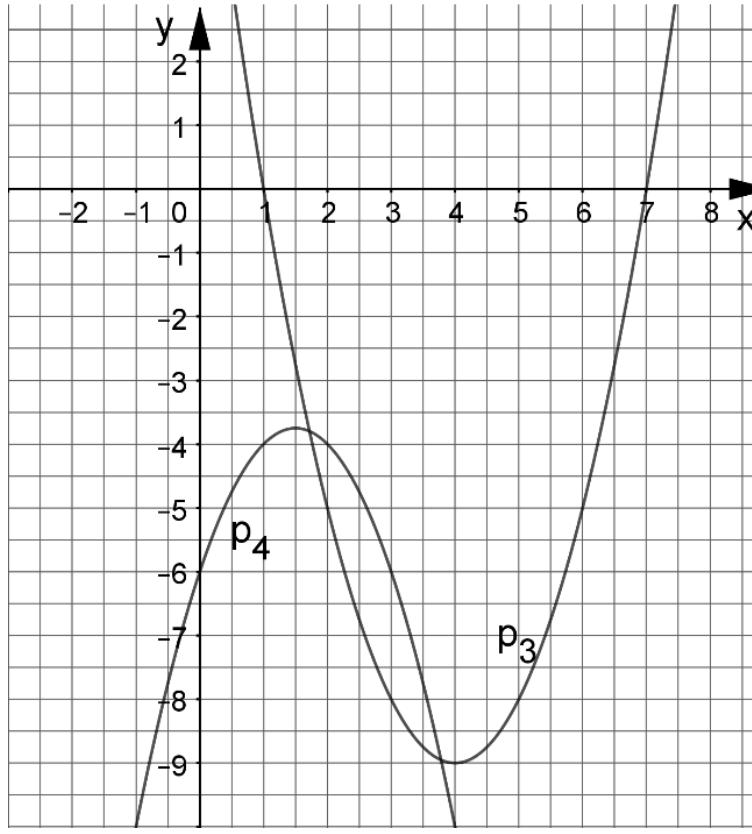
Die nachfolgende Abbildung zeigt die Parabel $\mathrm{p_1}.$
Ermitteln Sie rechnerisch die Funktionsgleichung von $\mathrm{p_1}$ in der Normalform.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Allgemeine Form und Scheitelform einer quadratischen Funktion
Rechnerische Ermittlung der Funktionsgleichung von $\mathrm{p_1}$ in der Normalform.
Der Scheitel der Parabel $\mathrm{p_{\tiny 1}}\$ ist laut Abbildung: $\ \mathrm{S_{\tiny 1}(2|5)}\$
Die Scheitelform lautet:
$\ \mathrm{f\left(x\right)=a(x-d)^2+e}$
Einsetzen der Koordinaten des Scheitelpunkts in die Scheitelform.
$\mathrm{p_1:\ y=-(x-2)^2+5}$
Da es sich um eine nach unten geöffnete Normalparabel handelt, ist der Öffnungsfaktor $\mathrm{a=-1}$
ausmultiplizieren der Scheitelform:
$\mathrm{y=-(x^2-4x+4)+5}$
auflösen der Klammer und zusammenfassen:
$\mathrm{y=-x^2+4x+1}$
die Normalform ist dann:
$\boxed{\mathrm{p_1\ :\ y=-x^2+4x+1}}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Koordinaten des Scheitelpunkts ablesen
Koordinaten in die Scheitelform einsetzen
Scheitelform ausmultiplizieren
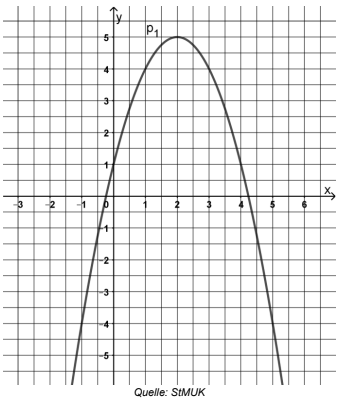
Die Parabel $p_{1}$ wird an der $x$ -Achse gespiegelt.
Geben Sie die Funktionsgleichung dieser gespiegelten Parabel $p_{2}$ in der
Scheitelpunktform an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsgraphen spiegeln
Ermitteln der Funktionsgleichung der, an der x-Achse gespiegelten Parabel $\mathrm{p_1}$ .
$\mathrm{p_1:\ y=-(x-2)^2+5}$
Spiegeln der Parabel $\mathrm{p_1}$ an der $\text{x}$ -Achse.
$\mathrm{p_2\ :\ y=-1\cdot\left[-(x-2)^2+5)\right]}$
$\mathrm{p_2\ :\ y=(x-2)^2-5}$
Die Scheitelform der Parabel $\mathrm{p_2}$ ist dann:
$\boxed{\mathrm{y=(x-2)^2-5}}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für die Spiegelung an der $x$ -Achse muss der Funktionsterm mit $- 1$ multipliziert werden.
Multipliziere den Funktionsterm mit $- 1$
Die Parabel $\mathrm{p_3:y=x^2-8x+7}$ schneidet die $x$ -Achse in den Punkten
$\mathrm{N_1}$ und $\mathrm{N_2}$ .
Berechnen Sie die $x$ -Koordinaten dieser beiden Punkte.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
Berechnen der $x$ -Koordinaten der Punkte $\mathrm{N_1}$ und $\mathrm{N_2}$ .
Anwenden der Mitternachtsformel.
Die Mitternachtsformel lautet:
$\mathrm{x_{1{,}2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}}$
Einsetzen der Werte aus $\mathrm{p_3}$ .
$\mathrm{x_{1{,}2}=\dfrac{8\pm\sqrt{(-8)^2-4\cdot 1\cdot 7}}{2\cdot 1}}$
$\mathrm{x_{1{,}2}=\dfrac{8\pm\sqrt{36}}{2\cdot 1}}$
$\mathrm{x_{1}=\dfrac{8-6}{2\cdot 1}\ \Rightarrow\ x_1=1}$
$\mathrm{x_{2}=\dfrac{8+6}{2\cdot 1}\ \Rightarrow\ x_2=7}$
Die x-Koordinaten der Punkte $\mathrm{N_1}$ und $\mathrm{N_2}$ sind:
$\boxed{\mathrm{x_1=1}}\qquad\boxed{\mathrm{ x_2=7}}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Setze $\mathrm{y=0}$
Berechne $\text{x}$ mit der Mitternachtsformel
Überprüfen Sie rechnerisch, ob die Punkte $A (4 ∣ - 8)$ und $B (10 ∣ 27)$ auf der
Parabel $p_{3}$ liegen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
Überprüfen, ob die Punkte $\mathrm{A(4|−8)}$ und $\mathrm{B(10|27)}$ auf der Parabel $\mathrm{p_3}$ liegen.
Einsetzen der $\text{x}$ -Koordinaten des Punkts $\text{A}$ in $\mathrm{p_3}$ .
$\mathrm{y=4^2-8\cdot 4+7}$
$\mathrm{y=-9\quad\Rightarrow\quad}$ Der Punkt $\text{A}$ liegt nicht auf der Parabel $\mathrm{p_3}$ .
Einsetzen der $\text{x}$ -Koordinaten des Punkts $\text{B}$ in $\mathrm{p_3}$ .
$\mathrm{y=10^2-8\cdot 10+7}$
$\mathrm{y=27\quad\Rightarrow\quad}$ Der Punkt $\text{B}$ liegt auf der Parabel $\mathrm{p_3}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Setze die $\text{x}$ -Koordinaten der Punkte $\text{A}$ und $\text{B}$ ind Funktionsgleichung von $\mathrm{p_3}$ ein.
Berechne $\text{y}$
Vergleiche die $\text{y}$ -Werte.

Die Gerade $\mathrm{g:y=x−9}$ schneidet die Parabel $\mathrm{p_4:y=−x^2+3x-6}\ \$ in den

Punkten $\text{C}$ und $\text{D}$ .

Ermitteln Sie rechnerisch die Koordinaten dieser Schnittpunkte und geben

Sie $\text{C}$ und $\text{D}$ an.

Zeichnen Sie die Parabeln $\mathrm{p_3}$ und $\mathrm{p_4}$ in ein Koordinatensystem mit der
Längeneinheit $1\cm$ .
/7

Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel zeichnen
Einzeichnen der Parabeln $\mathrm{p_3}$ und $\mathrm{p_4}$ in ein Koordinatensystem.
Die Abbildung ist nicht maßtreu.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

5
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
In einer beliebten Urlaubsregion gab es im Jahr 2010 insgesamt $88$ Millionen Übernachtungen. In den folgenden neun Jahren ist die Zahl der Übernachtungen exponentiell auf $101$ Millionen im Jahr 2019 gestiegen.
1. Berechnen Sie den jährlichen Zuwachs in diesen neun Jahren in Prozent.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
  Berechnen des jährlichen Zuwachses in Prozent.
  Die Formel zur Berechnung des exponentiellen Wachstum lautet:
  $\mathrm{N(t)=N_0\cdot a^t\ ;\qquad a=(1+p)}$
  Die folgenden Größen sind bekannt:
  $\mathrm{N_0=88}$ Millionen; $\mathrm{\qquad N(t)=101}$ Millionen; $\mathrm{\qquad t=9}$ Jahre
  Wir berechnen $\text{a}$ , indem wir die Werte in die Formel einsetzen:
  $\mathrm{101=88\cdot a^9\ \Rightarrow\ a=\sqrt[9]{\dfrac{101}{88}}}$
  $\mathrm{a\approx1{,}0154}$
  Jetzt können wir den Zuwachs $\text{p}$ in Prozent berechnen:
  $\mathrm{a=(1+p)\ \Rightarrow\ p=a-1}$
  $\mathrm{p=1{,}0154-1\ \Rightarrow\ p=0{,}0154}$
  Der jährliche Zuwachs beträgt dann: $\boxed{1{,}54\ \%}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Wachstumsfaktor $\text{q}$ .
  Berechne den jährlichen Zuwachs $\text{p}$ in Prozent.
2. In den zwei Jahren ab 2019 nahm die Zahl der Übernachtungen um jährlich $22,3$ % ab.
  Berechnen Sie die Zahl der Übernachtungen nach diesen zwei Jahren.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
  Berechnen der Zahl der Übernachtungen nach zwei Jahren.
  Die Formel zur Berechnung des exponentiellen Zerfalls lautet:
  $\mathrm{N(t)=N_0\cdot a^t\ ;\qquad a=(1-p)}$
  Die folgenden Größen sind bekannt:
  $\mathrm{N_0=101}$ Millionen; $\quad \mathrm{p=22{,}3\ \%};$ $\quad\mathrm{t=2}$ Jahre
  berechnen von $\text{a}$
  $\mathrm{a=1-0{,}223\ \Rightarrow\ a=0{,}777}$
  berechnen von $\mathrm{N(2)}$
  $\mathrm{N(2)=101\cdot 0{,}777^2\ \Rightarrow\ N(2)=60{,}98}$
  Die Zahl der Übernachtungen nach diesen zwei Jahren im Jahr 2021
  beträgt ungefähr: $\boxed{61}$ Millionen
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Zerfallsfaktor $\text{a}$
  Berechne die Anzahle der Übernachtungen nach 2 Jahren
3. Von 2021 bis 2022 stieg die Übernachtungszahl wieder um $1,65$ % auf $62$ Millionen an.
  Berechnen Sie, wie viele Jahre es bei diesem jährlichen prozentualen Zuwachs noch dauern würde, bis die Übernachtungszahl von $101$ Millionen wieder erreicht würde.
  /4
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
  Berechnen Anzahl Jahre.
  Zur Berechnung der Anzahl der Jahre verwenden wir die Formel aus Teilaufgabe a.)
  $\mathrm{N(t)=N_0\cdot a^t}$
  Die folgenden Größen sind bekannt:
  $\mathrm{N(t)=101}$ Millionen; $\quad\mathrm{N_0=62}$ Millionen; $\quad\mathrm{a=1+0{,}0165=1{,}0165}$
  berechnen von $\text{t}$
  $\mathrm{101=62\cdot 1{,}0165^t\ \Rightarrow\ t=\dfrac{lg101-lg62}{lg1{,}0165}}$
  $\hspace{35mm}\boxed{\mathrm{t\approx30}}$
  Bei einem jährlichen Zuwachs von $1{,}65\ \%$ dauert es ungefähr
  $30$ Jahre bis die Übernachtungszahl von $101$ Millionen wieder erreicht wird.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Berechnen Sie für folgende Längen die Höhe des Baumes (siehe Skizze):

$\text{a} = 20\cm$ , $\text{b} = 25\cm$ , $\text{c} = 20\m$ , $\text{d=1{,}60\m}$

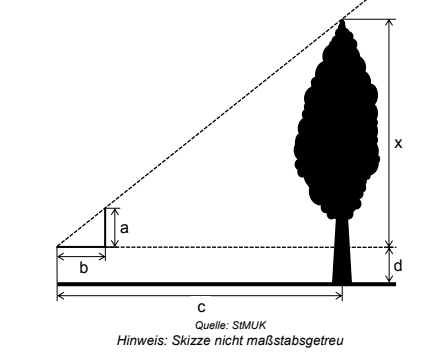
7
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Eine Messingkugel soll in einem würfelförmigen Behälter aufbewahrt werden.
Der Würfel hat ein Innenvolumen von $100 \cm^3$ . Die Kugel hat eine Masse
von $550\ \text{g}$ , wobei $1 \cm^3$ Messing eine Masse von $8{,}73\ \text{g}$ hat.
Begründen Sie nachvollziehbar, ob die Kugel in den Behälter passt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenformeln
Berechnen der Kantenlänge des Würfels.
Die Formel zur Berechnung des Volumens eines Würfels lautet:
$\mathrm{V_{Würfel}=a\cdot a\cdot a=a^3}$
Wir lösen die Formel nach $\text{a}$ auf.
$\mathrm{a=\sqrt[3]{V_{Würfel}}}$
$\mathrm{a=\sqrt[3]{100}\ \ cm\ \Rightarrow\ a\approx 4{,}64\cm}$
Berechnen des Durchmessers der Kugel.
Von der Kugel sind folgende Größen bekannt,
die Masse der Kugel $\mathrm{m=550\ g}$ und die Masse von $1\cm^3$ Messing $=8{,}73\ \text{g}$
d.h. die Dichte von Messing beträgt: $\mathrm{\rho=8{,}73\dfrac{g}{cm^3}}$
Damit wir den Durchmesser der Kugel berechnen können, müssen wir zuerst das Volumen der Kugel mithilfe der bekannten Größen berechnen.
Die Formel zur Berechnung der Dichte lautet:
$\mathrm{\rho=\dfrac{m}{V}}$ ; wir lösen die Formel nach $\text{V}$ auf.
$\mathrm{V=\dfrac{m}{\rho}}$ ; wir setzen die bekannten Größen ein und berechnen das Volumen der Kugel.
$\mathrm{V_{Kugel}=\dfrac{550\ \cancel{g}\cdot cm^3}{8{,}73\ \cancel{g}}\ \Rightarrow\ V_{Kugel}\approx63\ cm^3}$
Jetzt können wir den Durchmesser der Kugel berechnen, wir lösen die Formel
$\boxed{\mathrm{V_{Kugel}=\dfrac{4}{3}\cdot r^3\cdot \pi}}$ nach $\text{r}$ auf.
$\mathrm{r=\sqrt[3]{\dfrac{3\cdot V_{Kugel}}{4\cdot \pi}}}$
$\mathrm{r=\sqrt[3]{\dfrac{3\cdot 63\ cm^3}{4\cdot \pi}}\ \Rightarrow\ r\approx2{,}47\ cm}$
Der Durchmesser der Kugel beträgt dann ungefähr $4{,}94\cm$ .
Die Kugel passt also nicht in den Würfel, da der Durchmesser der Kugel größer ist, als die Kantenlänge des Würfels.
Berechne die Kantenlänge des Würfels.
Berechne den Durchmesser der Kugel
Vergleiche die Kantenlänge des Würfels mit dem Durchmesser der Kugel.

Geben Sie die Definitionsmenge der folgenden Gleichung an und ermitteln Sie

die Lösungsmenge rechnerisch.

_/3

\displaystyle \dfrac{32}{8x+16}=\dfrac{5x}{2x+4}

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen lösen

Bestimmen der Definitionsmenge.

Im Nenner eines Bruches darf nicht Null stehen. Alle Zahlen, für die sich beim Einsetzen in die Gleichung im Nenner Null ergibt, dürfen nicht in der Definitionsmenge enthalten sein.

Setze jeden der Nenner gleich Null.

$\mathrm{8x+16=0}$

$\mathrm{8x=-16\ \Rightarrow\ x=-2}$

$\mathrm{2x+4=0}$

$\mathrm{2x=-4\ \Rightarrow\ x=-2}$

Der Nenner wird Null bei:

$\mathrm{x=-2\qquad\Rightarrow\qquad D=\mathbb R\setminus \left\{-2\right\}}$

Lösen der Bruchgleichung:

$\dfrac{32}{8x+16}=\dfrac{5x}{2x+4}$

Über Kreuz multiplizieren
	↓
$\displaystyle 32\cdot (2x+4)$	$=$	$\displaystyle \mathrm{5x\cdot (8x+16)}$
	↓	Klammern auflösen
$\displaystyle \mathrm{64x+128}$	$=$	$\displaystyle \mathrm{40x^2+80x}$
	↓	ordnen und zusammenfassen
$\displaystyle \mathrm{40x^2+16x-128}$	$=$	$\displaystyle 0$	$\displaystyle :40$
	↓	vereinfachen
$\displaystyle \mathrm{x^2+0{,}4x-3{,}2}$	$=$	$\displaystyle 0$

Benutze zur Lösung der quadratischen Gleichung die Mitternachtsformel.

Die Mitternachtsformel lautet:

$\mathrm{x_{1{,}2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}}$

einsetzen der Werte in die Mitternachtsformel und berechnen von $\mathrm{x_{1{,}2}}$

$\mathrm{x_{1{,}2}=\dfrac{-0{,}4\pm\sqrt{0{,}16+12{,}8}}{2}}$

$\mathrm{x_{1{,}2}=\dfrac{-0{,}4\pm\sqrt{12{,}96}}{2}}$

$\mathrm{x_{1{,}2}=\dfrac{-0{,}4\pm{3{,}6}}{2}\ \Rightarrow\ x_{1}=-2}\quad$ und $\quad \mathrm{x_{2}=1{,}6}$

$\mathrm{x_1}$ müssen wir als Lösung ausschließen, da $- 2$ nicht in der Definitionsmenge enthalten ist.

Die Lösungsmenge ist dann: $\ \mathbb{L}=\{1{,}6\}$

Alternative Lösung zur Bestimmung der Lösungsmenge

Kürze den ersten Bruch mit $4$ , dann wird

$\displaystyle \dfrac{32}{8x+16}=\dfrac{5x}{2x+4}$ zu $\displaystyle \dfrac{8}{2x+4}=\dfrac{5x}{2x+4}$ .

Zwei Brüche mit demselben Nenner sind genau dann gleich, wenn die Zähler gleich sind, also $8 = 5 x$ . Division durch $5$ ergibt $x = 1,6$ , also $\L=\{1{,}6\}.$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

9
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Bei einem Zufallsexperiment befinden sich in einem Behälter $20$ Kugeln.
Auf jede Kugel ist genau eine Zahl aufgedruckt:
Viermal die Zahl $1$ , sechsmal die Zahl $2$ und zehnmal die Zahl $3$ .
Nacheinander wird jeweils eine Kugel gezogen und nicht mehr zurückgelegt.
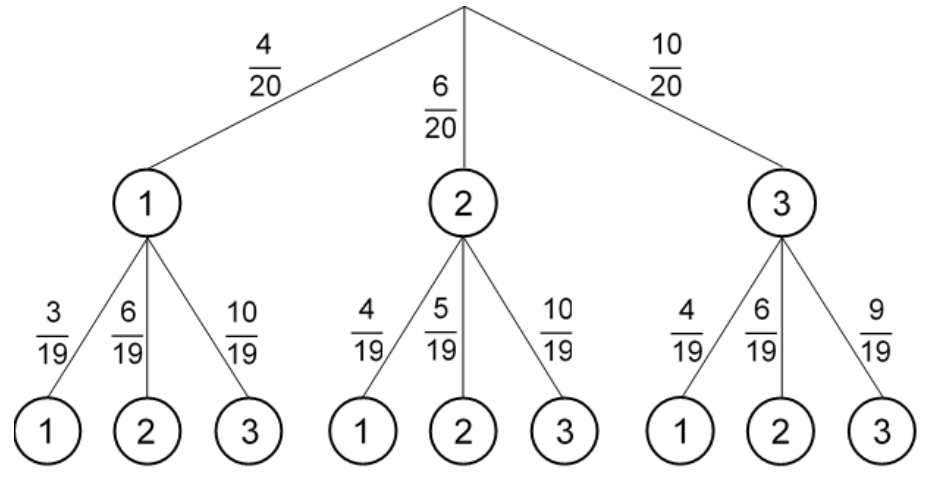
1. Es wird zweimal gezogen.
  Stellen Sie diesen Sachverhalt in einem Baumdiagramm dar und beschriften Sie die Äste mit den jeweiligen Wahrscheinlichkeiten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Baumdiagramm zeichnen:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
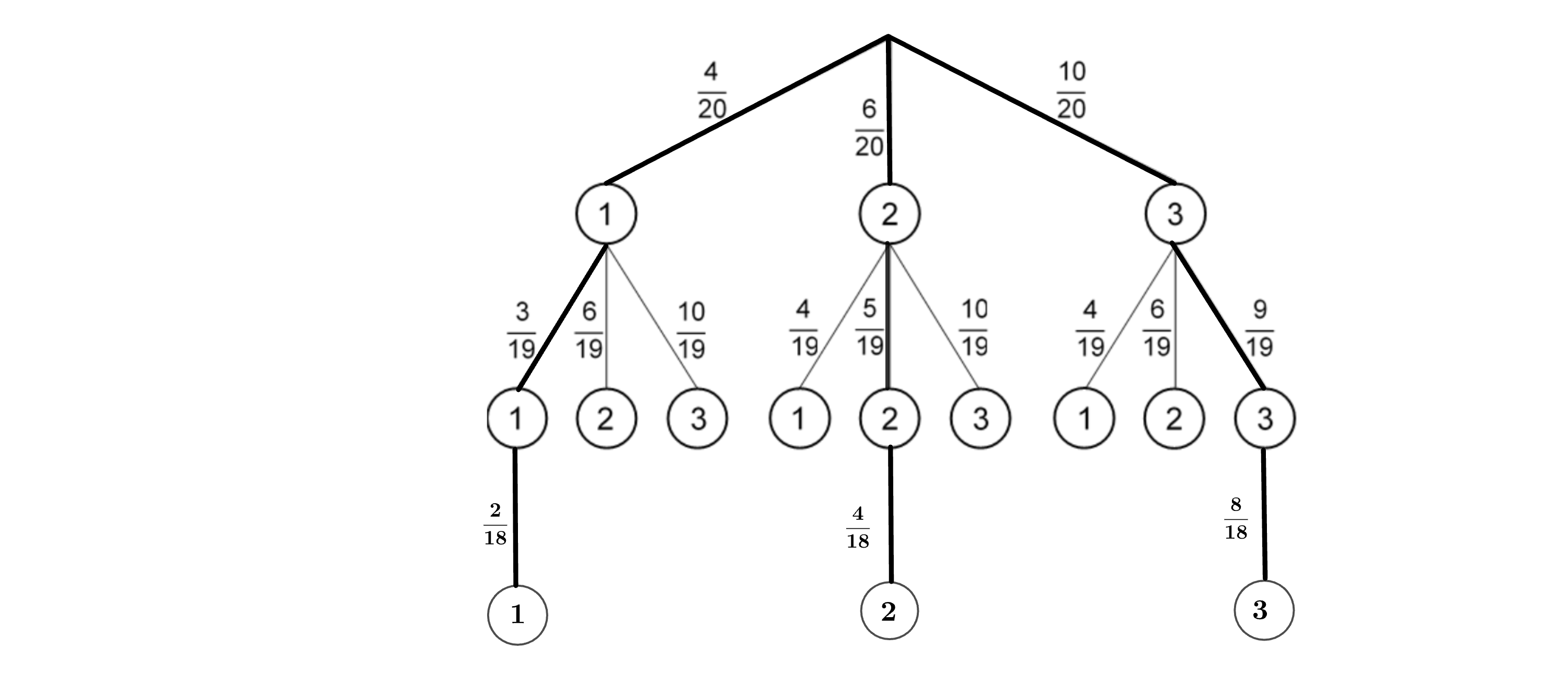
2. Es wird dreimal gezogen.
  Berechnen Sie die Wahrscheinlichkeit, dass dreimal die gleiche Zahl gezogen wird.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  Das Baumdiagramm braucht nicht gezeichnet zu werden.
  Wahrscheinlichkeit für drei gleiche Zahlen (anwenden der Produkt- und Summenregel)
  $\dfrac{4}{20}\cdot\dfrac{3}{19}\cdot\dfrac{2}{18}+\dfrac{6}{20}\cdot\dfrac{5}{19}\cdot\dfrac{4}{18}+\dfrac{10}{20}\cdot\dfrac{9}{19}\cdot\dfrac{8}{18}=$
  durch Kürzen und Zusammenfassen der Brüche erhält man dann:
  $\dfrac{1}{285}+\dfrac{1}{57}+\dfrac{2}{19}=\dfrac{1+5+30}{285}=\dfrac{36}{285}$
  Die Wahrscheinlichkeit dreimal die gleiche Zahlen zu ziehen beträgt dann,
  als Bruch: $\ \boxed{\text{P}=\dfrac{12}{95}}\quad$ als Dezimalzahl: $\ \boxed{\mathrm{P=0{,}1263}}\quad$ in Prozent: $\ \boxed{\mathrm{P=12{,}63\ \%}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Wende die $1$ . Pfadregel (Produktregel) und die $2$ . Pfadregel (Summenregel) an.
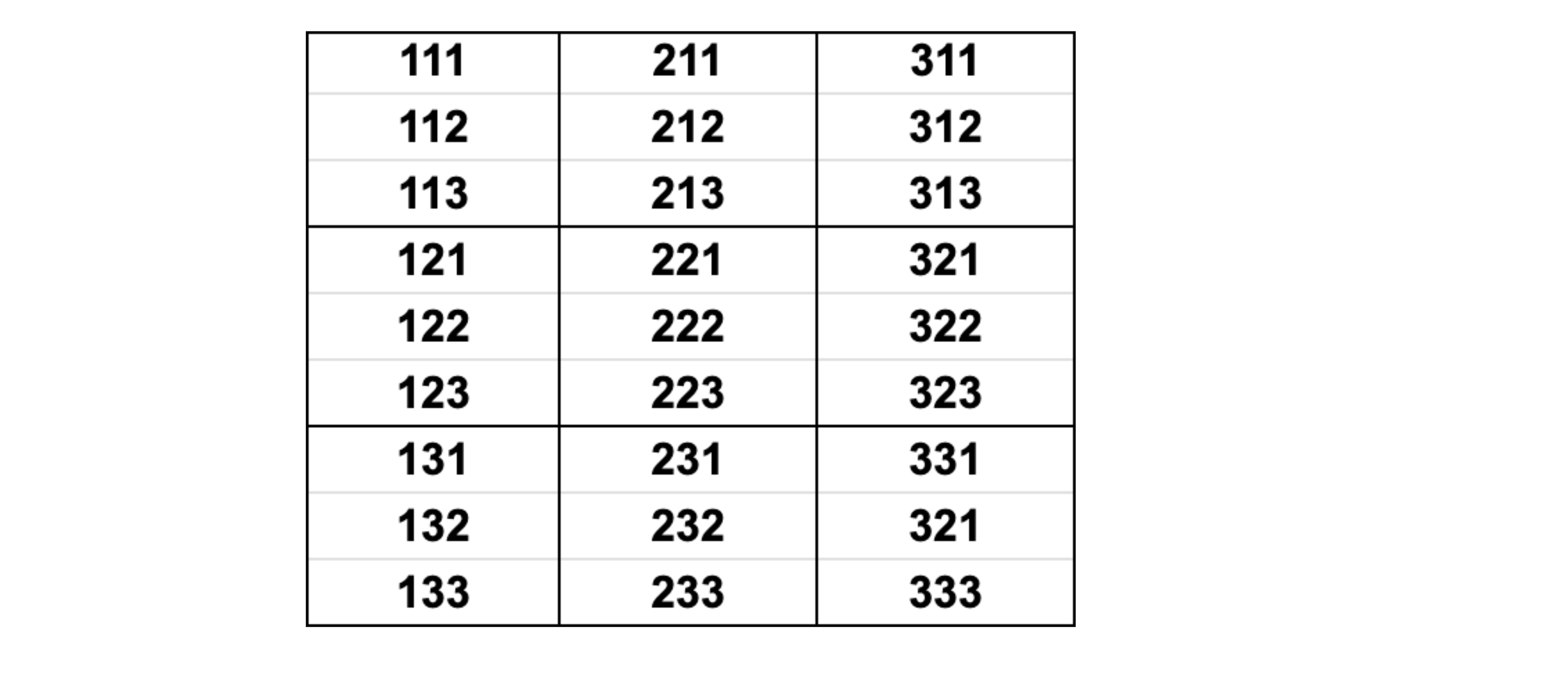
3. Es wird dreimal gezogen. Die drei Zahlen bilden in der gezogenen Reihenfolge eine dreistellige Zahl.
  Berechnen Sie, wie viele unterschiedliche dreistellige Zahlen auftreten
  können.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Aufgaben zur Kombinatorik im typischen Sinn
  Tabelle der möglichen Zahlen
  Die Tabelle braucht nicht erstellt zu werden.
  Berechnen der Anzahl der Kombinationen:
  $3\cdot 3\cdot 3=27$
  Es können $\boxed{27}$ unterschiedliche dreistellige Zahlen auftreten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
10
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Folgende Gleichungen sind Anwendungen von binomischen Formeln.
Stellen Sie die vollständigen Gleichungen auf und notieren Sie diese auf Ihrem Lösungsblatt.
1. $\square-\square+169y^6=(9x-\square)^2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomische Formeln
  $2$ . Binomische Formel:
  $\mathrm{a^2-2ab+b^2=\ \ (a-b)^2}$
  Anwenden der $2$ . Binomischen Formel auf:
  $\square-\square+169y^6=(9x-\square)^2$
  $\mathrm{a^2=81x^2}\ \$ und $\mathrm{b=13y^3}\mathrm{\left(\sqrt{169y^6}\right)}\quad \mathrm{2ab=2\cdot 9x\cdot 13y^3=234xy^3}$
  Einsetzen der Werte in die Lücken.
  $\boxed{\mathrm{81x^2}}-\boxed{\mathrm{234xy^3}}+\mathrm{169y^6}=\left(\mathrm{9x}-\boxed{\mathrm{13y^3}}\right)^2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Anwenden der $2.$ Binomischen Formel.
2. $-(\square-15y)^2=-49x^2\square210xy\square225y^2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomische Formeln
  $\mathrm{-(a-b)^2=-(a^2-2ab+b^2)}$
  $\mathrm{-(a-b)=-a^2+2ab-b^2}$
  $-(\square-15y)^2=-49x^2\square210xy\square225y^2$
  Ergänzen der Lücken liefert:
  $-\left(\boxed{\mathrm{7x}}-15\text{y}\right)^2=-49\mathrm{x^2}\boxed{+}210\text{xy}\boxed{-}225\mathrm{y^2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Anwenden der $2$ . Binomischen Formel
  Vorzeichen ändern

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Gleichsetzen der Geradengleichungen
	↓
$\displaystyle \mathrm{3x-3}$	$=$	$\displaystyle \mathrm{-x-1}$	$\displaystyle +\text{x}$
	↓	addieren
$\displaystyle \mathrm{4x-3}$	$=$	$\displaystyle -1$	$\displaystyle +3$
	↓	subtrahieren
$\displaystyle \mathrm{4x}$	$=$	$\displaystyle 2$	$\displaystyle :4$
	↓	dividieren
$\displaystyle \text{x}$	$=$	$\displaystyle 0{,}5$

$\displaystyle \mathrm{−x^2+3x-6}$	$=$	$\displaystyle \mathrm{x-9}$	$\displaystyle -x+9$
$\displaystyle \mathrm{−x^2+2x+3}$	$=$	$\displaystyle 0$

berechnen von $x$
	↓
$\displaystyle \dfrac{20}{0{,}25}$	$=$	$\displaystyle \dfrac{\text{x}}{0{,}20}$	$\displaystyle \cdot 0{,}20$
	↓	multiplizieren
$\displaystyle \dfrac{20\cdot 0{,}20}{0{,}25}$	$=$	$\displaystyle \text{x}$
	↓	ausmultiplizieren und Seiten tauschen
$\displaystyle \text{x}$	$=$	$\displaystyle 16$

Teil B-Aufgabengruppe I

Ermitteln der Funktionsgleichung der Geraden g1\mathrm{g_1}g1​

Hast du eine Frage oder Feedback?

Überprüfen, ob der Punkt C\text{C}C auf g2\mathrm{g_2}g2​ liegt.

Hast du eine Frage oder Feedback?

Ermitteln Sie die Funktionsgleichung der Geraden g3g_3g3​.

Hast du eine Frage oder Feedback?

Berechnen der x\text{x}x-Koordinate des Schnittpunkts N4\mathrm{N_4}N4​.

Hast du eine Frage oder Feedback?

Ermitteln der Koordinaten des Schnittpunkts S\text{S}S der Geraden g2\mathrm{g_2}g2​ und g4\mathrm{g_4}g4​.

Hast du eine Frage oder Feedback?

Verändern einer Zahl in einer der beiden Funktionsgleichungen so, dass die beiden Geraden mindestens einen Punkt gemeinsam haben.

Hinweis:

Hast du eine Frage oder Feedback?

Einzeichnen der Geraden g2\mathrm{g_2}g2​ und g4\mathrm{g_4}g4​ in ein Koordinatensystem.

Hast du eine Frage oder Feedback?

Berechnen des Flächeninhalts des Dreiecks ACD\text{ACD}ACD.

Hast du eine Frage oder Feedback?

Einzeichnen der Strecke BE‾\mathrm{\overline{BE}}BE

Hast du eine Frage oder Feedback?

Vereinfachen des Terms.

Rechnerische Ermittlung der Funktionsgleichung von p1\mathrm{p_1}p1​ in der Normalform.

Hast du eine Frage oder Feedback?

Ermitteln der Funktionsgleichung der, an der x-Achse gespiegelten Parabel p1\mathrm{p_1}p1​.

Hast du eine Frage oder Feedback?

Berechnen der xxx-Koordinaten der Punkte N1\mathrm{N_1}N1​ und N2\mathrm{N_2}N2​.

Hast du eine Frage oder Feedback?

Überprüfen, ob die Punkte A(4∣−8)\mathrm{A(4|−8)}A(4∣−8) und B(10∣27)\mathrm{B(10|27)}B(10∣27) auf der Parabel p3\mathrm{p_3}p3​ liegen.

Hast du eine Frage oder Feedback?

Berechnen der Koordinaten der Schnittpunkte von g\text{g}g und p4\mathrm{p_4}p4​ .

Hast du eine Frage oder Feedback?

Einzeichnen der Parabeln p3\mathrm{p_3}p3​ und p4\mathrm{p_4}p4​ in ein Koordinatensystem.

Hast du eine Frage oder Feedback?

Berechnen des jährlichen Zuwachses in Prozent.

Hast du eine Frage oder Feedback?

Berechnen der Zahl der Übernachtungen nach zwei Jahren.

Hast du eine Frage oder Feedback?

Berechnen Anzahl Jahre.

Hast du eine Frage oder Feedback?

Berechnen der Baumhöhe in [m].

Berechnen der Kantenlänge des Würfels.

Berechnen des Durchmessers der Kugel.

Bestimmen der Definitionsmenge.

Lösen der Bruchgleichung:

Baumdiagramm zeichnen:

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit für drei gleiche Zahlen (anwenden der Produkt- und Summenregel)

Hast du eine Frage oder Feedback?

Tabelle der möglichen Zahlen

Berechnen der Anzahl der Kombinationen:

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Ermitteln der Funktionsgleichung der Geraden $\mathrm{g_1}$

Überprüfen, ob der Punkt $\text{C}$ auf $\mathrm{g_2}$ liegt.

Ermitteln Sie die Funktionsgleichung der Geraden $g_{3}$ .

Berechnen der $\text{x}$ -Koordinate des Schnittpunkts $\mathrm{N_4}$ .

Ermitteln der Koordinaten des Schnittpunkts $\text{S}$ der Geraden $\mathrm{g_2}$ und $\mathrm{g_4}$ .

Einzeichnen der Geraden $\mathrm{g_2}$ und $\mathrm{g_4}$ in ein Koordinatensystem.

Berechnen des Flächeninhalts des Dreiecks $\text{ACD}$ .

Einzeichnen der Strecke $\mathrm{\overline{BE}}$

Rechnerische Ermittlung der Funktionsgleichung von $\mathrm{p_1}$ in der Normalform.

Ermitteln der Funktionsgleichung der, an der x-Achse gespiegelten Parabel $\mathrm{p_1}$ .

Berechnen der $x$ -Koordinaten der Punkte $\mathrm{N_1}$ und $\mathrm{N_2}$ .

Überprüfen, ob die Punkte $\mathrm{A(4|−8)}$ und $\mathrm{B(10|27)}$ auf der Parabel $\mathrm{p_3}$ liegen.

Berechnen der Koordinaten der Schnittpunkte von $\text{g}$ und $\mathrm{p_4}$ .

Einzeichnen der Parabeln $\mathrm{p_3}$ und $\mathrm{p_4}$ in ein Koordinatensystem.