Gegeben sind die Geraden , und sowie die Punkte
und .
Die Gerade verläuft parallel zur -Achse und durch den Punkt .
Die Gerade verläuft durch die Punkte und .
Die Gerade schneidet im Punkt und steht senkrecht auf .
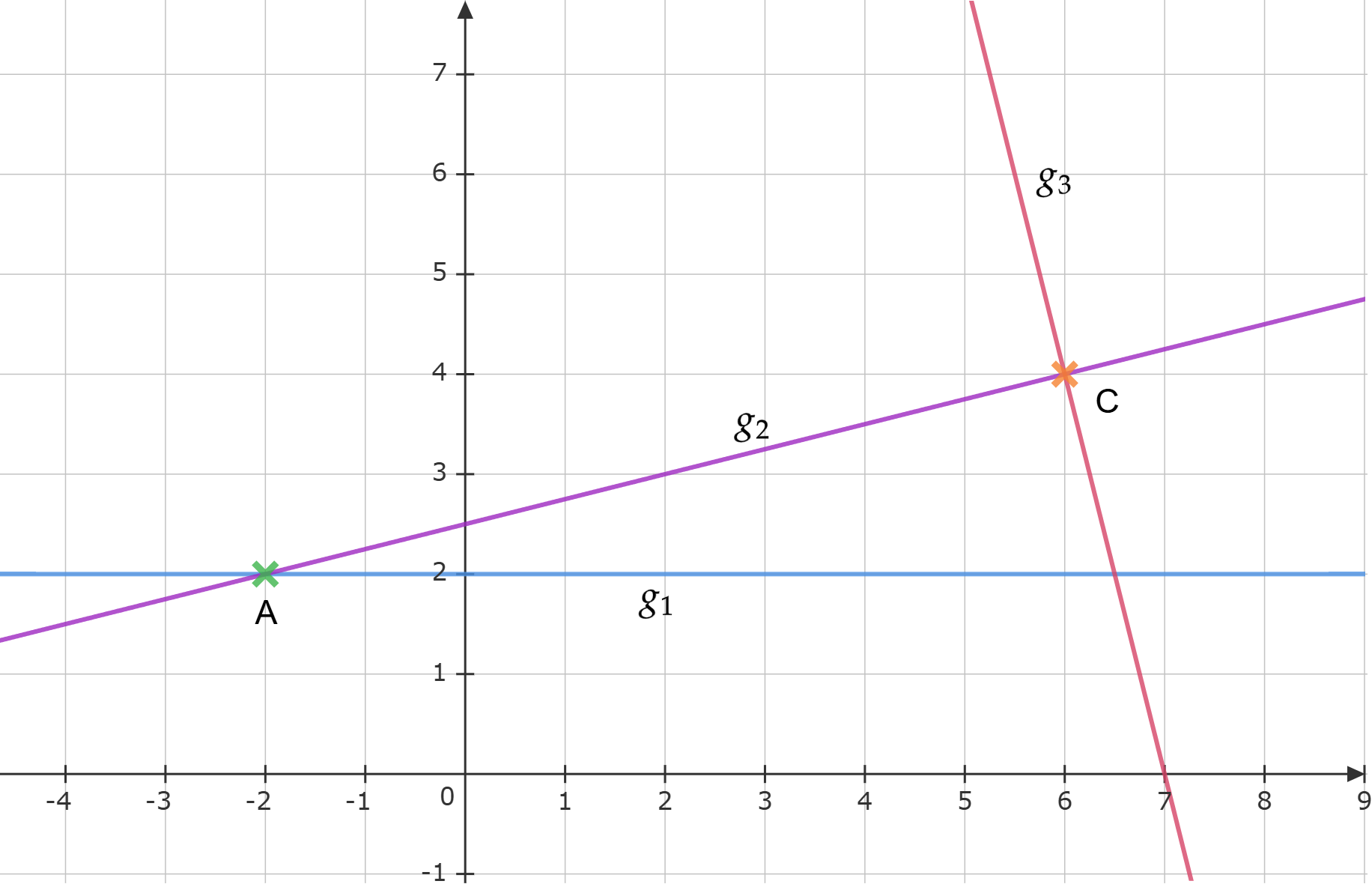
Zeichnen Sie die Geraden , und in ein Koordinatensystem mit
der Längeneinheit .
Berechnen Sie den Abstand zwischen den Punkten und .
Geben Sie die Funktionsgleichung der Geraden an.
Bestimmen Sie rechnerisch die Funktionsgleichung der Geraden .
Die Gerade mit der Funktionsgleichung : schneidet die
Gerade : im Punkt .
Ermitteln Sie rechnerisch die Koordinaten des Schnittpunkts