Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist die Funktion mit der Gleichung .
Für und ist die Funktionenschar gegeben durch die Gleichung
.
Es gilt .
Begründen Sie, dass alle Graphen von Funktionen der Schar nur einen Schnittpunkt mit der -Achse haben. (2 P)
Bestimmen Sie rechnerisch die Koordinaten und die Art des Extrempunktes des Graphen von in Abhängigkeit von . Zur Kontrolle: Die Extremstelle ist . (5 P)
Gegeben ist die Funktion mit für .
(i) Weisen Sie nach, dass alle Extrempunkte der Graphen der Funktionenschar auf dem Graphen der Funktion liegen. (2 P)
(ii) Geben Sie einen Punkt des Graphen der Funktion an, der kein Extrempunkt eines Graphen der Funktionenschar mit ist. (1 P)
Für liegt zwischen der -Achse und dem Graphen der Funktion die nach rechts offene Fläche .
Prüfen Sie rechnerisch, ob der Inhalt der Fläche vom Parameter abhängt. (3 P)
Die Graphen der Funktionen und schneiden sich nur im Punkt und in einem weiteren Punkt .
(i) Geben Sie die Koordinaten des Hochpunktes des Graphen von an und bestimmen Sie die Koordinaten des Schnittpunktes der Graphen von und .
(2 P)
(ii) Skizzieren Sie mithilfe dieser Punkte den Graphen der Funktion in Abbildung 3. (2 P)
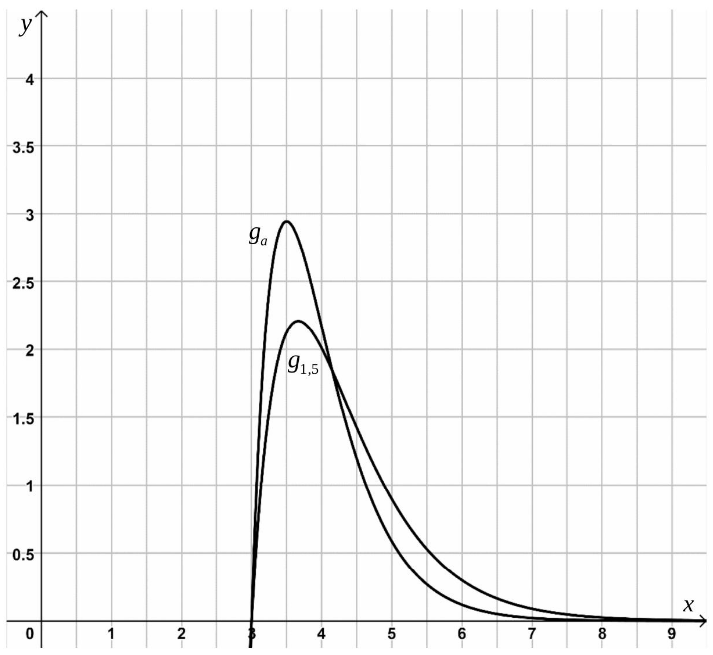
Abbildung 3
Für ein ist der Graph der Funktion in Abbildung 3 dargestellt.
Begründen Sie anhand des Hochpunktes ohne weitere Berechnung, ob der Wert von größer oder kleiner ist als . (2 P)
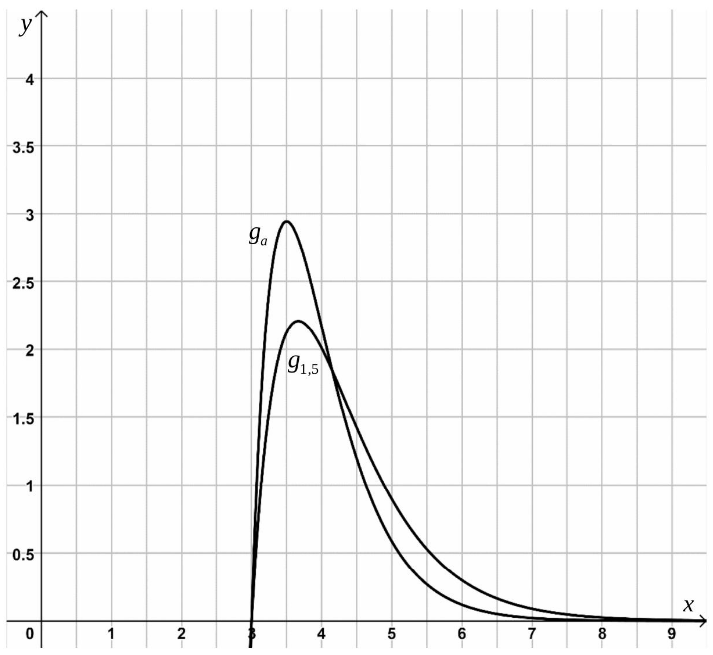
Abbildung 3

