1 Begründe, dass gilt:
Die Funktion ist nicht definiert an den Stellen und .
Die Funktion soll die maximale Definitionsmenge haben. Da zum Definitionsbereich gehören muss, ist das größte Intervall in dem liegt, das Intervall . Also ist .
Bestimme außerdem die Anzahl der Extremstellen und die Anzahl der Nullstellen der Funktion
Anzahl der Extremstellen
Es gilt: und ist für alle größer null. Damit ist auch für alle größer null, d.h. hat keine Nullstellen es gibt keine Extrema.
Anzahl der Nullstellen
Jede Integralfunktion hat an ihrer unteren Grenze eine Nullstelle.
hat an der Stelle eine Nullstelle. Da für streng monoton steigend ist, gibt es keine weiteren Nullstellen in diesem Intervall, d.h. die Anzahl der Nullstellen ist eins.
2. Berechne den exakten Wert von
Bestimme eine integralfreie Form des Funktionsterms . Löse das Integral zunächst unbestimmt.
Es ist .
Forme umPolynomdivision führt auf:
Bestimme eine Stammfunktion von :
Zerlegung in zwei Integrale:
Wende für das zweite Integral eine Partialbruchzerlegung an:
Koeffizientenvergleich liefert:
und und
Dann erhält man die Stammfunktion:
Es ist
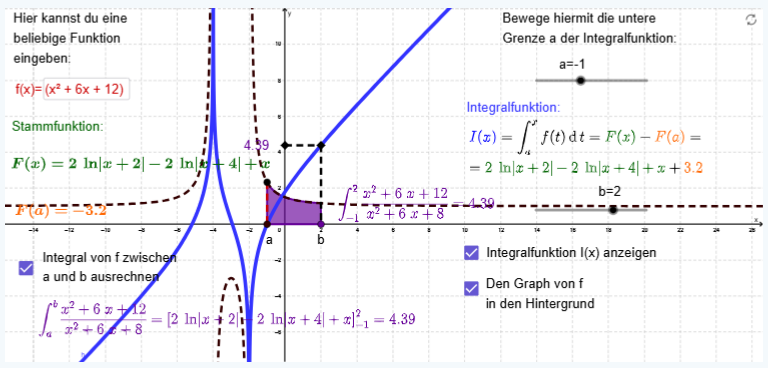
Siehe auch die violett markierte Fläche () in der folgenden Abbildung, die nur zur Veranschaulichung dient.