Berechnen des Volumens des Kegels.

Die Formel zur Berechnung des Volumens eines Kegels lautet:

${\mathrm{V}}_{\mathrm{K}\mathrm{e}\mathrm{g}\mathrm{e}\mathrm{l}}={\displaystyle \frac{1}{3}}\cdot \mathrm{G}\cdot \mathrm{h}\mathrm{G}={\mathrm{r}}^2\cdot \mathrm{\pi }$

Folgende Größen sind bekannt:

$\mathrm{r}=\mathrm{2,5}\text{ cm};\mathrm{h}=5\text{ cm}$

Einsetzen der bekannten Größen in die Formel.

${\mathrm{V}}_{\mathrm{K}\mathrm{e}\mathrm{g}\mathrm{e}\mathrm{l}}={\displaystyle \frac{1}{3}}\cdot {\mathrm{2,5}}^2\cdot \mathrm{\pi }\cdot 5$

${\mathrm{V}}_{\mathrm{K}\mathrm{e}\mathrm{g}\mathrm{e}\mathrm{l}}=\mathrm{32,7}{\text{ cm}}^3$

Das Volumen des Kegels beträgt: ⁣$\mathrm{32,7}{\text{ cm}}^3$.

Berechnen des prozentualen Anteils des Kegelvolumens am Würfelvolumen.

Berechnen des Würfelvolumens.

Die Formel zur Berechnung des Volumens eines Würfels lautet:

${\mathrm{V}}_{\mathrm{W}\ddot{\mathrm{u}}\mathrm{r}\mathrm{f}\mathrm{e}\mathrm{l}}={\mathrm{a}}^3$

Einsetzen der bekannten Größe in die Formel.

${\mathrm{V}}_{\mathrm{W}\ddot{\mathrm{u}}\mathrm{r}\mathrm{f}\mathrm{e}\mathrm{l}}=5^3$

${\mathrm{V}}_{\mathrm{W}\ddot{\mathrm{u}}\mathrm{r}\mathrm{f}\mathrm{e}\mathrm{l}}=125{\text{ cm}}^3$

Das Volumen des Würfels beträgt: $125{\text{ cm}}^3$.

Das Volumen des Kegels beträgt: $\mathrm{32,7}{\text{ cm}}^3$.

Der prozentuale Anteil ist dann:

$\mathrm{p}={\displaystyle \frac{{\mathrm{V}}_{\mathrm{K}\mathrm{e}\mathrm{g}\mathrm{e}\mathrm{l}}}{{\mathrm{V}}_{\mathrm{W}\ddot{\mathrm{u}}\mathrm{r}\mathrm{f}\mathrm{e}\mathrm{l}}}}\cdot 100$

$\mathrm{p}={\displaystyle \frac{\mathrm{32,7}}{125}}\cdot 100$

$\mathrm{p}=\mathrm{0,2616}\cdot 100$

$\mathrm{p}=\mathrm{26,16}\%$

Der prozentuale Anteil des Kegelvolumens am Würfelvolumen

beträgt: ⁣$\mathrm{26,16}\%$.

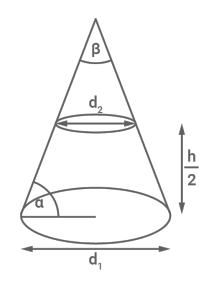
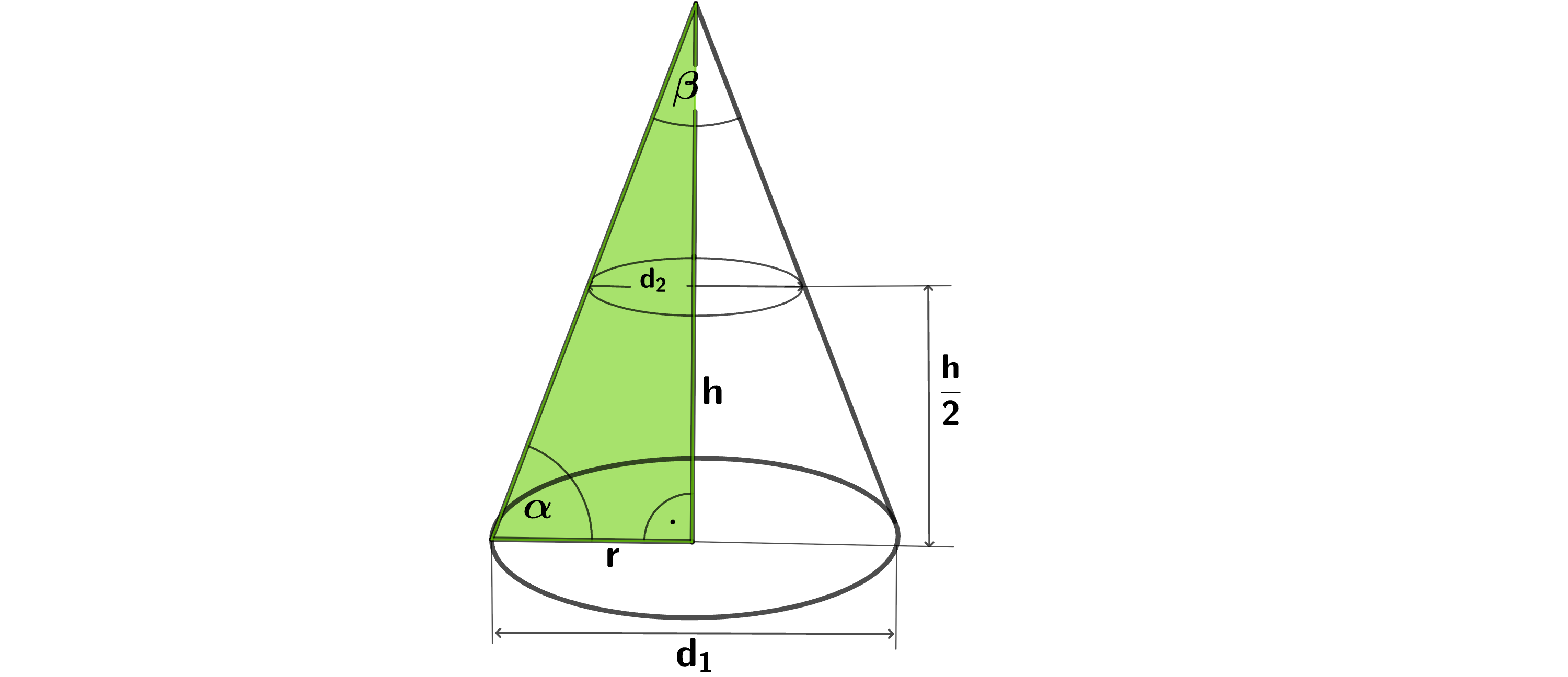
Bestimmen des Winkel $\alpha$ oder $\beta$ des Kegels.

Bestimmen des Winkels $\alpha$ des Kegels.

Das farbig markierte Dreieck ist ein rechtwinkliges Dreieck. Im rechtwinkligem

Dreieck gilt:

${\displaystyle \frac{\mathrm{G}\mathrm{e}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{k}\mathrm{a}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{t}\mathrm{e}}{\mathrm{A}\mathrm{n}\mathrm{k}\mathrm{a}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{t}\mathrm{e}}}=\mathrm{t}\mathrm{a}\mathrm{n}(\mathrm{\alpha })$

In unserem Dreieck gilt dann:

${\displaystyle \frac{\mathrm{h}}{\mathrm{r}}}=\mathrm{t}\mathrm{a}\mathrm{n}(\mathrm{\alpha })$

Einsetzen der bekannten Größen in die Formel.

${\displaystyle \frac{5}{\mathrm{2,5}}}=\mathrm{t}\mathrm{a}\mathrm{n}(\mathrm{\alpha })\Rightarrow \mathrm{t}\mathrm{a}\mathrm{n}(\mathrm{\alpha })=2$

$\mathrm{\alpha }=\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}(2)$

$\mathrm{\alpha }=\mathrm{63,43}°$

Der Winkel $\mathrm{\alpha }$ beträgt: $\mathrm{63,43}°$.

Bestimmen des Winkels $\beta$ des Kegels.

Um den Winkel $\mathrm{\beta }$ bestimmen zu können, muss erst der Winkel ${\displaystyle \frac{\mathrm{\beta }}{2}}$ berechnet werden.

Hier gibt es zwei Lösungsmöglichkeiten:

1. Lösung

In unserem Dreieck gilt dann:

${\displaystyle \frac{\mathrm{r}}{\mathrm{h}}}=\mathrm{t}\mathrm{a}\mathrm{n}\left({\displaystyle \frac{\mathrm{\beta }}{2}}\right)$

Einsetzen der bekannten Größen in die Formel.

${\displaystyle \frac{\mathrm{2,5}}{5}}=\mathrm{t}\mathrm{a}\mathrm{n}\left({\displaystyle \frac{\mathrm{\beta }}{2}}\right)\Rightarrow \mathrm{t}\mathrm{a}\mathrm{n}\left({\displaystyle \frac{\mathrm{\beta }}{2}}\right)=\mathrm{0,5}$

${\displaystyle \frac{\mathrm{\beta }}{2}}=\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}(\mathrm{0,5})$

${\displaystyle \frac{\mathrm{\beta }}{2}}=\mathrm{26,57}°\Rightarrow \mathrm{\beta }=\mathrm{26,57}\cdot 2$

$\mathrm{\beta }=\mathrm{53,14}°$

Der Winkel $\mathrm{\beta }$ beträgt: $\mathrm{53,14}°$.

2. Lösung

Im Dreieck ist die Winkelsumme $180°$. Dann ist ${\displaystyle \frac{\mathrm{\beta }}{2}}=180°-90°-\mathrm{63,43}°=\mathrm{26,57}°$ und $\mathrm{\beta }=\mathrm{26,57}°\cdot 2=\mathrm{53,14}°$. Der Winkel $\mathrm{\beta }$ beträgt: $\mathrm{53,14}°$.

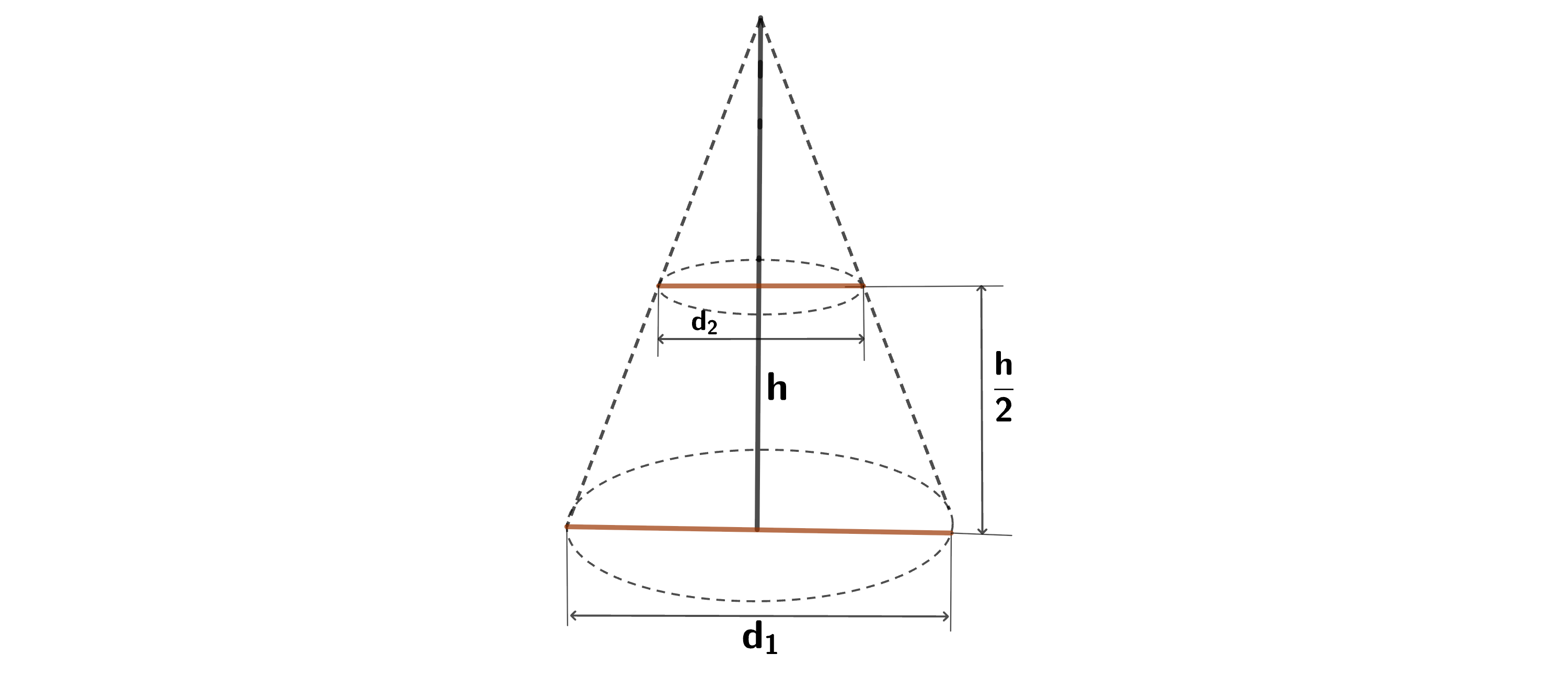
Überprüfen, mithilfe des Strahlensatzes, ob die Aussage richtig ist.

Anwendung des Strahlensatzes auf die Figur in Bild 2.

${\displaystyle \frac{{\mathrm{d}}_1}{{\mathrm{d}}_2}}={\displaystyle \frac{\mathrm{h}}{\left({\displaystyle \frac{\mathrm{h}}{2}}\right)}}{\displaystyle \frac{\mathrm{h}}{\left({\displaystyle \frac{\mathrm{h}}{2}}\right)}}={\displaystyle \frac{2\cdot \cancel{\mathrm{h}}}{\cancel{\mathrm{h}}}}$

${\displaystyle \frac{{\mathrm{d}}_1}{{\mathrm{d}}_2}}=2|\cdot {\mathrm{d}}_2$

${\mathrm{d}}_1=2\cdot {\mathrm{d}}_2|:2\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{S}\mathrm{e}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{n}$

${\mathrm{d}}_2={\displaystyle \frac{{\mathrm{d}}_1}{2}}$

Die Aussage ist richtig.

Erstellen des Baumdiagramms.

Bestimmen der Anzahl der roten, gelben und blauen Kugeln.

Hier handelt es sich um ein Zufallsexperiment ohne zurücklegen, die Zähler der als Brüche angegebenen Wahrscheinlichkeiten sind das Produkt von zwei aufeinanderfolgenden absteigenden natürlichen Zahlen.

Berechnen der Anzahl der roten Kugeln:

${\mathrm{n}}_{\mathrm{r}}\cdot ({\mathrm{n}}_{\mathrm{r}}-1)=20$

${\mathrm{n}}_{\mathrm{r}}^2-{\mathrm{n}}_{\mathrm{r}}-20=0$zerlegen in Linearfaktoren

$({\mathrm{n}}_{\mathrm{r}}-5)({\mathrm{n}}_{\mathrm{r}}+4)=0\Rightarrow {\mathrm{n}}_{\mathrm{r}1}=5;\cancel{{\mathrm{n}}_{\mathrm{r}2}=-4}$

Die Anzahl der roten Kugeln beträgt: $5$

Berechnen der Anzahl der gelben Kugeln:

${\mathrm{n}}_{\mathrm{g}}\cdot ({\mathrm{n}}_{\mathrm{g}}-1)=30$

${\mathrm{n}}_{\mathrm{g}}^2-{\mathrm{n}}_{\mathrm{g}}-30=0$zerlegen in Linearfaktoren

$({\mathrm{n}}_{\mathrm{g}}-6)({\mathrm{n}}_{\mathrm{g}}+5)=0\Rightarrow {\mathrm{n}}_{\mathrm{g}1}=6;\cancel{{\mathrm{n}}_{\mathrm{g}2}=-5}$

Die Anzahl der gelben Kugeln beträgt: $6$

Berechnen der Anzahl der blauen Kugeln:

${\mathrm{n}}_{\mathrm{b}}\cdot ({\mathrm{n}}_{\mathrm{b}}-1)=12$

${\mathrm{n}}_{\mathrm{b}}^2-{\mathrm{n}}_{\mathrm{b}}-12=0$zerlegen in Linearfaktoren

$({\mathrm{n}}_{\mathrm{b}}-4)({\mathrm{n}}_{\mathrm{b}}+3)=0\Rightarrow {\mathrm{n}}_{\mathrm{b}1}=4;\cancel{{\mathrm{n}}_{\mathrm{b}2}=-3}$

Die Anzahl der blauen Kugeln beträgt: $4$

Alternativ kannst Du auch die Anzahl der blauen Kugeln bestimmen, indem Du die folgende Gleichung löst:

$n_r+n_g+n_b=15\Rightarrow 5+6+n_b=15\Rightarrow n_b=15-11=4$

Bestimmen der Wahrscheinlichkeit, dass eine goldene und eine silberne Kugel gezogen werden.

Die Reihenfolge spielt keine Rolle!

${\mathrm{P}}_{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d}/\mathrm{s}\mathrm{i}\mathrm{l}\mathrm{b}\mathrm{e}\mathrm{r}}={\displaystyle \frac{26}{58}}\cdot {\displaystyle \frac{13}{58}}\Rightarrow {\mathrm{P}}_{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d}/\mathrm{s}\mathrm{i}\mathrm{l}\mathrm{b}\mathrm{e}\mathrm{r}}={\displaystyle \frac{338}{3364}}$

${\mathrm{P}}_{\mathrm{s}\mathrm{i}\mathrm{l}\mathrm{b}\mathrm{e}\mathrm{r}/\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d}}={\displaystyle \frac{13}{58}}\cdot {\displaystyle \frac{26}{58}}\Rightarrow {\mathrm{P}}_{\mathrm{s}\mathrm{i}\mathrm{l}\mathrm{b}\mathrm{e}\mathrm{r}/\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d}}={\displaystyle \frac{338}{3364}}$

Damit ist die Wahrscheinlichkeit, dass eine goldene und eine silberne Kugel gezogen werden ${\displaystyle \frac{338}{3364}}\approx \mathrm{0,1}$ oder $10\%$.