Aufgaben zu Integralen - lernen mit Serlo!

🎓 Ui, schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.

Die freie Lernplattform

Was kann man über die $f$ sagen, wenn man weiß:

$\int_{0}^{1} f (x) d x = 0$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Integralrechnung
$\int_{0}^{1} f (x) d x = 0$
Es gibt zwei Möglichkeiten:
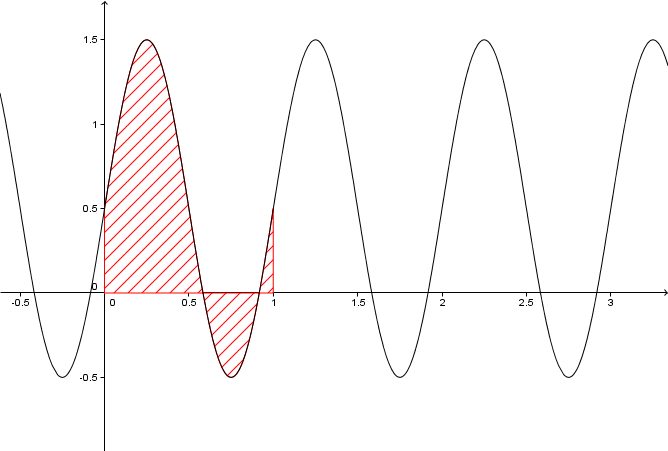
Die Funktion verläuft zwischen 0 und 1 auf der x-Achse.
Die Flächen ober- und unterhalb der x-Achse sind im Bereich 0 bis 1 gleich groß und heben sich so auf.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$\int_{0}^{1} f (x) d x > 0$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integralrechnung
$\int_{0}^{1} f (x) d x > 0$
Die Flächen oberhalb der x-Achse sind im Bereich 0 bis 1 größer als die unterhalb.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$\int_{0}^{1} f (x) d x < 0$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integralrechnung
$\int_{0}^{1} f (x) d x < 0$
Die Flächen unterhalb der x-Achse sind im Bereich 0 bis 1 größer als die oberhalb.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$\int_{1}^{0} f (x) d x > 0$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integralrechnung
$\int_{1}^{0} f (x) dx$ $>$ $0$
$- \int_{0}^{1} f (x) dx$ $>$ $0$ $: (- 1)$
↓
Dividiere durch $(- 1)$ . Dadurch dreht sich das Größer-Zeichen um.
$\int_{0}^{1} f (x) d x$ $<$ $0$
Mögliche Lösung: siehe Teilaufgabe c.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.