Aufgaben zu Integralen

Hier findest du Übungsaufgaben zu den Integralen. Wiederhole wichtige Grundlagen und entdecke interessante Eigenschaften der Integrale!

1
Begründe, warum es kein $\mathrm k\in \mathbb{R}^+$ gibt, das folgende Gleichung erfüllt:
$\displaystyle\int_0^\mathrm k (x^2+1)\ \mathrm{d}x=-1$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integral
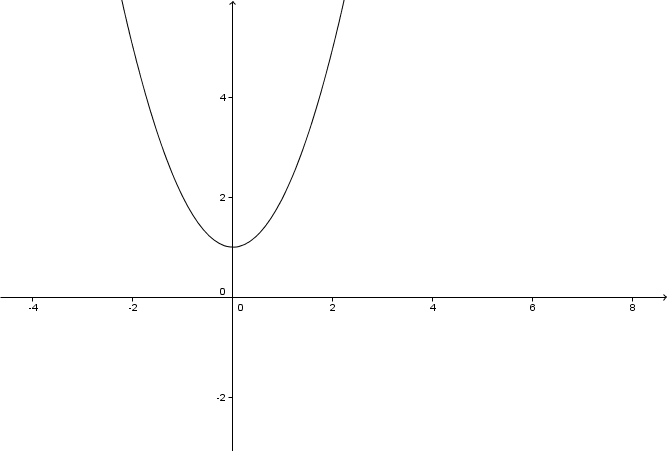
Wir haben hier ein Integral, bei dem die obere Grenze größer als die untere ist. Damit dieses Integral in einem beliebigen Abschnitt negativ wird, muss die Funktion in diesem Bereich einen größeren Flächeninhalt unterhalb der $x$ -Achse haben als oberhalb. Das kann nur geschehen, wenn es negative Funktionswerte gibt.
Da $f(x)=x^2+1$ eine nach oben geöffnete Parabel ist, die sich vollständig oberhalb der $x$ -Achse befindet, sind aber alle Funktionswerte positiv.
2
Berechne die Fläche zwischen der x-Achse und $G_f$ im Bereich von $x= a$ bis $x= b$ .
1. $f(x)=x^3$ $a=0$ $b=1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung
  Im Bereich $x=0$ bis $x=1$ hat die Funktion $f(x)=x^3$ keine Nullstellen, so dass es reicht, das Integral in den angegebenen Grenzen zu berechnen.
  $f(x)=x^3$ , $a=0$ , $b=1$
  Integral aufstellen.
  $\int_0^1x^3\mathrm{d}x=\left[\frac{x^4}4\right]_0^1$
  In die Klammer wird für $x$ der obere Wert (1) eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
  $=\left(\frac{1^4}4\right)-\left(\frac{0^4}4\right)$
  Zähler berechnen.
  $=\frac14$
  Die Fläche zwischen der $x$ -Achse und $G_f$ beträgt $A=\dfrac{1}{4}\; \text{FE}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f(x)=x^3$ $a=1$ $b=2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung
  Im Bereich $x=1$ bis $x=2$ ist die Funktion $f(x)=x^3$ positiv und hat keine Nullstellen, so dass es reicht, das Integral in den angegebenen Grenzen zu berechnen.
  $f(x)=x^3$ , $a=1$ , $b=2$
  Integral aufstellen.
  $\int_1^2 x^3\mathrm{d}x=\left[\frac14x^4\right]_1^2$
  Integrieren.
  In die Klammer wird für $x$ der obere Wert (2) eingesetzt und minus die Klammer mit dem unteren Wert (1) gerechnet.
  $=\frac142^4-\frac141^4$
  Potenzen berechen.
  $=\frac{16}4-\frac14$
  $=\frac{15}4=3{,}75$
  Die Fläche zwischen der x-Achse und $G_f$ beträgt $A=3{,}75\;\text{FE}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $f(x)=-x^2+x$ $a=-1$ $b=0$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung
  Im Bereich $x=-1$ bis $x=0$ hat die Funktion $f(x)=-x^2+x$ nur die Nullstelle $x=0$ .
  Für die linke Integralgrenze gilt: $f(-1)=-2$ . Die gesuchte Fläche liegt somit unterhalb der x-Achse.
  $f(x)=-x^2+x$ , $a=-1$ , $b=0$
  Integral aufstellen und integrieren:
  $\displaystyle\int_{-1}^0-x^2+x\ \mathrm{d}x=\left[-\frac13x^3+\frac12x^2\right]_{-1}^0$
  In die Klammer wird für $x$ der obere Wert (0) eingesetzt und minus die Klammer mit dem unteren Wert (-1) gerechnet.
  $=\left(-\frac{1}{3}\cdot0^3+\frac{1}{2}\cdot0^2\right)-\left(-\frac{1}{3}\cdot\left(-1\right)^3+\frac{1}{2}\cdot\left(-1\right)^2\right)$
  Die erste Klammer ist gleich $"0"$ diese bleibt und auch das Vorzeichen ( - ) vor der zweiten Klammer.
  $=0-\left(\frac{1}{3}+\frac{1}{2}\right)$
  Hauptnenner (6) bilden und beide Brüche auf diesen erweitern.
  $=0-\left(\frac{2}{6}+\frac{3}{6}\right)=-\frac{5}{6}$
  Die Fläche zwischen der x-Achse und $G_f$ beträgt $A=\vert-\frac{5}{6}\vert=\frac{5}{6}\;\text{FE}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Berechne

$\int_0^xt\mathrm{d}t$

$\int_1^xt\mathrm{d}t$

$\int_0^x(t^2-t-1)\mathrm{d}t$

$\int_0^x\sin t\ \mathrm{d}t$

$\int_{1054}^xt^2\ \mathrm{d}t$

$\int_1^2\frac{1+x}x\ \mathrm{d}x$

$\int_1^e\frac{x^2+2x+3}{2x}\ \mathrm{d}x$

$\int_{-2}^{+2}v^2\ \mathrm{d}v$

$\int_2^3t^2\ \mathrm{d}t$

$\int_2^3x^2\ \mathrm{d}x$

$\int_0^1(x-x^2)\ \mathrm{d}x$

$\int_0^2x\ \mathrm{d}x$

$\int_1^3x\ \mathrm{d}x$

$\int_{-2}^0\left(-x\right)\ \mathrm{d}x$

$\int_0^1\left(x^2+x\right)\ \mathrm{d}x$

$\int_1^2x^2\ \mathrm{d}x$

$\int_{-2}^{-1}x^2\ \mathrm{d}x$

$\int_{-2}^2x^2\ \mathrm{d}x$

$\int_0^\frac{\pi}2\sin x\ \mathrm{d}x$

$\int_0^\frac{\pi}2\cos x\ \mathrm{d}x$

$\int_{732}^{2000}1\ \mathrm{d}x$

$\int_1^2(x^2+x)\ \mathrm{d}x$

$\int_0^2(x^2+x)\ \mathrm{d}x$

$\int_{-1}^1\left(5x^4-3x^2-7\right)\ \mathrm{d}x$

Was kann man über die $f$ sagen, wenn man weiß:

$\int_0^1f(x)\mathrm{d}x=0$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Integralrechnung
$\int_0^1f(x)\mathrm{d}x=0$
Es gibt zwei Möglichkeiten:
Die Funktion verläuft zwischen 0 und 1 auf der x-Achse.
Die Flächen ober- und unterhalb der x-Achse sind im Bereich 0 bis 1 gleich groß und heben sich so auf.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$\int_0^1f(x)\mathrm{d}x>0$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integralrechnung
$\int_0^1f(x)\mathrm{d }x>0$
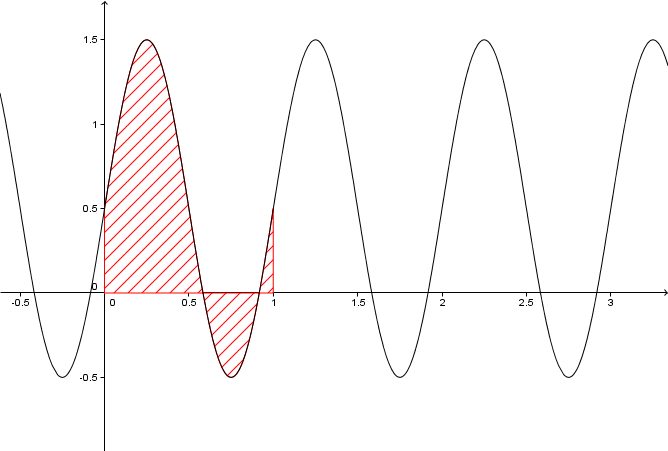
Die Flächen oberhalb der x-Achse sind im Bereich 0 bis 1 größer als die unterhalb.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$\int_0^1f(x)\mathrm{d}x<0$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integralrechnung
$\int_0^1f(x)\mathrm{d}x<0$
Die Flächen unterhalb der x-Achse sind im Bereich 0 bis 1 größer als die oberhalb.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$\int_1^0f(x)\mathrm{d}x>0$

Berechne die Integrale: $a(x)=6-\frac{1}{24}x^2\ ;\ D_a=\mathbb{R}$

$\int_0^{12}a(x)\mathrm{d}x$

$\int_{-12}^{12}a(x)\mathrm{d}x$

$\int_0^{12\sqrt3}a(x)\mathrm{d}x$

Berechne.

$\int_{-1}^1e^{\left|x\right|}\ \mathrm{d}x$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrieren

$\int_{-1}^1e^{\left|x\right|}\ \mathrm{d}x$

Fallunterscheidung für $x\geq0$ und $x<0$

Für $x\geq0$ ist der Betrag immer positiv und kann weggelassen werden.

Für $x<0$ muss der Betrag durch ein Minuszeichen vor $x$ ersetzt werden, da $-x$ für negatives $x$ positiv wird.

Fall $x\geq0$

$\displaystyle \int_0^1e^x\ \mathrm{d}x$	$=$
	↓	Integrieren.
	$=$	$\displaystyle \left[e^x\right]_0^1$
	↓	In die Klammer wird für $x$ der obere Wert $1$ eingesetzt und minus die Klammer mit dem unteren Wert $0$ gerechnet.
	$=$	$\displaystyle e^1-e^0$
	$=$	$\displaystyle e-1$

Fall $x<0$

$\displaystyle \int_{-1}^0e^{-x}\ \mathrm{d}x$	$=$
	↓	Integrieren.
	$=$	$\displaystyle \left[-e^{-x}\right]_{-1}^0$
	↓	In die Klammer wird für $x$ der obere Wert $0$ eingesetzt und minus die Klammer mit dem unteren Wert $(-1)$ gerechnet.
	$=$	$\displaystyle \left(-e^{-0}\right)-\left(-e^{-\left(-1\right)}\right)$
	↓	Klammern auflösen.
	$=$	$\displaystyle -e^0+e^1$
	$=$	$\displaystyle -1+e$

Gesamtfläche berechnen

$\displaystyle A$	$=$	$\displaystyle \left(e-1\right)+\left(-1+e\right)$
	↓	Klammern auflösen.
	$=$	$\displaystyle e-1-1+e$
	$=$	$\displaystyle 2e-2$

Alternative Lösung

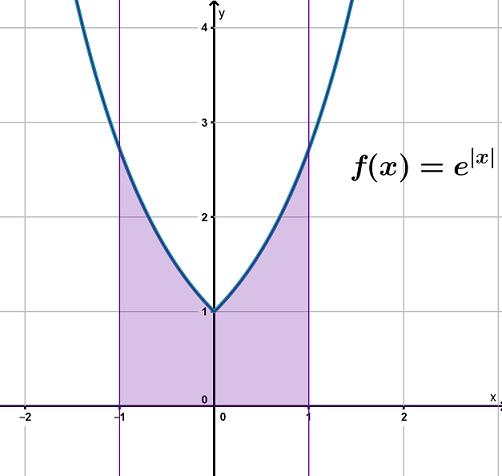
Graph Funktion achsensymmetrisch Integration

Du kannst hier ausnutzen, dass die Funktion achsensymmetrisch ist. Damit ist der Flächeninhalt, der zwischen $-1$ und $0$ eingeschlossen ist, genauso groß wie der Flächeninhalt, der zwischen $0$ und $1$ eingeschlossen ist (siehe Abbildung rechts).

$\Rightarrow$ $\int_{-1}^1e^{\left|x\right|}\ \mathrm{d}x=2 \cdot \int_0^1e^x\ \mathrm{d}x$

Gleiche Rechnung wie oben.

$=2\cdot\left[e^x\right]_0^1=2\cdot[e^1-e^0]$ $=2\cdot(e-1)=\ 2e-2$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$\int_{-2}^0e^{-\left|x\right|}\ \mathrm{d}x$

$\int_{-2}^0e^{\left|x+1\right|}\ \mathrm{d}x$

$\int_{-7}^7\frac{\left|t\right|}te^{\left|t\right|}\ \mathrm{d}t$

Stelle $f(x)$ integralfrei dar.

$f(x)=\int_0^x\sqrt t\ \mathrm{d}t$

$f(x)=x\cdot\ln x+\int_2^x\ln t\;\ \mathrm{d}t$

$f(x)=\ln x-\int_1^x\frac1t\ \mathrm{d}t$

$f(x)=\int_1^xt\;\ln t\ \mathrm{d}t+\int_x^3t\;\ln t\ \mathrm{d}t$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integriere

$f(x)=\int_1^xt\;\ln t\ \mathrm{d}t+\int_x^3t\;\ln t\ \mathrm{d}t$

Da die linke Grenze des ersten Integrals und die rechte des zweiten das gleiche sind und es sich beide male um dieselbe Funktion handelt, kann man die beiden Integrale zusammenfassen.

$=\int_1^3t\;\mathrm{lnt}\ \mathrm{d}t$

Es muss partiell Integriert werden. $t$ wird als $u'$ gewählt, da es sich einfacher integrieren lässt.

$u=\frac12t^2$	$u'=t$
$v=\ln t$	$v'=\frac1t$

$\displaystyle f\left(x\right)$	$=$	$\displaystyle \left[\frac{1}{2}t^2\cdot\ln t\right]_1^3-\int_1^3\left(\frac{1}{2}t^2\cdot\frac{1}{t}\right)\ \mathrm{d}t$
	↓	Im Integral kürzt sich ein $t$ .
	$=$	$\displaystyle \left[\frac{1}{2}t^2\cdot\ln t\right]_1^3-\int_1^3\left(\frac{1}{2}t\right)\ \mathrm{d}t$
	↓	Integrieren.
	$=$	$\displaystyle \left[\frac{1}{2}t^2\cdot\ln t\right]_1^3-\left[\frac{1}{4}t^2\right]_1^3$
	↓	In die Klammer wird für $t$ der obere Wert (3) eingesetzt und minus die Klammer mit dem unteren Wert (1) gerechnet.
	$=$	$\displaystyle \frac{1}{2}\cdot3^2\cdot\ln3-\frac{1}{2}\cdot1^2\cdot\ln1-\frac{1}{4}\cdot3^2+\frac{1}{4}\cdot1^2$
	↓	Ausmultiplizieren.
	$=$	$\displaystyle \frac{9}{2}\cdot\ln3-\frac{1}{2}\cdot\ln1-\frac{9}{4}+\frac{1}{4}$
	$=$	$\displaystyle \frac{9}{2}\cdot\ln3-\frac{1}{2}\cdot\ln1-2$
	$≈$	$\displaystyle 2{,}944$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

8
Löse die Aufgabe (nach einer Abituraufgabe von 2012)
1. Begründe, dass jede Integralfunktion mindestens eine Nullstelle hat.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: integrale
  Für Integrale gilt: $\displaystyle \int_a^a f(x)\operatorname{d}x =0$ .
  Daher hat jede Integralfunktion $\displaystyle F(x)=\int_a^x f(x)\operatorname{d}x$ die Nullstelle $x=a$ und damit mindestens eine Nullstelle.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Gib einen Term für eine Funktion $f$ an, sodass die Integralfunktion
  $\displaystyle F: x \mapsto \int_{1}^x f(t)\operatorname{d}t$ unendlich viele Nullstellen hat.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: integrale
  Lösung 1: Für unendlich viele Nullstellen muss die Fläche unter dem Funktionsgraphen immer wechselnd unter und über der x-Achse liegen. Für eine solche Funktion bietet sich der $\sin(x)$ an. Aufgrund der Periodizität des Sinus ist dann für alle $2\pi k,\, k=1;2;3;\ldots$ die Integralfunktion null.
  Lösung 2: Eine einfache Lösung gibt es für $f=0$ . Dann folgt nämlich, dass die Integralfunktion $F$ ebenfalls konstant gleich Null ist. Insbesondere hat $F$ in diesem Fall unendlich viele Nullstellen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Die Funktion $v(t)=-15t^2+90t$ gibt zu jedem Zeitpunkt die momentane Geschwindigkeit eines Autos in $\dfrac{\text{km}}{\text{h}}$ während einer sechsstündigen Autofahrt an.

Welche durchschnittliche Geschwindigkeit hatte das Auto bei seiner Fahrt?

Gegeben ist die Funktion $f(x)=-2x^2+4x$ .

Berechne die Sekantensteigung im Intervall $[0;1]$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung von Funktionen
Es ist $f(x)=-2x^2+4x$ .
Sekantensteigung allgemein:
$m_S=\dfrac{f(b)-f(a)}{b-a}$
Hier folgt:
$m_S=\dfrac{f(1)-f(0)}{1-0}=\dfrac{2-0}{1}=2$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $m_S=\dfrac{f(b)-f(a)}{b-a}$ .

Berechne mithilfe der Integralrechnung die mittlere Steigung im Intervall $[0;1]$ .

Vergleiche mit dem Ergebnis aus Aufgabe a).

Nachdem ein Heißluftballon zur Zeit $t=0$ seine Reisehöhe erreicht hat, wird seine Flughöhe durch die Funktion $h(t)=-0{,}03t^3+0{,}4t^2+300$ beschrieben ( $h$ in Metern und $t$ in Stunden).

Welche durchschnittliche Reisehöhe hatte der Ballon zwischen der $2.$ und $10.$ Stunde?

Eine Wetterstation misst die Lufttemperatur. Der Temperaturverlauf während eines Tages wird näherungsweise durch die Funktion $t(x)=-0{,}01x^3+0{,}25x^2+6$ beschrieben ( $x$ ist die Uhrzeit in Stunden und $t(x)$ die Temperatur in $^\circ$ C).

Wie groß ist die mittlere Tagestemperatur?

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \int_0^xt\mathrm{d}t$	$=$	$\displaystyle \left[\frac{1}{2}t^2\right]_0^x$
	↓	In die Klammer wird für $t$ der obere Wert $(x)$ eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle \frac{1}{2}x^2-\frac{1}{2}0^2$
	$=$	$\displaystyle \frac{1}{2}x^2$

$\displaystyle \int_1^xt\mathrm{d}t$	$=$	$\displaystyle \left[\frac{1}{2}t^2\right]_1^x$
	↓	In die Klammer wird für $t$ der obere Wert $(x)$ eingesetzt und minus die Klammer mit dem unteren Wert (1) gerechnet.
	$=$	$\displaystyle \frac{1}{2}x^2-\frac{1}{2}\cdot1$
	$=$	$\displaystyle \frac{1}{2}x^2-\frac{1}{2}$

$\displaystyle \int_0^x(t^2-t-1)\mathrm{d}t$	$=$	$\displaystyle \left[\frac{1}{3}t^3-\frac{1}{2}t^2-t\right]_0^x$
	↓	In die Klammer wird für $t$ der obere Wert $(x)$ eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle \left(\frac{1}{3}x^3-\frac{1}{2}x^2-x\right)-\left(\frac{1}{3}0^3-\frac{1}{2}0^2-0\right)$
	$=$	$\displaystyle \frac{1}{3}x^3-\frac{1}{2}x^2-x$

$\displaystyle \int_0^x\sin t\ \mathrm{d}t$	$=$	$\displaystyle [-\cos t]_0^x$
	↓	In die Klammer wird für $t$ der obere Wert $(x)$ eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle \left(-\cos x\right)-\left(-\cos0\right)$
	↓	$\cos 0 =1$
	$=$	$\displaystyle -\cos x+1$

$\displaystyle \int_{1054}^xt^2\ \mathrm{d}t$	$=$	$\displaystyle \left[\frac{1}{3}t^3\right]_{1054}^x$
	↓	In die Klammer wird für $t$ der rechte Wert $(x)$ eingesetzt und minus die Klammer mit dem linken Wert (1054) gerechnet.
	$=$	$\displaystyle \left(\frac{1}{3}\cdot x^3\right)-\left(\frac{1}{3}\cdot1054^3\right)$
	$=$	$\displaystyle \frac{1}{3}\cdot x^3-\frac{1054^3}{3}$
	$=$	$\displaystyle \frac{1}{3}\cdot x^3-\frac{1.170.905.464}{3}$

$\displaystyle \int_1^2\frac{1+x}{x}\ \mathrm{d}x$	$=$	$\displaystyle \int_1^2\left(\frac{1}{x}+\frac{x}{x}\right)\ \mathrm{d}x$
	↓	Bruch mit $x$ kürzen.
	$=$	$\displaystyle \int_1^2\left(\frac{1}{x}+1\right)\ \mathrm{d}x$
	↓	Integrieren. Die Stammfunktion von $\frac1x$ ist $\ln x$ .
	$=$	$\displaystyle \left[\ln x+x\right]_1^2$
	↓	In die Klammer wird für $x$ der obere Wert 2 eingesetzt und minus die Klammer mit dem unteren Wert 1 gerechnet.
	$=$	$\displaystyle \left(\ln2+2\right)-\left(\ln1+1\right)$
	↓	$\ln1=0$
	$=$	$\displaystyle \ln2+2-1$
	$=$	$\displaystyle \ln2+1$
	$≈$	$\displaystyle 1{,}6931$

$\displaystyle \int_1^e\frac{x^2+2x+3}{2x}\ \mathrm{d}x$	$=$	$\displaystyle \int_1^e\left(\frac{x^2}{2x}+\frac{2x}{2x}+\frac{3}{2x}\right)\ \mathrm{d}x$
	$=$	$\displaystyle \int_1^e\left(\frac{1}{2}x+1+\frac{3}{2}\cdot\frac{1}{x}\right)\ \mathrm{d}x$
	↓	Integriere. Die Stammfunktion von $\frac1x$ ist $\ln x$ .
	$=$	$\displaystyle \left[\frac{1}{2\cdot2}x^2+x+\frac{3}{2}\ln x\right]_1^e$
	↓	In die Klammer wird für $x$ der obere Wert $(e)$ eingesetzt und minus die Klammer mit dem unteren Wert 1 gerechnet.
	$=$	$\displaystyle \left(\frac{1}{4}e^2+e+\frac{3}{2}\ln e\right)-\left(\frac{1}{4}1^2+1+\frac{3}{2}\ln1\right)$
	↓	Löse die Klammern auf. Dabei ist $\ln e=1$ und $\ln1=0$ .
	$=$	$\displaystyle \frac{e^2}{4}+e+\frac{3}{2}-\frac{1}{4}-1$
	↓	Gleiche Elemente zusammenfassen.
	$=$	$\displaystyle \frac{e^2}{4}+e+\frac{1}{4}$
	$≈$	$\displaystyle 4{,}8155$

$\displaystyle \int_{-2}^{+2}v^2\ \mathrm{d}v$	$=$	$\displaystyle \left[\frac{1}{3}\cdot v^3\right]_{-2}^{+2}$
	↓	In die Klammer wird für $v$ der obere Wert (+2) eingesetzt und minus die Klammer mit dem unteren Wert (-2) gerechnet.
	$=$	$\displaystyle \left(\frac{1}{3}\cdot2^3\right)-\left(\frac{1}{3}\cdot\left(-2\right)^3\right)$
	↓	Klammern auflösen und Potenzen ausmultiplizieren.
	$=$	$\displaystyle \frac{8}{3}+\frac{8}{3}$
	↓	Brüche addieren.
	$=$	$\displaystyle \frac{16}{3}$

$\displaystyle \int_2^3t^2\ \mathrm{d}t$	$=$	$\displaystyle \left[\frac{1}{3}t^3\right]_2^3$
	↓	In die Klammer wird für $t$ der obere Wert (3) eingesetzt und minus die Klammer mit dem unteren Wert (2) gerechnet.
	$=$	$\displaystyle \left(\frac{1}{3}\cdot3^3\right)-\left(\frac{1}{3}\cdot2^3\right)$
	↓	Klammern auflösen.
	$=$	$\displaystyle \frac{27}{3}-\frac{8}{3}$
	↓	Brüche subtrahieren.
	$=$	$\displaystyle \frac{19}{3}$

$\displaystyle \int_2^3x^2\ \mathrm{d}x$	$=$	$\displaystyle \left[\frac{1}{3}x^3\right]_2^3$
	↓	In die Klammer wird für $x$ der obere Wert (3) eingesetzt und minus die Klammer mit dem unteren Wert (2) gerechnet.
	$=$	$\displaystyle \left(\frac{1}{3}\cdot3^3\right)-\left(\frac{1}{3}\cdot2^3\right)$
	↓	Klammern auflösen.
	$=$	$\displaystyle \frac{27}{3}-\frac{8}{3}$
	↓	Brüche subtrahieren.
	$=$	$\displaystyle \frac{19}{3}$

$\displaystyle \int_0^1(x-x^2)\ \mathrm{d}x$	$=$	$\displaystyle \left[\frac{1}{2}x^2-\frac{1}{3}x^3\right]_0^1$
	↓	In die Klammer wird für $x$ der obere Wert (1) eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle \left(\frac{1}{2}\cdot1^2-\frac{1}{3}\cdot1^3\right)-\left(\frac{1}{2}\cdot0^2-\frac{1}{3}\cdot0^3\right)$
	↓	Klammern auflösen, die zweite Klammer fällt weg.
	$=$	$\displaystyle \frac{1}{2}-\frac{1}{3}$
	↓	Brüche subtrahieren.
	$=$	$\displaystyle \frac{3}{6}-\frac{2}{6}$
	$=$	$\displaystyle \frac{1}{6}$

$\displaystyle \int_0^2x\ \mathrm{d}x$	$=$	$\displaystyle \left[\frac{x^2}{2}\right]_0^2$
	↓	In die Klammer wird für $x$ der obere Wert (2) eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle \frac{2^2}{2}-\frac{0^2}{2}$
	$=$	$\displaystyle \frac{4}{2}-0$
	$=$	$\displaystyle 2$

$\displaystyle \int_1^3x\ \mathrm{d}x$	$=$	$\displaystyle \left[\frac{x^2}{2}\right]_1^3$
	↓	In die Klammer wird für $x$ der obere Wert (3) eingesetzt und minus die Klammer mit dem unteren Wert (1) gerechnet.
	$=$	$\displaystyle \frac{3^2}{2}-\frac{1^2}{2}$
	↓	Zähler berechnen.
	$=$	$\displaystyle \frac{9}{2}-\frac{1}{2}$
	$=$	$\displaystyle \frac{8}{2}$
	$=$	$\displaystyle 4$

$\displaystyle \int_{-2}^0\left(-x\right)\ \mathrm{d}x$	$=$	$\displaystyle \left[-\frac{x^2}{2}\right]_{-2}^0$
	↓	In die Klammer wird für $x$ der obere Wert (0) eingesetzt und minus die Klammer mit dem unteren Wert (-2) gerechnet.
	$=$	$\displaystyle \left(-\frac{0^2}{2}\right)-\left(-\frac{(-2)^2}{2}\right)$
	$=$	$\displaystyle \frac{4}{2}$
	$=$	$\displaystyle 2$

$\displaystyle \int_0^1\left(x^2+x\right)\ \mathrm{d}x$	$=$	$\displaystyle \left[\frac{x^3}{3}+\frac{x^2}{2}\right]_0^1$
	↓	In die Klammer wird für $x$ der obere Wert (1) eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle \left(\frac{1^3}{3}+\frac{1^2}{2}\right)-\left(\frac{0^3}{3}+\frac{0^2}{2}\right)$
	$=$	$\displaystyle \frac{1}{3}+\frac{1}{2}$
	↓	Hauptnenner (6) bilden und auf diesen erweitern.
	$=$	$\displaystyle \frac{2}{6}+\frac{3}{6}$
	$=$	$\displaystyle \frac{5}{6}$

$\displaystyle \int_1^0f(x)\mathrm{dx}$	$>$	$\displaystyle 0$
$\displaystyle -\int_0^1f(x)\mathrm{dx}$	$>$	$\displaystyle 0$	$\displaystyle :\left(-1\right)$
	↓	Dividiere durch $(-1)$ . Dadurch dreht sich das Größer-Zeichen um.
$\displaystyle \int_0^1f(x)\mathrm{d}x$	$<$	$\displaystyle 0$

$\displaystyle \int_1^2x^2\ \mathrm{d}x$	$=$	$\displaystyle \left[\frac{1}{3}x^3\right]_1^2$
	↓	In die Klammer wird für $x$ der obere Wert (2) eingesetzt und minus die Klammer mit dem unteren Wert (1) gerechnet.
	$=$	$\displaystyle \frac{1}{3}\cdot2^3-\frac{1}{3}\cdot1^3$
	$=$	$\displaystyle \frac{8}{3}-\frac{1}{3}$
	$=$	$\displaystyle \frac{7}{3}$

$\displaystyle \int_{-2}^{-1}x^2\ \mathrm{d}x$	$=$	$\displaystyle \left[\frac{1}{3}x^3\right]_{-2}^{-1}$
	↓	In die Klammer wird für $x$ der obere Wert (-1) eingesetzt und minus die Klammer mit dem unteren Wert (-2) gerechnet.
	$=$	$\displaystyle \frac{1}{3}\cdot\left(-1\right)^3-\frac{1}{3}\cdot\left(-2\right)^3$
	↓	Potenzen berechen.
	$=$	$\displaystyle -\frac{1}{3}+\frac{8}{3}$
	$=$	$\displaystyle \frac{7}{3}$

$\displaystyle \int_{-2}^2x^2\ \mathrm{d}x$	$=$	$\displaystyle \left[\frac{1}{3}x^3\right]_{-2}^2$
	↓	In die Klammer wird für $x$ der obere Wert (2) eingesetzt und minus die Klammer mit dem unteren Wert (-2) gerechnet.
	$=$	$\displaystyle \frac{1}{3}\cdot2^3-\frac{1}{3}\cdot\left(-2\right)^3$
	↓	Potenzen berechen.
	$=$	$\displaystyle \frac{8}{3}+\frac{8}{3}$
	$=$	$\displaystyle \frac{16}{3}$

$\displaystyle \int_0^{\frac{\pi}{2}}\sin x\ \mathrm{d}x$	$=$	$\displaystyle \left[-\cos x\right]_0^{\frac{\mathrm{\pi}}{2}}$
	↓	In die Klammer wird für x der rechte Wert $\left(\frac{\mathrm\pi}2\right)$ eingesetzt und minus die Klammer mit dem linken Wert (0) gerechnet.
	$=$	$\displaystyle -\cos\frac{\mathrm{\pi}}{2}+\cos0$
	↓	Kosinus im Bogenmaß berechnen.
	$=$	$\displaystyle 0+1$
	$=$	$\displaystyle 1$

$\displaystyle \int_0^{\frac{\pi}{2}}\cos x\ \mathrm{d}x$	$=$	$\displaystyle \left[\sin x\right]_0^{\frac{\mathrm{\pi}}{2}}$
	↓	In die Klammer wird für $x$ der obere Wert $\left(\frac{\pi}{2}\right)$ eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle \sin\frac{\mathrm{\pi}}{2}-\sin0$
	↓	Kosinus im Bogenmaß berechnen.
	$=$	$\displaystyle 1+0$
	$=$	$\displaystyle 1$

$\displaystyle \int_{732}^{2000}1\mathrm{dx}$	$=$	$\displaystyle \left[x\right]_{732}^{2000}$
	↓	In die Klammer wird für $x$ der obere Wert (2000) eingesetzt und minus die Klammer mit dem unteren Wert (732) gerechnet.
	$=$	$\displaystyle 2000-732$
	$=$	$\displaystyle 1268$

$\displaystyle \int_1^2(x^2+x)\ \mathrm{d}x$	$=$	$\displaystyle \left[\frac{1}{3}x^3+\frac{1}{2}x^2\right]_1^2$
	↓	In die Klammer wird für $x$ der obere Wert (2) eingesetzt und minus die Klammer mit dem unteren Wert (1) gerechnet.
	$=$	$\displaystyle \left(\frac{1}{3}\cdot2^3+\frac{1}{2}\cdot2^2\right)-\left(\frac{1}{3}\cdot1^3+\frac{1}{2}\cdot1^2\right)$
	$=$	$\displaystyle \frac{8}{3}+\frac{4}{2}-\left(\frac{1}{3}+\frac{1}{2}\right)$
	↓	Hauptnenner bilden.
	$=$	$\displaystyle \frac{8}{3}+\frac{6}{3}-\left(\frac{2}{6}+\frac{3}{6}\right)$
	$=$	$\displaystyle \frac{14}{3}-\frac{5}{6}$
	↓	Hauptnenner bilden.
	$=$	$\displaystyle \frac{28}{6}-\frac{5}{6}$
	$=$	$\displaystyle \frac{23}{6}$

$\displaystyle \int_0^2(x^2+x)\ \mathrm{d}x$	$=$	$\displaystyle \left[\frac{1}{3}x^3+\frac{1}{2}x^2\right]_0^2$
	↓	In die Klammer wird für $x$ der obere Wert (2) eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet
	$=$	$\displaystyle \left(\frac{1}{3}\cdot2^3+\frac{1}{2}\cdot2^2\right)-\left(\frac{1}{3}\cdot0^3+\frac{1}{2}\cdot0^2\right)$
	$=$	$\displaystyle \frac{8}{3}+\frac{4}{2}$
	↓	Hauptnenner bilden.
	$=$	$\displaystyle \frac{16}{6}+\frac{12}{6}$
	$=$	$\displaystyle \frac{28}{6}$
	$=$	$\displaystyle \frac{14}{3}$

$\displaystyle \int_{-1}^1\left(5x^4-3x^2-7\right)\ \mathrm{d}x$	$=$	$\displaystyle \left[x^5-x^3-7x\right]_{-1}^1$
	$=$	$\displaystyle \left[1^5-1^3-7\cdot1-\left(\left(-1\right)^5-\left(-1\right)^3-7\cdot\left(-1\right)\right)\right]$
	$=$	$\displaystyle 1-1-7-\left(-1-\left(-1\right)+7\right)$
	$=$	$\displaystyle -7-\left(-1+1+7\right)$
	$=$	$\displaystyle -7-7$
	$=$	$\displaystyle -14$

$\displaystyle \int_{-1}^1\left(5x^4-3x^2-7\right)\ \mathrm{d}x$	$=$	$\displaystyle 2\cdot\int_0^1\left(5x^4-3x^2-7\right)\ \mathrm{d}x$
	$=$	$\displaystyle 2\cdot\left[x^5-x^3-7x\right]_0^1$
	↓	0 und 1 einsetzen
	$=$	$\displaystyle 2\cdot\left[1^5-1^3-7\cdot1-\left(0^5-0^3-7\cdot0\right)\right]$
	$=$	$\displaystyle 2\cdot\left(1-1-7-0\right)$
	$=$	$\displaystyle 2\cdot(-7)$
	$=$	$\displaystyle -14$

Aufgaben zu Integralen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Alternative Lösung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Fall x≥0x\geq0x≥0

Fall x<0x<0x<0

Gesamtfläche berechnen

Alternative Lösung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Fall x≥−1x\geq-1x≥−1

Fall x<−1x<-1x<−1

Gesamtfläche berechnen

Hast du eine Frage oder Feedback?

Fall t≥0t\geq0t≥0

Fall t<0t< 0t<0

Gesamtfläche berechnen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Vergleiche mit dem Ergebnis aus Aufgabe a).

Hast du eine Frage oder Feedback?

Fall $x\geq0$

Fall $x<0$

Fall $x\geq-1$

Fall $x<-1$

Fall $t\geq0$

Fall $t< 0$

$\displaystyle \int_0^{12}6-\frac{1}{24}x^2dx$	$=$
	↓	Integrieren.
	$=$	$\displaystyle \left[6x-\frac{1}{24\cdot3}x^3\right]_0^{12}$
	↓	In die Klammer wird für $x$ der obere Wert (12) eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle \left(6\cdot12-\frac{1}{72}\cdot12^3\right)-\left(6\cdot0-\frac{1}{72}\cdot0^3\right)$
	↓	Klammern auflösen, die zweite Klammer fällt weg.
	$=$	$\displaystyle 72-\frac{1728}{72}$
	↓	Der Bruch lässt sich mit 72 kürzen.
	$=$	$\displaystyle 72-24$
	$=$	$\displaystyle 48$

$\displaystyle \int_{-12}^{12}6-\frac{1}{24}x^2\ \mathrm{d}x$	$=$
	↓	Integrieren.
	$=$	$\displaystyle \left[6x-\frac{1}{24\cdot3}x^3\right]_{-12}^{12}$
	↓	In die Klammer wird für $x$ der obere Wert (12) eingesetzt und minus die Klammer mit dem unteren Wert (-12) gerechnet.
	$=$	$\displaystyle \left(6\cdot12-\frac{1}{72}\cdot12^3\right)-\left(6\cdot\left(-12\right)-\frac{1}{72}\cdot\left(-12\right)^3\right)$
	↓	Klammer auflösen.
	$=$	$\displaystyle 72-\frac{1728}{72}+72-\frac{1728}{72}$
	↓	Die Brüche mit 72 kürzen .
	$=$	$\displaystyle 72-24+72-24$
	$=$	$\displaystyle 96$

$\displaystyle \int_0^{12\sqrt{3}}6-\frac{1}{24}x^2\ \mathrm{d}x$	$=$
	↓	Integrieren.
	$=$	$\displaystyle \left[6x-\frac{1}{24\cdot3}x^3\right]_0^{12\sqrt{3}}$
	↓	In die Klammer wird für $x$ der obere Wert ( $12\sqrt 3$ ) eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle \left(6\cdot12\cdot\sqrt{3}-\frac{\left(12\cdot\sqrt{3}\right)^3}{72}\right)-\left(6\cdot0-\frac{1}{72}\cdot0\right)$
	↓	Klammern auflösen, die zweite Klammer fällt weg.
	$=$	$\displaystyle 72\cdot\sqrt{3}-\frac{5184\cdot\sqrt{3}}{72}$
	↓	Der Bruch lässt sich mit 72 kürzen .
	$=$	$\displaystyle 72\cdot\sqrt3-{\textstyle72}{\textstyle\cdot}{\textstyle\sqrt3}=0$

$\displaystyle \int_{-2}^0e^{-\left\|x\right\|}\ \mathrm{d}x$	$=$
	↓	Da $x$ immer negativ ( bzw. 0 ) ist, kann der Betrag durch ein minus ersetzt werden.
	$=$	$\displaystyle \int_{-2}^0e^{-\left(-x\right)}\ \mathrm{d}x$
	$=$	$\displaystyle \int_{-2}^0e^x\ \mathrm{d}x$
	↓	Integrieren.
	$=$	$\displaystyle \left[e^x\right]_{-2}^0$
	↓	In die Klammer wird für $x$ der obere Wert 0 eingesetzt und minus die Klammer mit dem unteren Wert (-2) gerechnet.
	$=$	$\displaystyle e^0-e^{-2}$
	$=$	$\displaystyle 1-\frac{1}{e^2}$
	$≈$	$\displaystyle 0{,}86467$

$\displaystyle \int_{-1}^0e^{x+1}\ \mathrm{d}x$	$=$
	↓	Integrieren.
	$=$	$\displaystyle \left[e^{x+1}\right]_{-1}^0$
	↓	In die Klammer wird für $x$ der obere Wert $0$ eingesetzt und minus die Klammer mit dem unteren Wert $-1$ gerechnet.
	$=$	$\displaystyle e^1-e^0$
	$=$	$\displaystyle e-1$

$\displaystyle \int_{-2}^{-1}e^{-\left(x+1\right)}\ \mathrm{d}x$	$=$
	↓	Klammern auflösen.
	$=$	$\displaystyle \int_{-2}^{-1}e^{-x-1}\ \mathrm{d}x$
	↓	Integrieren.
	$=$	$\displaystyle \left[-e^{-x-1}\right]_{-2}^{-1}$
	↓	In die Klammer wird für $x$ der obere Wert $-1$ eingesetzt und minus die Klammer mit dem unteren Wert $-2$ gerechnet.
	$=$	$\displaystyle (-e^{-(-1)-1})-(-e^{-(-2)-1})$
	↓	Klammern auflösen.
	$=$	$\displaystyle -e^0+e^1$
	$=$	$\displaystyle -1+e$

$\displaystyle \int_0^7\frac{t}{t}e^t\ \mathrm{d}t$	$=$
	↓	Mit t kürzen.
	$=$	$\displaystyle \int_0^7e^t\ \mathrm{d}t$
	↓	Integrieren.
	$=$	$\displaystyle \left[e^t\right]_0^7$
	↓	In die Klammer wird für tt der obere Wert (7) eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle e^7-e^0$
	$=$	$\displaystyle e^7-1$

$\displaystyle \int_{-7}^0\frac{-t}{t}e^{-t}\ \mathrm{d}t$	$=$
	↓	Mit t kürzen.
	$=$	$\displaystyle \int_{-7}^0-e^{-t}\ \mathrm{d}t$
	↓	Integrieren.
	$=$	$\displaystyle \left[e^{-t}\right]_{-7}^0$
	↓	In die Klammer wird für $t$ der obere Wert (0) eingesetzt und minus die Klammer mit dem unteren Wert (-7) gerechnet.
	$=$	$\displaystyle e^0-e^{-\left(-7\right)}$
	$=$	$\displaystyle 1-e^7$

$\displaystyle A$	$=$	$\displaystyle \left(e^7-1\right)+\left(1-e^7\right)$
	$=$	$\displaystyle e^7-1+1-e^7$
	$=$	$\displaystyle 0$

$\displaystyle f\left(x\right)$	$=$	$\displaystyle \int_0^x\sqrt{t}\ \mathrm{d}t$
	↓	Wurzel als Potenz schreiben.
	$=$	$\displaystyle \int_0^xt^{\frac{1}{2}}\ \mathrm{d}t$
	↓	Integriere.
	$=$	$\displaystyle \left[\frac{2}{3}t^{\frac{3}{2}}\right]_0^x$
	↓	In die Klammer wird für $t$ der obere Wert $(x)$ eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle \left(\frac{2}{3}x^{\frac{3}{2}}\right)-\left(\frac{2}{3}0^{\frac{3}{2}}\right)$
	$=$	$\displaystyle \left(\frac{2}{3}x^{\frac{3}{2}}\right)$