1 Überblick
Inhalt des Kurses
Ziel des Kurses ist das Kennenlernen des Bruchbegriffs.
Anhand von bildlichen Darstellungen lernst du Brüche kennen, erfährst, was gemischte Brüche sind, wie sich Brüche am Zahlenstrahl darstellen lassen und welche Besonderheiten Brüche aufweisen.
Kursdauer
Der Kurs dauert ungefähr 1 Stunde.
2 Was ist ein Bruch?
Jana feiert eine Geburtstagsparty mit ihren 3 besten Freundinnen Katja, Lea und Michaela. Sie schneiden den Kuchen in 12 Stücke.

Jana isst 3 Stücke.
Diesen Anteil schreibt man als , denn es sind ja drei Zwölftel des Kuchens.
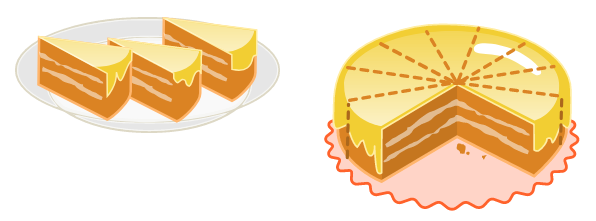
Katja isst nur 1 Stück oder . Auch Lea isst nur . Michaela isst .
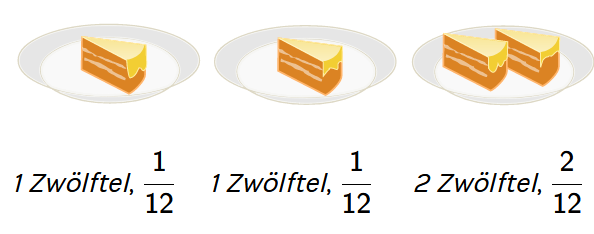
Es bleiben 5 Stücke übrig, also .

Einen solchen Anteil nennt man einen Bruch. Ein Bruch (z.B. , , ) besteht aus zwei Zahlen (Zähler und Nenner), die durch einen Bruchstrich getrennt werden.
Der Zähler (oben) gibt die Anzahl an, wie viele Stücke von allen gemeint sind.
Jana isst 3 Zwölftel. Zähler: 3
Es bleiben 5 Zwölftel übrig. Zähler: 5
Der Nenner (unten) benennt die Art der Stücke.
"Zwölftel" heißt, der Kuchen wurde in 12 gleich große Teile geteilt. Nenner: 12
Zu erledigen: Bild zu Bruch 5/12 mit Bezeichnungen Zähler, Nenner, Bruchstrich
3 Darstellung von Brüchen
Auf dieselbe Weise kannst du auch Anteile von anderen Dingen beschreiben, zum Beispiel Anteile von Kreisen oder Rechtecken
Beispiele
Der Kreis ist in 6 gleich große Teile ("Sechstel") geteilt. Der Nenner ist also 6.
Von den Sechsteln sind 2 Sechstel farbig, also ist der Zähler 2.
Dieses Bild stellt also den Bruch dar.

Das Rechteck ist in 4 gleich große Teile ("Viertel") geteilt. Der Nenner ist also 4
Von den Vierteln ist 1 Viertel farbig, also ist der Zähler 1.
Dieses Bild stellt also den Bruch dar.

Allgemein
Den Bruch bestimmt man als .
Zähle, wie viele gleich große Teile es insgesamt sind (egal ob sie farbig sind oder nicht). Dies ist der Nenner.
Zähle, wie viele der Teile farbig sind. Dies ist der Zähler.
ACHTUNG: Die Teile müssen alle gleich groß sein. Zerteile sie ansonsten, oder füge mehrere zusammen, sodass die Teile danach alle gleich groß sind.
4 Übungsaufgaben
Laden
Laden
Laden
5 Brüche auf dem Zahlenstrahl
Man kann Brüche auch auf dem Zahlenstrahl einzeichnen. Dafür zerteilt man den Zahlenstrahl zwischen 0 und 1 in gleich große Teile. Zum Beispiel in 3 Teile ("Drittel"):

Oben wurde der Bruch auf dem Zahlenstrahl eingezeichnet. Dasselbe kann man nun auch für machen:

Zeichnet man ein, so ist man bei der 1.

Auch kann man einzeichnen:

6 Video: Brüche auf dem Zahlenstrahl
Laden
7 Übungsaufgaben
Laden
Laden
8 Bruch als Division
Oft ist auch eine weitere Vorstellung zu Brüchen hilfreich: Brüche sind eine andere Schreibweise für die Division.
Beispiel
Um als Bruch darzustellen, zerteilst du ein Ganzes in 5 Teile und malst davon 3 an.

Um die Division darzustellen, zerteilst du 3 Ganze in 5 Teile.

Der rote Teil ist bei beiden Darstellungen gleich. Also ist auch
Den Bruch kannst du auch als die Division schreiben. Der Bruchstrich bedeutet also "geteilt".
9 Was ist ein gemischter Bruch?
Brüche, die größer als 1 sind, werden meistens als gemischter Bruch dargestellt.
Beispiel
Diese Schreibweise bedeutet: Man hat 3 Ganze und noch von einem weiteren Ganzen. Es ist eine Kurzform von .

Ein gemischter Bruch besteht aus einer ganzen Zahl und einem Bruch.
10 Übungsaufgaben zu gemischten Brüchen
Laden
Laden
11 Gemischten Bruch umrechnen
Du kannst eine gemischte Zahl auch in einen normalen Bruch umrechnen.

In dem Bild oben kannst du sehen, dass die 2 Ganzen in 6 Drittel zerteilt werden können. Zusammen mit dem sind es also
Einen solchen Bruch nennt man auch unechten Bruch. Der Zähler ist dann größer als der Nenner.
Vorgehen
Zuerst berechnest du, in wie viele Teile die Ganzen zerteilt werden. Multipliziere dafür die Ganzen mit dem Nenner.
Zähle danach diese Zahl und den Zähler des Bruchs zusammen. Das ist der neue Zähler des unechten Bruchs.
Der Nenner ändert sich nicht!
Beispiel:
Die 3 Ganzen werden in Teile geteilt. Insgesamt sind es also
12 Übungsaufgaben zum Umrechnen von gemischten Zahlen
in Arbeit
13 Übungsaufgaben
Welche Brüche bzw. gemischten Zahlen werden durch die Farbe blau dargestellt?


