1 Übersicht
Ziel dieses Kurses ist es, den Begriff der ganzrationalen Funktion einzuführen und den charakteristischen Verlauf des Graphen zu erarbeiten.
Inhalte
Begriffsklärung Polynomfunktion
Verhalten des Graphen im Unendlichen
Symmetrieverhalten von Polynomfunktionen
Vorwissen
Potenzfunktionen
Graphen von Potenzfunktionen
2 Begriffsklärungen (1|2)
Funktion - Potenzfunktion - ganzrationale Funktion
Funktionen
Eine Funktion ist eine Zuordnung, bei der jedem aus einer Menge genau ein aus einer Menge zugeordnet wird.
In der Mathematik geschieht dies in der Regel dadurch, dass ein Funktionsterm angegeben ist.

Potenzfunktionen
Wenn der Funktionsterm die Form hat, nennt man eine Potenzfunktion.

Graph zu

Graph zu

Graph zu
Ganzrationale Funktionen
Wenn man eine oder mehrere Potenzfunktionen zusammenaddiert, erhält man eine Polynomfunktion oder ganzrationale Funktion.

So sieht beispielsweise der Graph der Funktion aus, wenn
ist. ist eine ganzrationale Funktion, da sie aus mehreren Potenzfunktionen zusammengesetzt ist.
3 Begriffsklärungen (2|2)
Mathematische Beschreibung einer ganzrationalen Funktion
Eine ganzrationale Funktion ist definiert als eine Funktion, die sich in folgender Form schreiben lässt:
.
Dabei ist die Variable, die sind reelle Zahlen, und ist eine natürliche Zahl.
Ganzrationale Funktionen werden auch als Polynomfunktionen bezeichnet.
Noch ein paar Begriffe
Exponenten:
Die in der Definition der ganzrationalen Funktion vorkommenden hochgestellten Zahlen sind Exponenten; so bezeichnet man nämlich allgemein bei einer Potenz die hochgestellte Zahl.
Koeffizienten:
Die Zahlen nennt man Koeffizienten. (Die tief gestellten sind hier nur da, damit man die Koeffizienten auseinanderhalten kann.)
Grad einer ganzrationalen Funktion
Der größte vorkommende Exponent gibt den Grad der Polynomfunktion an.
Beispiel
Die Funktion hat den Grad .

4 Beispiele und Nicht-Beispiele
Hier findest du noch ein paar Beispiele und Nicht-Beispiele zu Polynomfunktionen.
ist eine Polynomfunktion. Allgemein sind alle quadratischen Funktionen Polynomfunktionen.
ist eine Polynomfunktion.
und sind keine Polynomfunktionen, da ein unter der Wurzel steht bzw. negative Exponenten vorkommen.
ist eine Polynomfunktion. Allgemein sind alle linearen Funktionen Polynomfunktionen.
ist keine Polynomfunktion, da die Variable im Exponenten vorkommt.
ist eine Polynomfunktion. Allgemein sind alle konstanten Funktionen Polynomfunktionen.
ist keine Polynomfunktion, da die Variable im Nenner vorkommt. Dies nennt man auch eine gebrochenrationale Funktion.
ist eine Polynomfunktion, da der Funktionsterm durch Ausmultiplizieren zu umgeformt werden kann und somit Polynomform hat.
Normalerweise schreibt man eine Polynomfunktion so auf, dass die Potenzen vom größten bis zum niedrigsten Exponent geordnet sind.
Also nicht , sondern .
5 Charakteristischer Verlauf des Graphen
Die Problemstellung
Bei Potenzfunktionen der Form kann man das ungefähre Aussehen des Graphen nach einigen Regeln aus dem Funktionsterm "vorhersagen".
Ganzrationale Funktionen (bzw. Polynomfunktionen) sind als Summe solcher Potenzfunktionen darstellbar - so sind sie ja definiert.
Gibt es auch für ganzrationale Funktionen Regeln, nach denen man das Aussehen des Graphen vorhersagen kann?
Schwer vorstellbar, dass sich hier "einfache" Regeln finden lassen….
Trotzdem: Ein paar Aussagen anhand des Terms wird man machen können.
Im Folgenden wollen wir anhand von drei "Forschungsbeispielen" versuchen, solche Regeln herauszufinden, und diese Regeln anschließend zu formulieren.
6 Erstes Forschungsbeispiel (1|2)
Einigkeit macht stark! - Beispiel 1:
Um eine Vorstellung vom Graphen von zu bekommen (ohne eigens eine Wertetabelle anzulegen und ihn zu zeichnen), zerlegen wir am besten zunächst in die beiden Potenzfunktionen, aus denen er zusammengesetzt ist:
Die Funktion sei gegeben durch:
Die Funktion sei gegeben durch:
Mit diesen Festlegungen ist dann natürlich .
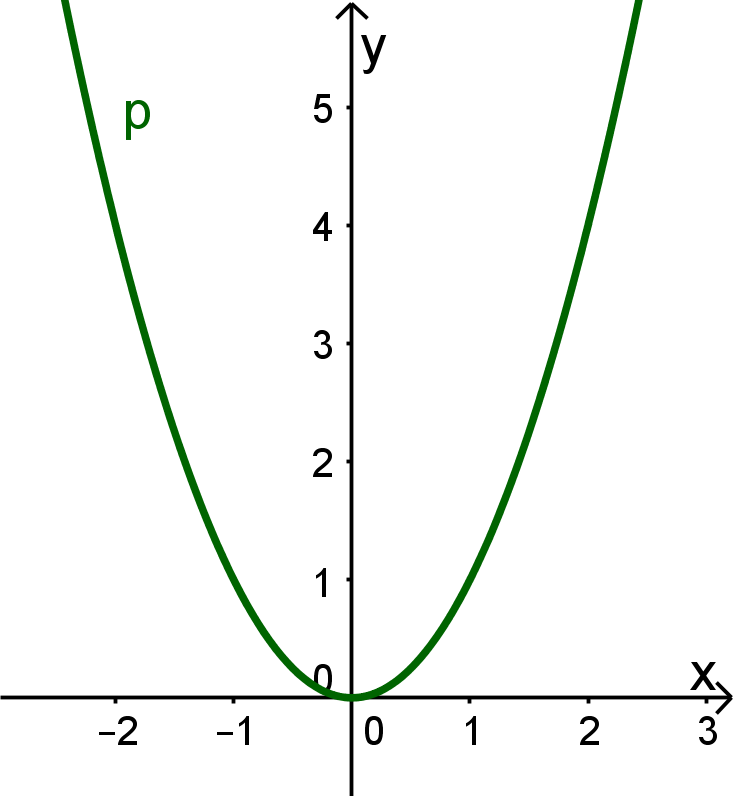
und sind Potenzfunktionen; das Verhalten ihrer Graphen kann man aus ihren Funktionstermen bereits vorhersagen, oder du liest es jetzt an den obigen Graphen ab:
Der Graph von ist
achsensymmetrisch zur -Achse und
auf beiden Seiten nach gerichtet.
Der Graph von ist
achsensymmetrisch zur -Achse und
auf beiden Seiten nach gerichtet.
Und was vermutest du nun für den Graphen von ?
Denke nach, und gehe dann zur nächsten Seite dieses Kurses …
7 Erstes Forschungsbeispiel (2|2)
Richtig; das war nicht schwer:
Auch der Graph von ist
achsensymmetrisch zur -Achse und
auf beiden Seiten nach gerichtet.
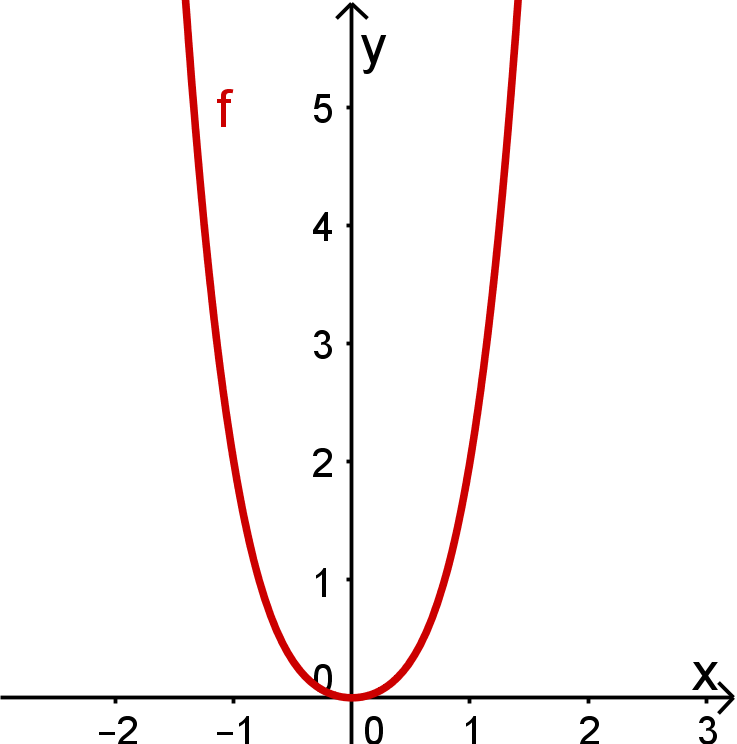
Hier siehst du eine Graphik, in der alle drei Graphen eingezeichnet sind.
Kannst du vielleicht noch weitere Beobachtungen machen, die von Bedeutung sein könnten?
Welchem der beiden ursprünglichen Graphen ähnelt der Graph von mehr, dem von oder dem von ? Was meinst du?
Nimm dir ein Blatt Papier und notiere alles, was dir wichtig erscheint - vielleicht lassen sich ja später allgemeine Regeln daraus ableiten!
8 Zweites Forschungsbeispiel (1|2)
Wer setzt sich durch? - Beispiel 2:
Auch diese Funktion zerlegen wir zunächst in zwei Potenzfunktionen und , aus denen sie zusammengesetzt ist:
Die Funktion sei gegeben durch:

Die Funktion sei gegeben durch:
Mit diesen Festlegungen ist dann auch diesmal (und nicht ).
Aber diesmal unterscheidet sich das Verhalten von und von für sehr große bzw. sehr kleine -Werte.
Was vermutest du?
Wird sich durchsetzen, und auf beiden Seiten gegen gehen?
Oder wird stärker sein, und ist auf beiden Seiten nach gerichtet?
Oder heben sich und auf, und pendelt sich irgendwie auf ein?
Oder sonst irgendetwas anderes?
Denke nach, probiere es, wenn du dir unsicher bist, aus und zeichne den Graphen - mit einer Wertetabelle oder mit einem Funktionsplotter
und schaue erst dann auf die nächste Kursseite!
9 Zweites Forschungsbeispiel (2|2)
Okay, dass der Graph von achsensymmetrisch zur -Achse sein würde, das war zu erwarten; denn schließlich sind das ja auch die Graphen von und .
Und im Unendlichen hat sich offenbar gegen durchgesetzt - jedenfalls geht der Graph auf beiden Seiten gegen .

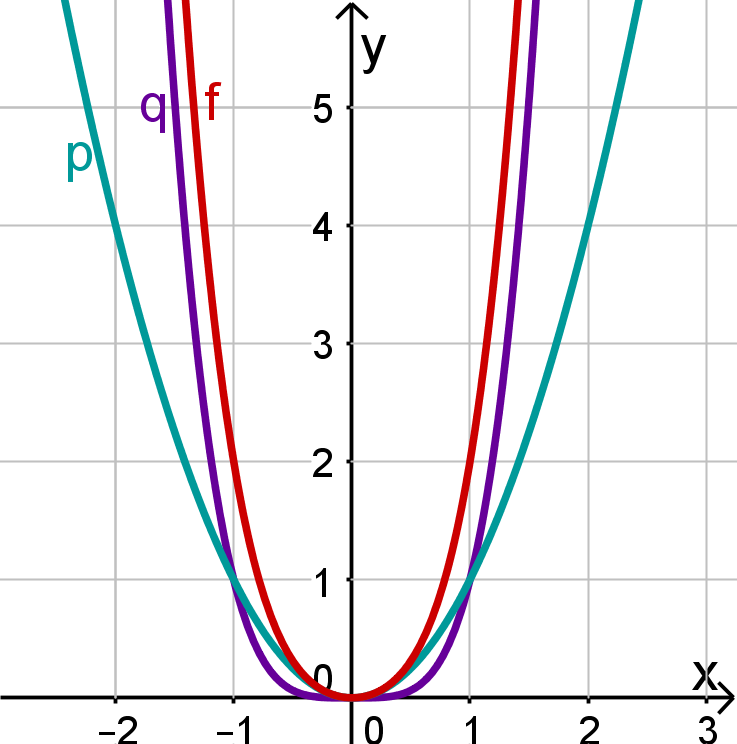
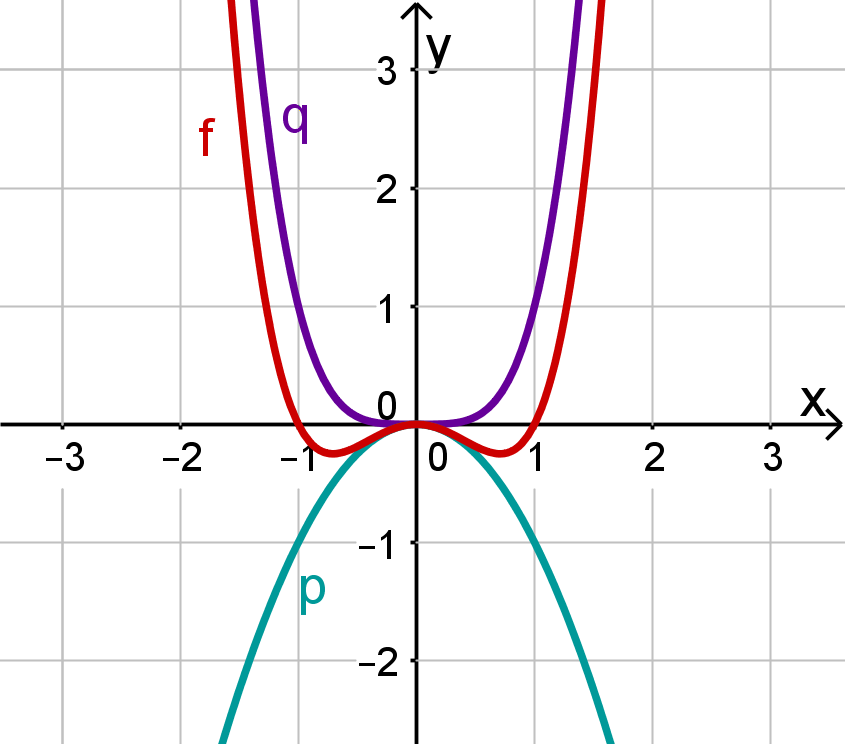
Hier siehst du eine Graphik, in der zusätzlich zum Graphen von auch die Graphen von und eingetragen sind.
Man erkennt:
Für betragsmäßig kleine -Werte (das heißt: -Werte in der Nähe der ) sieht der Graph von eher so aus wie der von ,
während
für betragsmäßig große -Werte der Einfluss von stärker ist.
10 Drittes Forschungsbeispiel (1|2)
Noch mehr verschiedene Einflüsse - Beispiel 3:
Auch diese Funktion zerlegen wir zunächst in die drei Bestandteile, aus denen sie offenkundig besteht:
 |  | 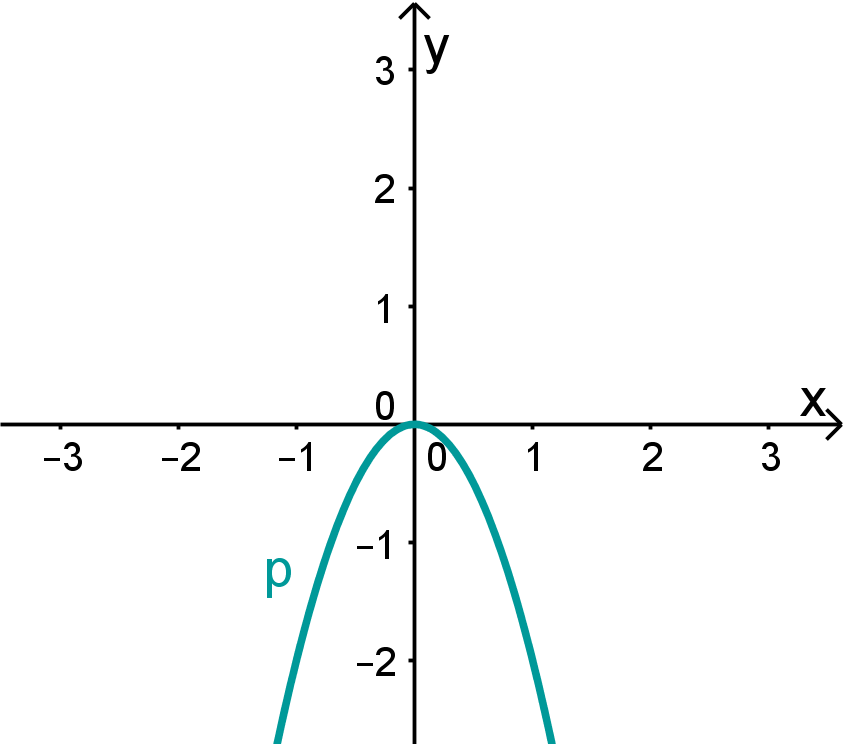 |
Der Graph von ist
| Der Graph von ist
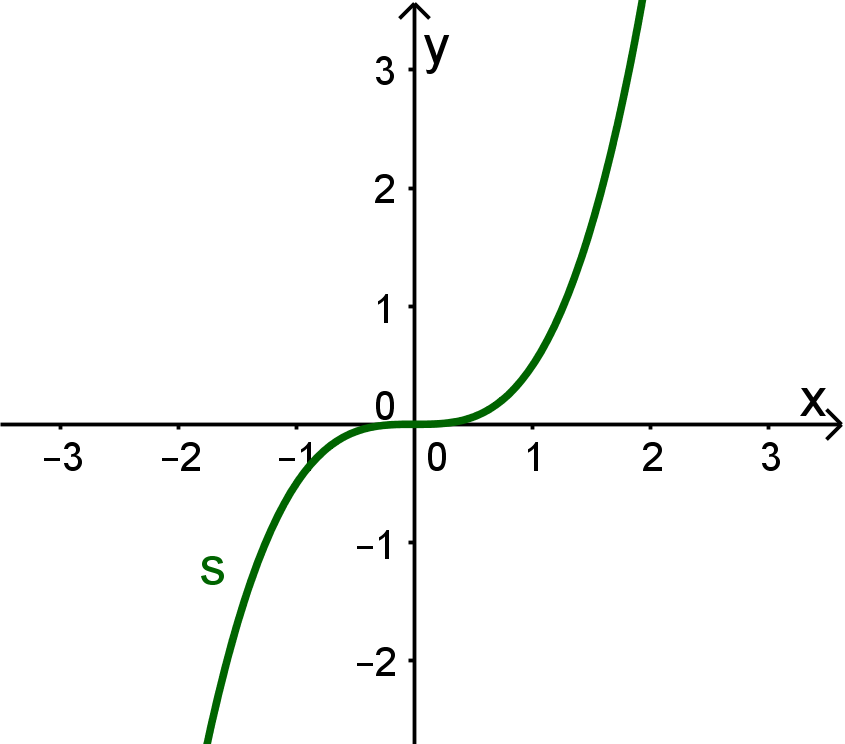
| Der Graph von ist
|
Und nun?
Was vermutest du?
Denke nach, notiere deine Überlegungen, und wenn du möchtest, probiere es einfach aus - indem du den Graphen mithilfe einer Wertetabelle oder mit einem Funktionsplotter zeichnest.
Auf der nächsten Kursseite findest du wieder die Auflösung.
11 Drittes Forschungsbeispiel (2|2)
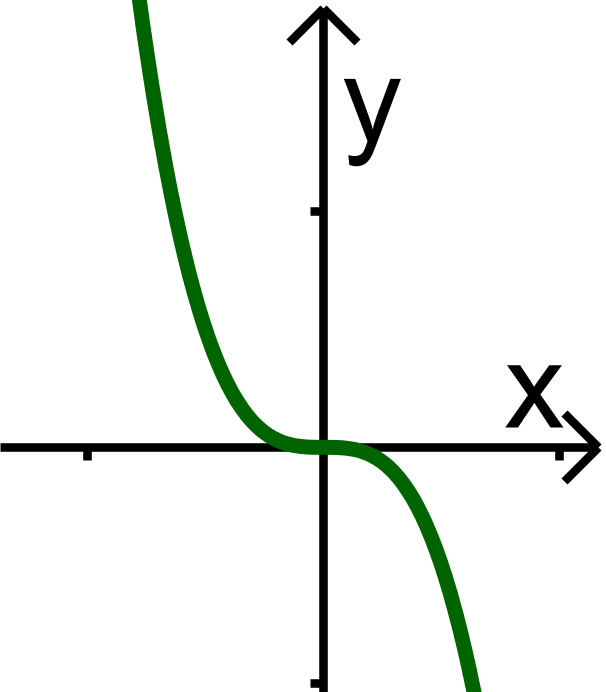
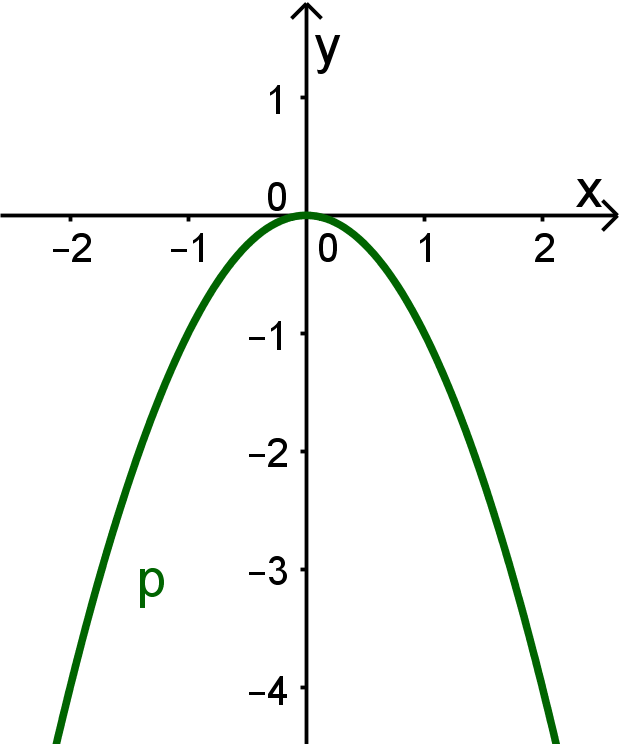
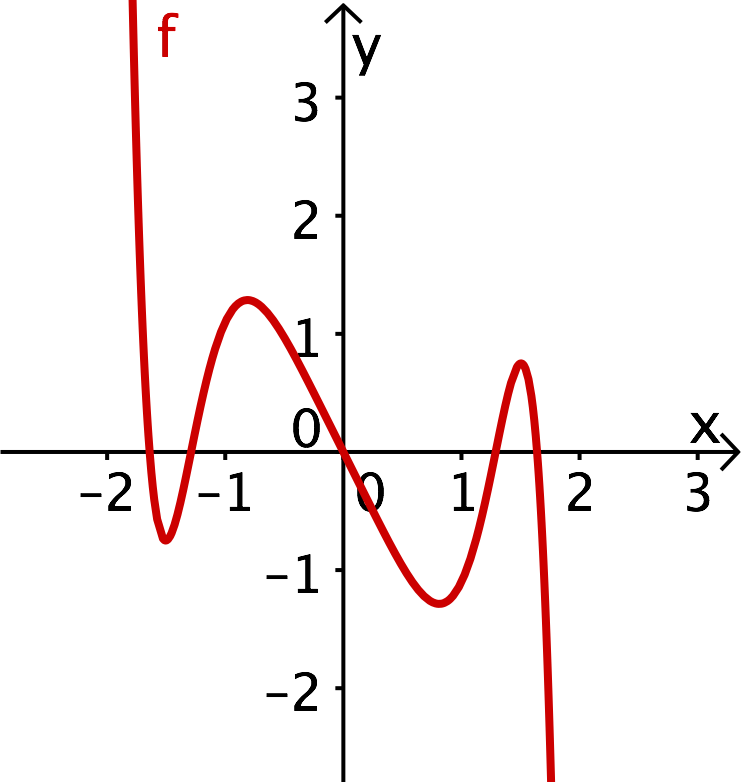
Der Graph von (siehe nebenstehendes Bild) ist
weder achsensymmetrisch zur -Achse, noch punktsymmetrisch zum Ursprung
auf beiden Seiten nach gerichtet.
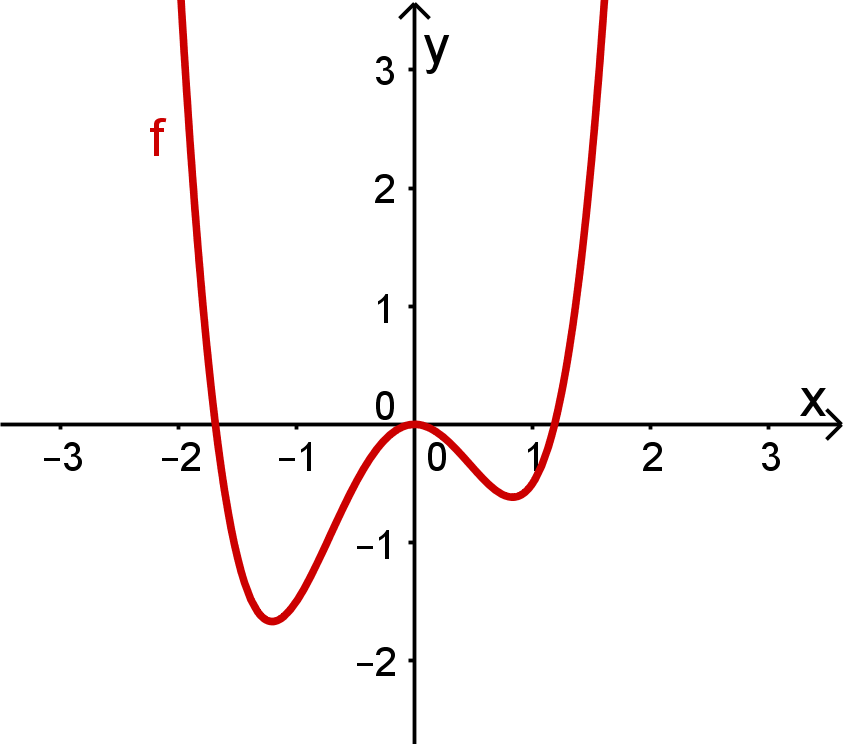
Graph der Funktion
Nun ja, Achsensymmetrie zur -Achse oder Punktsymmetrie zum Ursprung kann man wohl nicht erwarten, wenn verschieden-symmetrische Funktionen miteinander kombiniert werden.
Und im Unendlichen hat sich anscheinend wieder durchgesetzt?
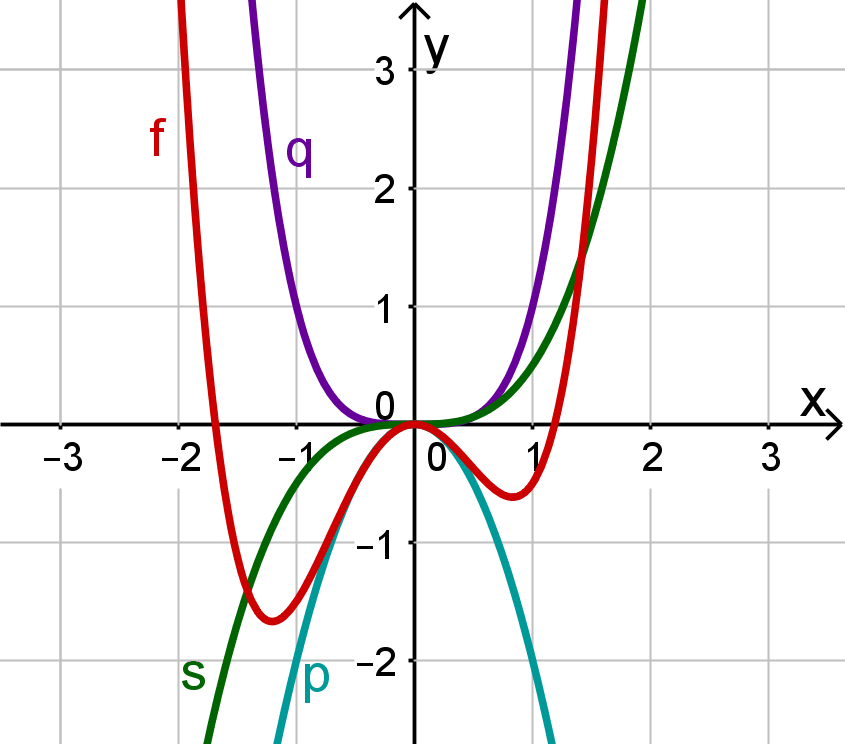
Hier in dieser Graphik sind zusätzlich zum Graphen von auch die Graphen von , und eingetragen.
Man erkennt:
Für -Werte in der Nähe der verläuft der Graph von am ehesten so wie der von .
Für betragsmäßig große -Werte ist der Graph so gerichtet, wie es dem Graphen von entspricht.
Dazwischen spielt anscheinend der Einfluss von eine deutliche Rolle.
12 Regeln - Verhalten im Unendlichen
Wie du vielleicht erkennen kannst, gibt es doch ein paar Regeln, nach denen man das Verhalten des Graphen einer Polynomfunktion vorhersagen kann.
Dazu betrachten wir abschließend alle drei Forschungsbeispiele und versuchen dabei herauszufinden, wie der Verlauf der Polynomfunktion von seinen Bestandteilen (und ) abhängt.



In allen drei Fällen nähert sich der Graph dem Graphen von für betragsmäßig große (also sehr große und sehr kleine) -Werte. Bei unseren Forschungsbeispielen war die Potenz mit dem höchsten Exponenten.
Allgemein gilt:
Für betragsmäßig große -Werte (also im Unendlichen) wird das Verhalten einer Polynomfunktion durch den Summanden mit dem höchsten vorkommenden Exponenten bestimmt.
Wie bei Potenzfunktionen gibt es nur vier Möglichkeiten für den charakteristischen Verlauf des Graphen einer ganzrationalen Funktion.
13 Regeln - Symmetrie
Symmetrie zum Koordinatensystem vorhanden
Achsensymmetrie zur -Achse
Jede ganzrationale Funktion, bei der die Variable
nur in Potenzen mit geradem Exponenten vorkommt,
ist achsensymmetrisch zur -Achse.

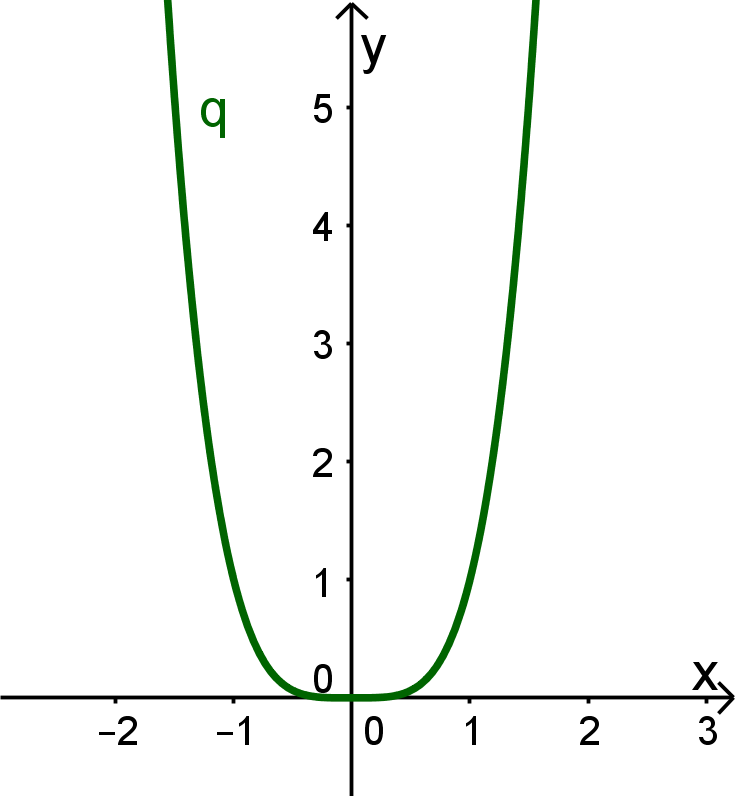
Beispiel für einen Graphen, der achsensymmetrisch zur -Achse ist.
Punktsymmetrie zum Ursprung
Jede ganzrationale Funktion, bei der die Variable
nur in Potenzen mit ungeradem Exponenten vorkommt,
ist punktsymmetrisch zum Ursprung .
Symmetrie zum Koordinatensystem nicht vorhanden
Wenn in einer ganzrationalen Funktion die Variable
als Potenz mit geradem Exponenten
und außerdem auch
als Potenz mit ungeradem Exponenten vorkommt,
ist der Graph weder achsensymmetrisch zur -Achse noch punktsymmetrisch zum Ursprung.

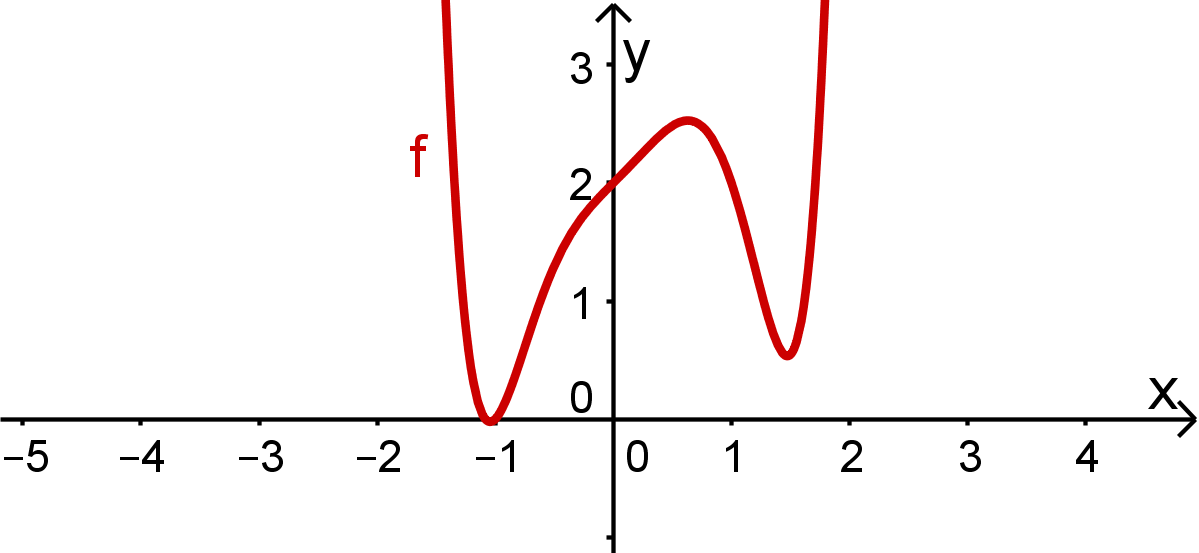
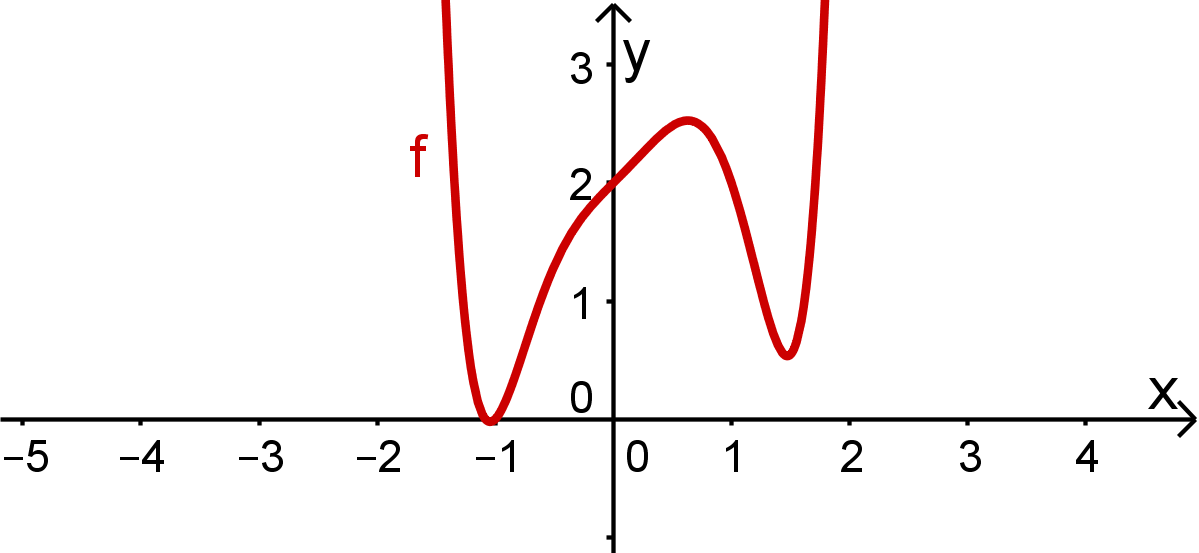
Beispiel für einen Graphen, der keine Symmetrie zum Koordinatensystem aufweist
Ob es Achsensymmetrie zu einer anderen Achse als der -Achse oder Punktsymmetrie zu einem anderen Punkt als dem Ursprung gibt, ist eine andere Frage, die schwieriger zu beantworten ist und hier nicht behandelt werden soll.
14 Aufgaben zum Verlauf des Graphen
Aufgabe 1
Laden
Aufgabe 2
Laden
Aufgabe 3
Laden
15 Zusammenfassung
Symmetrie
Wenn im Funktionsterm der ganzrationalen Funktion
nur gerade Potenzen der Variablen vorkommen, ist der Graph achsensymmetrisch zur -Achse,
nur ungerade Potenzen der Variablen vorkommen, ist der Graph punktsymmetrisch zum Ursprung,
gerade und ungerade Potenzen der Variablen vorkommen, hat der Graph keine Symmetrie zum Koordinatensystem.
Verhalten im Unendlichen
Im Unendlichen verhält sich der Graph in etwa so wie die Potenzfunktion im Funktionsterm, die den höchsten Exponenten hat.
Sonstiger Verlauf des Graphen
In der Nähe von verhält sich der Graph in etwa so wie die Potenzfunktion im Funktionsterm, die den niedrigsten Exponenten hat.
Der übrige Verlauf des Graphen wird von allen im Funktionsterm vorkommenden Termen beeinflusst; um Genaueres über ihn herauszufinden, sind zusätzliche Untersuchungen der Funktion notwendig.
Feedback
Damit wir unseren Kurs für die Zukunft verbessern können, würden wir uns sehr über ein Feedback von dir freuen. Es dauert auch nur 3 Minuten!
Klicke dazu auf diesen Link.
