Aufgaben zur Polynomfunktion - lernen mit Serlo!

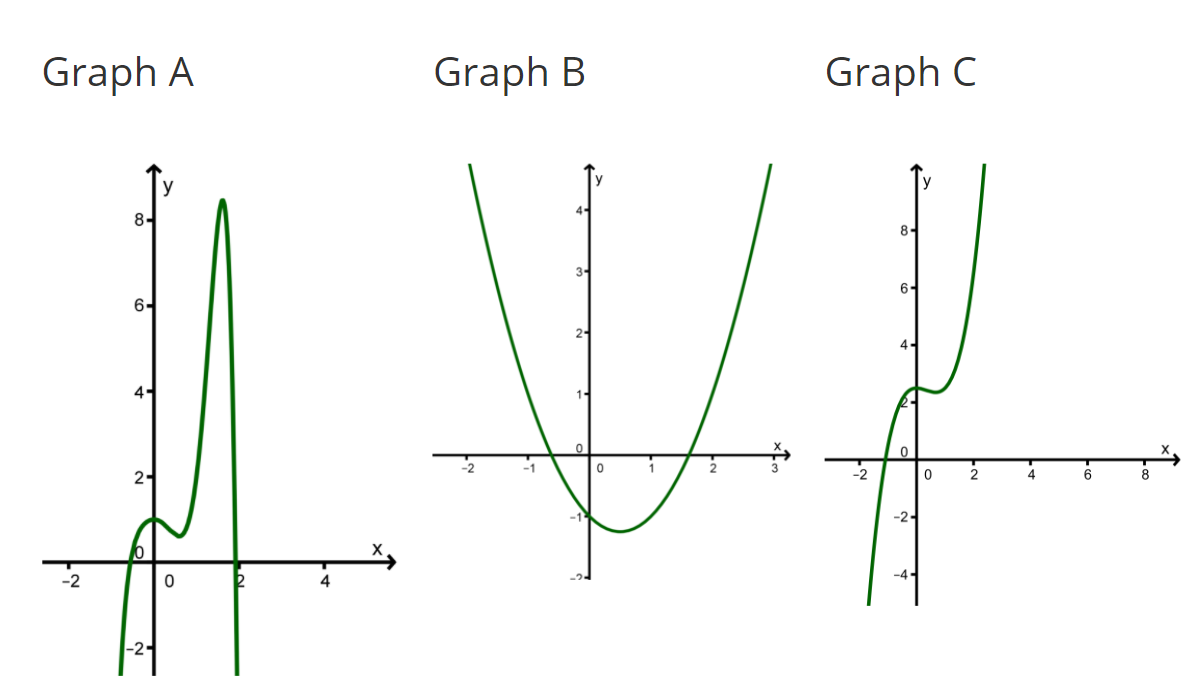
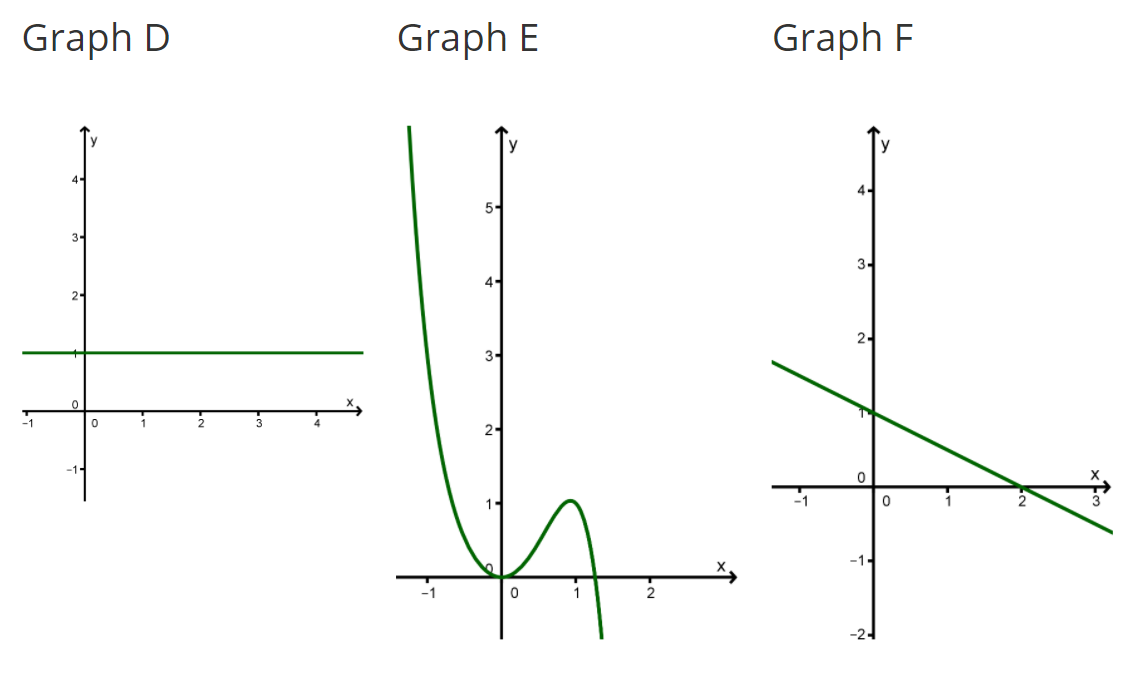
Ordne die Graphen den richtigen Funktionen zu und gib jeweils eine kurze Begründung an. Zu zwei Funktionen gibt es keinen Graphen.

$f (x) = - 0.5 x + 1$

$g (x) = - 2 x^{2}$

$h (x) = x^{2} - x - 1$

$i (x) = - 3 x^{6} + 6 x^{5} - 2 x^{2} + 1$

$k (x) = x^{3} - x^{2} + 2.5$

$l (x) = 1$

$m (x) = - x^{5} + 2 x^{2}$

$n (x) = x^{6} + x^{4}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: ganzrationale Funktionen

Eine ganzrationale Funktion ist eine Funktion, die sich aus Polynomen zusammensetzt.

Graph A

Graph A verläuft von links unten nach rechts unten.

Also muss

der höchste Exponent der zugehörigen Polynomfunktion gerade
und der zugehörige Koeffizient negativ sein.

In Frage kommen daher

Funktion $g$ mit $g (x) = - 2 x^{2}$ und
Funktion $i$ mit $i (x) = - 3 x^{6} + 6 x^{5} - 2 x^{2} + 1$ .

Funktion $g$ scheidet aus, da ihr Graph eine Parabel sein müsste.

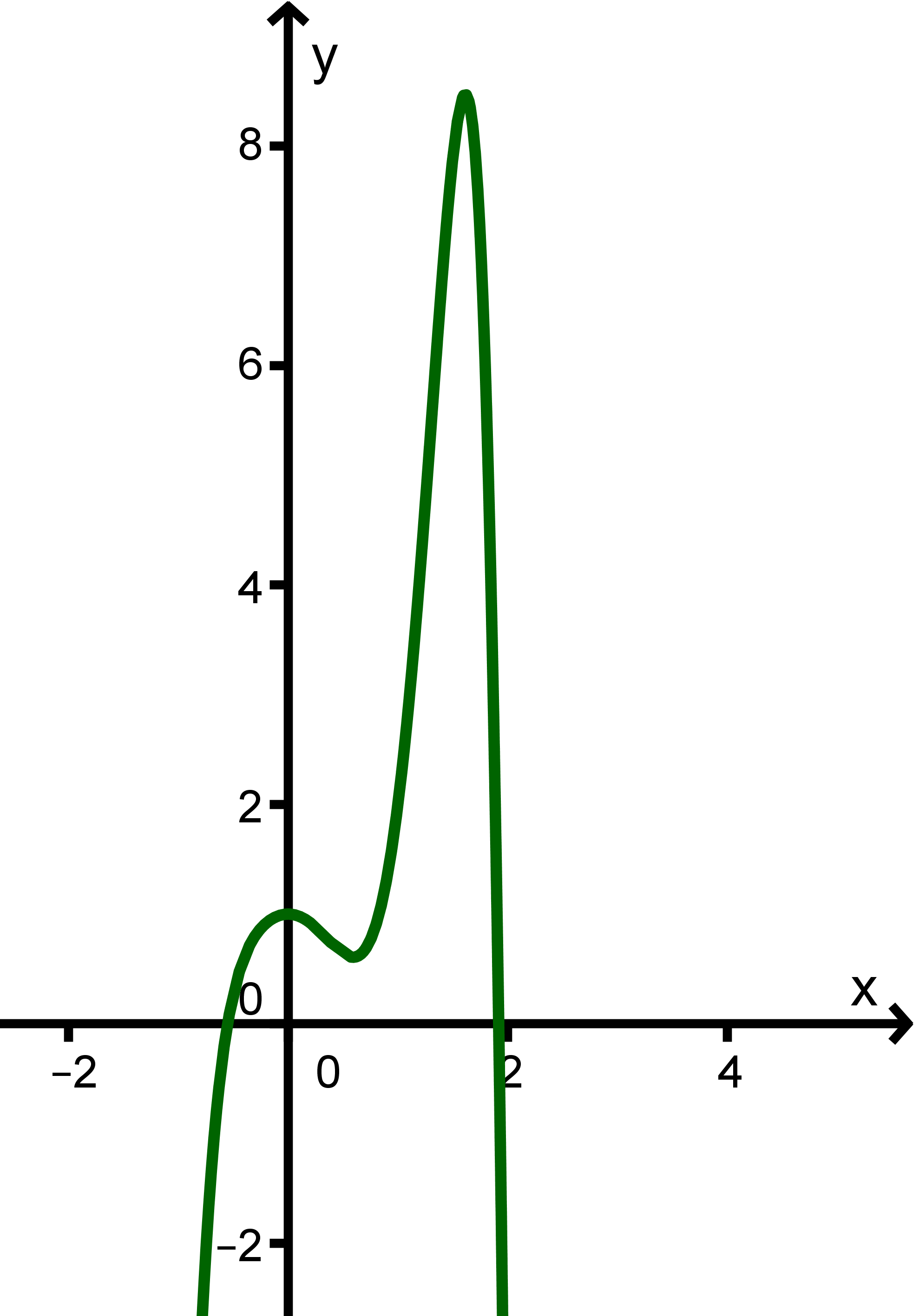
$\Rightarrow$ Ergebnis: Graph A gehört zur Funktion $i$ .

Graph B

Graph B verläuft von links oben nach rechts oben.

Also muss

der höchste Exponent der zugehörigen Polynomfunktion gerade
und der zugehörige Koeffizient positiv sein.

In Frage kommen daher:

Funktion $h$ mit $h (x) = x^{2} - x - 1$ und
Funktion $n$ mit $n (x) = x^{6} + x^{4}$ .

Um zwischen $h$ und $n$ zu unterscheiden, musst du also noch eine weitere Eigenschaft betrachten:

Der Graph von Funktion $n$ wird achsensymmetrisch zur y-Achse sein (Der Funktionsterm von $n$ enthält nur gerade Potenzen von $x$ und damit ist $f (- x) = f (x)$ ).
Der Graph von Funktion $h$ wird keine Symmetrie zur y-Achse aufweisen.

Graph B ist nicht achsensymmetrisch zur y-Achse.

Daher

kommt Funktion $n$ nicht in Frage.

$\Rightarrow$ Ergebnis: Graph B gehört zur Funktion $h$ .

Graph C

Graph C verläuft von links unten nach rechts oben.

Also muss

der höchste Exponent der zugehörigen Polynomfunktion ungerade
und der zugehörige Koeffizient positiv sein.

In Frage kommt daher nur:

Funktion $k$ mit $k (x) = x^{3} - x^{2} + 2.5$

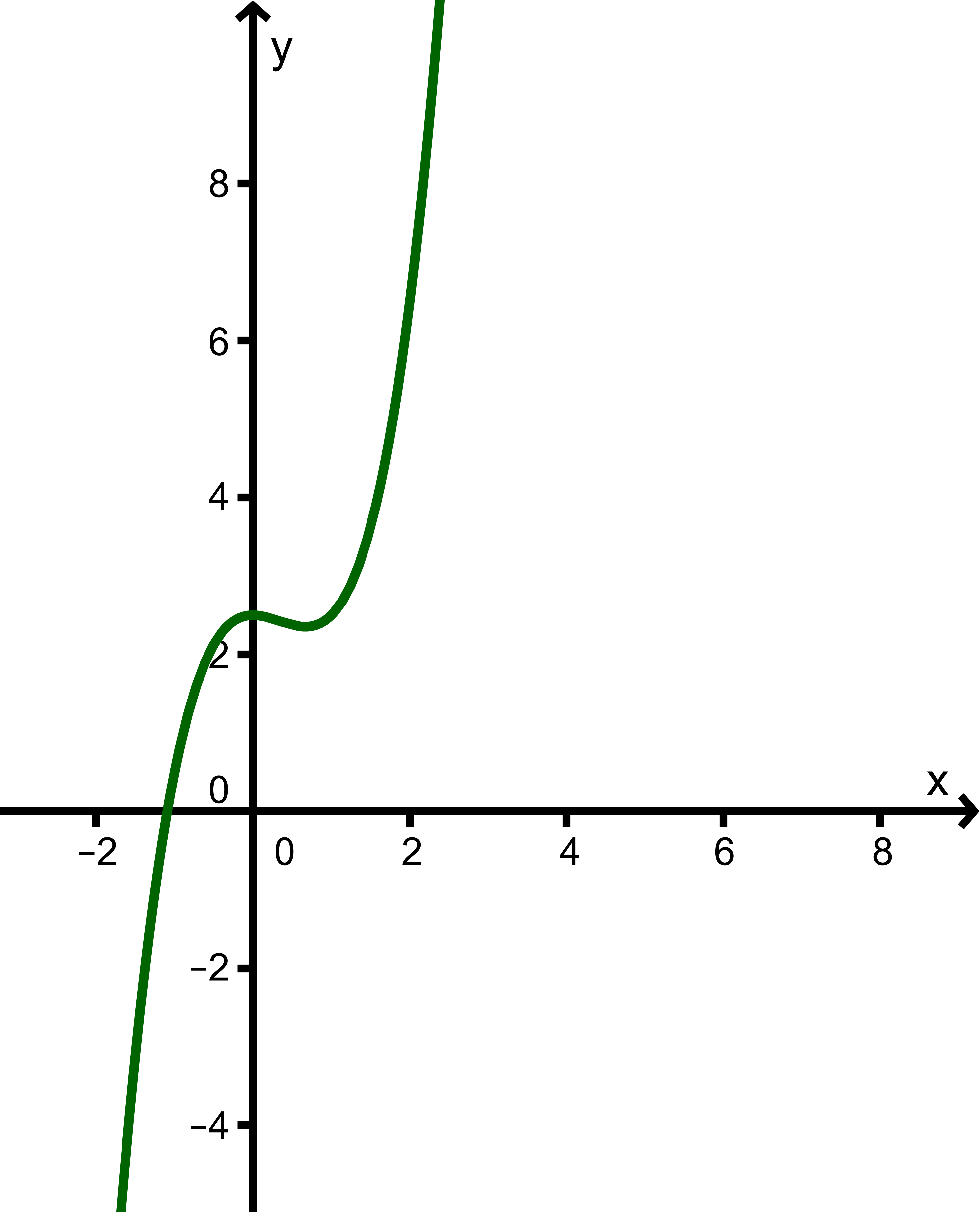
$\Rightarrow$ Ergebnis: Graph C gehört zur Funktion $k$ .

Graph D

Graph D gehört zu einer konstanten Funktion.

In Frage kommt daher nur:

Funktion $l$ mit $l (x) = 1$

$\Rightarrow$ Ergebnis: Graph D gehört zur Funktion $l$ .

Graph E

Graph E verläuft von links oben nach rechts unten.

Also muss

der höchste Exponent der zugehörigen Polynomfunktion ungerade
und der zugehörige Koeffizient negativ sein.

In Frage kommen daher:

Funktion $f$ mit $f (x) = - 0.5 x + 1$ und
Funktion $m$ mit $m (x) = - x^{5} + 2 x^{2}$ .

Funktion $f$ scheidet aber aus, da sie eine lineare Funktion ist und deshalb ihr Graph eine Gerade sein müsste.

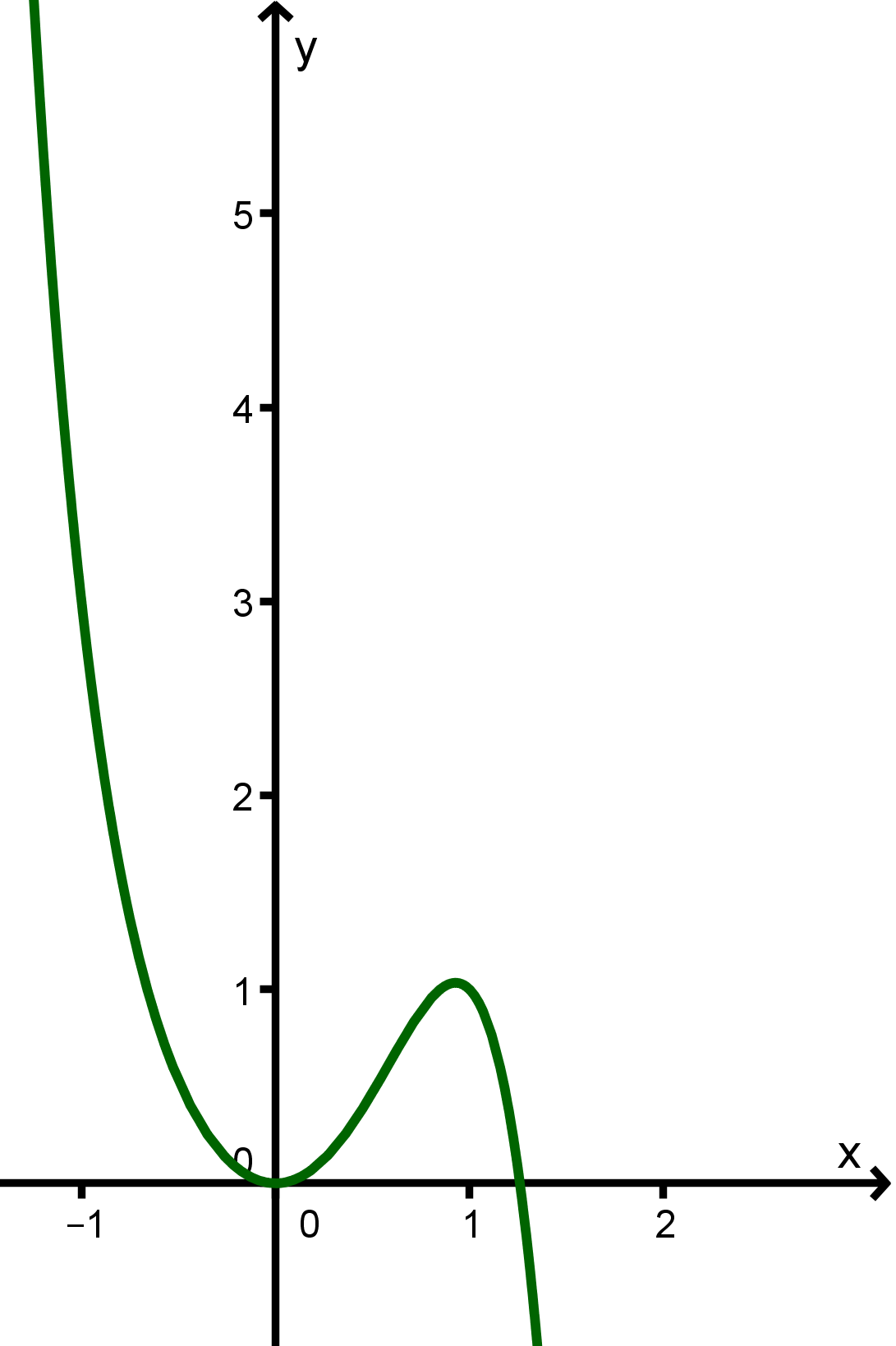
$\Rightarrow$ Ergebnis: Graph E gehört zur Funktion $m$ .

Graph F

Graph F verläuft von links oben nach rechts unten.

Also muss

der höchste Exponent der zugehörigen Polynomfunktion ungerade
und der zugehörige Koeffizient negativ sein.

In Frage kämen daher wieder $f$ und $m$ . Aber du erkennst leicht:

Graph F ist eine Gerade.

Also muss die zu Graph F gehörende Funktion linear sein; das heißt, dass ihre Funktionsgleichung die Form $y = m x + t$ haben muss.

In Frage kommt daher nur:

Funktion $f$ mit $f (x) = - 0.5 x + 1$

$\Rightarrow$ Ergebnis: Graph F gehört zur Funktion $f$ .

Zusammenfassung:

Graph A: $i$ Graph B: $h$ Graph C: $k$ Graph D: $l$ Graph E: $m$ Graph F: $f$

keinen passenden Graphen: $g$ und $n$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?