1 Übersicht
Inhalt des Kurses:
In diesem Kurs lernst du die grundlegenden Eigenschaften einer Ebene im dreidimensionalen Raum.
Vorkenntnisse:
Du solltest verstanden haben was für Eigenschaften ein Vektor und eine Gerade im Raum haben und dich im dreidimensionalen Koordinatensystem zurecht finden.
Kursdauer:
Der Kurs dauert ungefähr 2 Stunden.
2 Was ist eine Ebene?
Bisher kennst du nur eine Gerade; in der dreidimensionalen Geometrie gibt es jedoch noch den Begriff der Ebene.
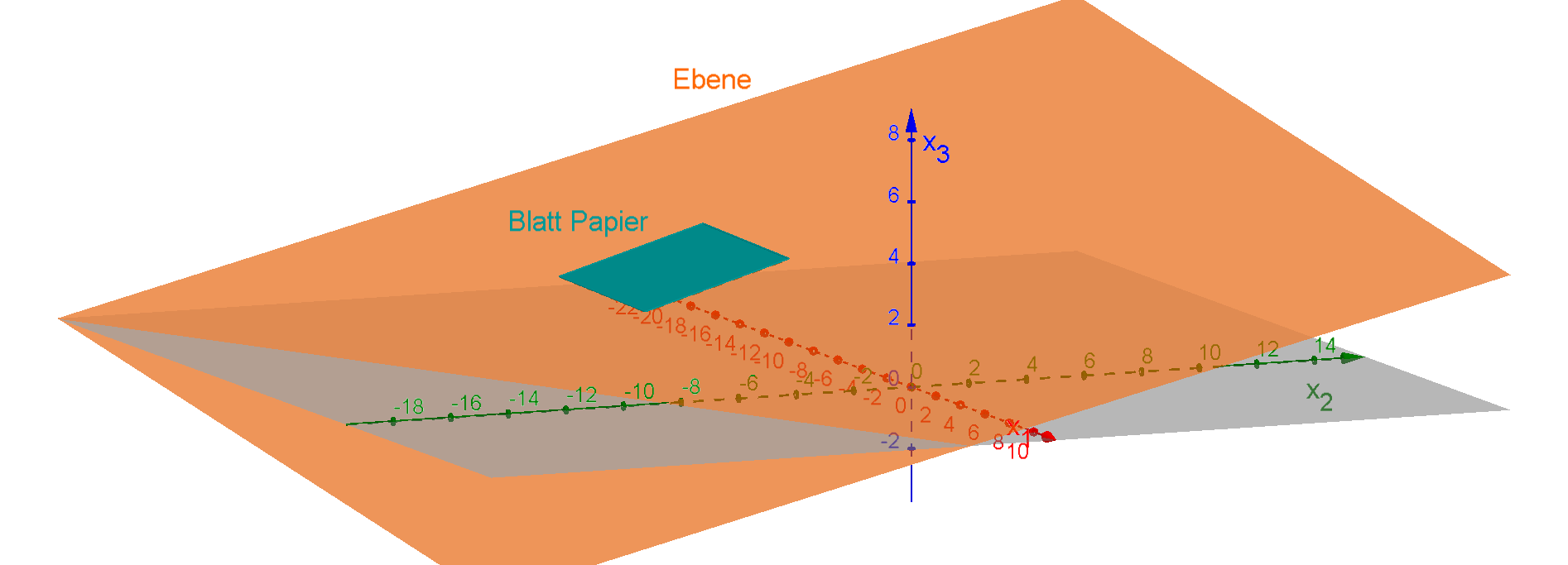
Möchtest du dir eine Ebene vereinfacht und anschaulich vorstellen, kannst du dir ein Blatt Papier nehmen und dieses in die Luft halten. Die Fläche des Papiers kannst du dir als Ebene vorstellen, das heißt jeder Punkt den du auf dein Blatt Papier malst, liegt in der Ebene.
Möchtest du das Beispiel mit dem Blatt Papier nun auf die dreidimensionale Geometrie übertragen, musst du nicht viele Eigenschaften ergänzen. In der Geometrie ist eine Ebene genauso wie dein Blatt Papier ein flaches Objekt.Der Unterschied zu deinem Blatt Papier ist, dass eine Ebene unendlich groß ist, wodurch sie wie eine Gerade keinen Anfang und kein Ende hat.
3 Bewegung in einer Ebene
Du hast dir einen Rasenmähroboter gekauft. Dieser kann nur in vier verschiedene Richtungen gesteuert werden: geradeaus, rückwärts, nach links und nach rechts.

Du baust die Ladestation auf und setzt anschließend den Mähroboter auf einen beliebigen Punkt in deinem Garten. Kannst du deinen Mähroboter zur Ladestation steuern, egal, von welchem Punkt im Garten du startest?
In dem untenstehenden Applet kannst du versuchen, den Rasenmähroboter von verschiedenen Startpunkten aus zur Ladestation zu bewegen. Der Rasenmähroboter ist der rote Punkt, die Ladestation ist der lila Punkt.
4 Bewegung in einer schrägen Ebene
Dein Nachbar besitzt einen Garten in Hanglage. Er fragt dich, ob du ihm deinen Rasenmähroboter ausleihen möchtest. Kannst du den Rasenmähroboter auch auf einem Hang zu jedem beliebigen Punkt steuern?

Auflösung: Ja. So lange man auf einer Ebene bleibt, kann man sich auf ihr bewegen wie in einer nicht-schrägen Ebene, also einer Ebene, die parallel zur -Ebene liegt. Das kann man mit Vektoren beschreiben. Mit einer Linearkombination zweier Vektoren, die sich in Länge und Richtung unterscheiden, kann man jeden Punkt auf einer Ebene erreichen.
5 Ebenengleichung aufstellen
Wenn du dein Blatt Papier irgendwo fest drauflegen willst, reicht dir ein Punkt nicht aus: Dein Blatt würde herunterfallen. Dasselbe passiert dir noch bei zwei Punkten, das Papier kippt seitlich herunter.
Bei drei Punkten liegt das Blatt Papier fest in einer Position. Alternativ kannst du dein Blatt auch auf zwei Leisten legen, oder auf eine Punkthalterung und eine Leiste, ohne dass das Blatt herunterfällt.
Das Prinzip kann man von einem Blatt Papier eins zu eins auf die Ebenen in der Geometrie übertragen.
Die türkisen Punkte kannst du bewegen um zu sehen wie die Ebene verdreht werden kann, wenn nicht drei festgelegte Punkte da sind.
6 Ebene aufstellen mit einer Gerade und einem Punkt
Du hattest dir bereits mit dem Blatt Papier überlegt, was du brauchst, um eine Ebene zu stützen. Eine der Möglichkeiten ist, die Ebene mit einem Punkt und einer Gerade zu stützen. Möchtest du also die Ebenengleichung aufstellen, kennst du bereits die Gleichung einer Gerade, zum Beispiel eine Gerade mit einem Aufpunkt und einem Richtungsvektor :
Auf der Gerade kannst du dich bereits vor und zurückbewegen und zwar in Richtung deines Richtungsvektors . Möchtest du jedoch wie in dem Rasenmähroboter-Beispiel alle Punkte in der Ebene erreichen, brauchst du noch eine zweite Richtung, in die du dich bewegen kannst und zwar in Richtung des Punktes , denn dieser soll auch in der Ebene liegen. Dazu stellst du den Verbindungsvektor zwischen dem Punkt und dem Aufpunkt der Geraden auf. Dann addierst du , mit einer Variable multipliziert, zu der Gleichung der Geraden hinzu und erhältst die Ebenengleichung der Ebene .
Wenn du den Verbindungsvektor zwischen dem Aufpunkt und dem Punkt aufstellst, musst du beachten, dass dieser nicht linear abhängig zu dem Richtungsvektor ist. Das bedeutet, einfach gesagt, dass der Punkt nicht auf der Gerade liegen darf, denn sonst erhältst du keine neue Richtung, in die du gehen kannst.
7 Beispiel: Ebene aufstellen mit einem Punkt und einer Gerade
Stelle die Gleichung für die Ebene auf, die durch den Punkt und die Gerade
läuft. Den Aufpunkt der Geraden kannst du bereits als den Aufpunkt der Ebene nehmen. Auch den Richtungsvektor der Geraden kannst du bereits direkt als Spannvektor der Ebene verwenden. Um eine zweite Richtung zu erhalten, stellst du den Verbindungsvektor zwischen dem Punkt und dem Aufpunkt der Gerade auf. Dem Verbindungsvektor kannst du eine Variable deiner Wahl zuordnen, hier im folgendem heißt er :
Nun hast du deine zwei Richtungen und kannst die Ebenegleichung für aufstellen:
8 Ebene aufstellen mit 3 Punkten
Möchtest du eine Ebenengleichung für eine Ebene durch drei Punkte und aufstellen, wählst du einen der Punkte als Aufpunkt. Dieser entspricht dem Startpunkt aus dem Beispiel, an den du deinen Rasenmähroboter zu Beginn in den Rasen gesetzt hast.
Um jeden Punkt in der Ebene zu erreichen, brauchst du wieder zwei Richtungsvektoren. Nachdem alle drei Punkte in der Ebene liegen sollen, willst du von deinem Aufpunkt aus alle drei Punkte erreichen können. Du nimmst also als Richtungsvektoren die Verbindungsvektoren zwischen dem Aufpunkt und den anderen beiden Punkten. Würdest du zum Beispiel als Aufpunkt wählen, müsstest du die Verbindungsvektoren und aufstellen.
Die beiden Richtungsvektoren addierst du dann, jeweils multipliziert mit einer von einander unterschiedlichen Variable, zu dem Aufpunkt dazu und erhälst eine Ebenengleichung.
Genauso wie zuvor, müssen die beiden Verbindungsvektoren linear unabhängig sein. Das heißt, dass die drei Punkte nicht auf einer gemeinsamen Gerade liegen dürfen.
9 Beispiel: Ebene durch 3 Punkte
Stelle die Gleichung einer Ebene auf, die durch die Punkte , , geht:
Wähle als Aufpunkt den Punkt und stelle die Verbindungsvektoren und auf.
Stelle die Ebenengleichung mit den beiden Verbindungsvektoren als Richtungsvektoren für die Ebene auf:
10 Ebene mit zwei Geraden aufstellen
Um eine Ebenengleichung aus zwei Geraden zu erstellen, müssen diese bestimmte Bedingungen erfüllen. Sie müssen entweder parallel sein oder sich schneiden. Windschiefe Geraden können keine Ebene erzeugen. Die allgemeine Form der Gleichung lautet:
wobei und die Richtungsvektoren sind
Um eine Ebenengleichung zu erstellen, wählt man sich auf einer der beiden Geraden einen Aufpunkt und nimmt den Richtungsvektor der Geradengleichung als ersten Spannvektor der Ebene.
Schneiden sich die beiden Geraden, kann man einfach den Richtungsvektor der zweiten Geradengleichung als zweiten Spannvektor der Ebene verwenden.
Sind die beiden Geraden parallel, erstellt man einen neuen Richtungsvektor, den man aus dem Aufpunkt und einem Punkt auf der zweiten Geraden erstellt. Diesen Vektor nimmt man nun als zweiten Spannvektor für die Ebene.
11 Beispiel: Ebene mit zwei sich schneidenden Geraden aufstellen
Gegeben sind zwei sich schneidende Geraden (siehe Spoiler)
Prüfe nun, ob die beiden Geraden parallel zueinander sind.
Da kein Vielfaches von ist, sind die beiden Geraden nicht parallel.
Deshalb kannst du nun einfach als Aufpunkt der Ebene den Aufpunkt der Geraden wählen. Der erste Spannvektor von ist der Richtungsvektor der Geraden und der zweite Spannvektor ist der Richtungsvektor der Geraden .
Also lautet die Ebenengleichung:
12 Zusammenfassung
Vergleichst du alle drei Möglichkeiten eine Ebenengleichung aufzustellen, stellst du fest: Du hast immer einen Aufpunk und gehst von diesem aus in zwei Richtungen und .
Du erhälst also eine allgemeine Ebenengleichung für eine Ebene wie folgt:
Mit den beiden Vektoren und erreichst du von aus jeden Punkt der Ebene .
Die Vektoren und erhälst du entweder durch das Aufstellen von Verbindungsvektoren oder wenn du gegebene Vektoren von Geraden nutzt. Wichtig ist nur, dass die beiden Vektoren immer linearunabhängig zueinander sein müssen.
Diese Schreibweise der Ebene nennt man Parameterform einer Ebene.
13 Aufgaben
Laden
Laden
Stelle aus einem Punkt und zwei Richtungsvektoren eine Ebenengleichung in Parameterform auf:
Laden
Stelle aus den folgenden drei Punkten eine Ebenengleichung in Parameterform auf:
Laden
